
Giải chi tiết Giải SGK Toán 9 Bài 4 (Sách Cánh diều): Góc ở tâm. Góc nội tiếp – SÁCH GIÁO KHOA TOÁN 9 CÁNH DIỀU – 2024
================
Giải bài tập Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp
Khởi động trang 111 Toán 9 Tập 1:Bác Ngọc dự định làm khung sắt cho khuôn cửa sổ ngôi nhà có dạng đường tròn nhưHình 44. Hai thanh chắn cửa sổ gợi nên một góc có đỉnh thuộc đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Góc có đặc điểm như vậy trong toán học gọi là góc gì?
Lời giải:
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Góc có đỉnh thuộc đường tròn và hai cạnh chứa hai dây cung của đường tròn đó được gọi là góc nội tiếp.
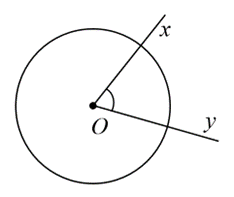
Hoạt động 1 trang 111 Toán 9 Tập 1:Cho đường tròn (O). Hãy vẽ góc xOy có đỉnh là tâm O của đường tròn đó.
Lời giải:
Hình vẽ góc xOy có đỉnh là tâm O của đường tròn (O) như sau:
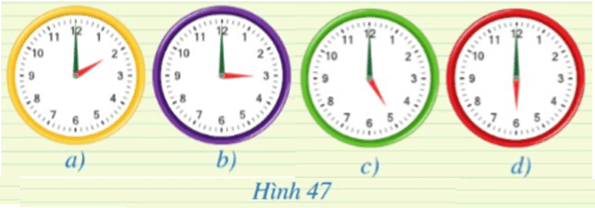
Luyện tập 1 trang 111 Toán 9 Tập 1:TrongHình 47, coi mỗi khung đồng hồ là một đường tròn, kim giờ, kim phút là các tia. Số đo góc ở tâm trong mỗi hình 47a, 47b, 47c, 47d là bao nhiêu?
Lời giải:
a) Số đo góc ở tâm là 60°.
b) Số đo góc ở tâm là 90°.
c) Số đo góc ở tâm là 150°.
d) Số đo góc ở tâm là 180°.
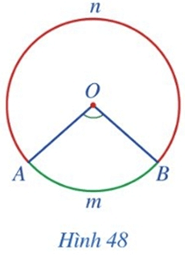
Hoạt động 2 trang 112 Toán 9 Tập 1:Quan sát góc ở tâm AOB (khác góc bẹt) ởHình 48, cho biết trong hai phần đường tròn được tô màu xanh và màu đỏ, phần nào nằm bên trong, phần nào nằm bên ngoài góc AOB.
Lời giải:
Phần đường tròn được tô màu xanh nằm bên trong góc AOB.
Phần đường tròn được tô màu đỏ nằm bên ngoài góc AOB.
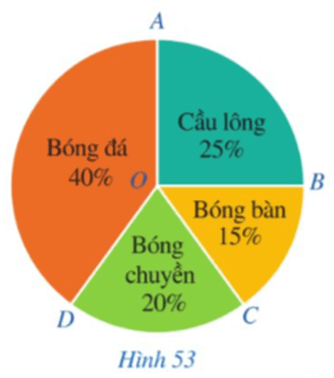
Luyện tập 2 trang 114 Toán 9 Tập 1:TrongHình 53, tìm số đo của các góc ở tâm
Lời giải:
⦁ Do số học sinh chọn môn Bóng bàn chiếm 15% số lượng học sinh nên số đo cung nhỏ BC bằng 15% số đo của cung cả đường tròn. Vì thế,
Vì số đo của cung nhỏ BC bằng số đo của góc ở tâm BOC chắn cung đó nên
⦁ Do số học sinh chọn môn Bóng đá chiếm 40% số lượng học sinh nên số đo cung nhỏ DA bằng 40% số đo của cung cả đường tròn. Vì thế,
Vì số đo của cung nhỏ DA bằng số đo của góc ở tâm DOA chắn cung đó nên
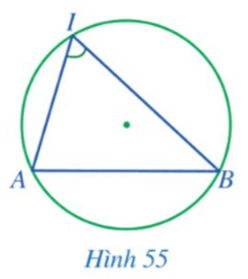
Hoạt động 3 trang 115 Toán 9 Tập 1:TrongHình 55, đỉnh của góc AIB có thuộc đường tròn hay không? Hai cạnh của góc chứa hai dây cung nào của đường tròn?
Lời giải:
⦁ Đỉnh của góc AIB là điểm I, điểm I có thuộc đường tròn.
⦁ Hai cạnh của góc AIB chứa hai dây cung IA, IB của đường tròn.
Luyện tập 3 trang 115 Toán 9 Tập 1:Hãy vẽ một đường tròn và hai góc nội tiếp trong đường tròn đó.
Lời giải:

là hai góc nội tiếp đường tròn (O).
Hoạt động 4 trang 115 Toán 9 Tập 1:Cho góc AIB nội tiếp đường tròn tâm O đường kính IK sao cho tâm O nằm trong góc đó (Hình 57).
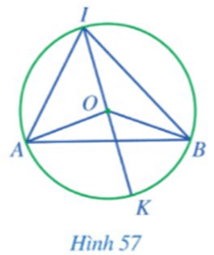
a) Các cặp gócvà;vàcó bằng nhau hay không?
b) Tính các tổng
c) Tính các tổng
d) So sánhvà,vàvà.
Lời giải:
a) Xét ∆OAI có OA = OI nên ∆OAI cân tại O, suy ra
Xét ∆OBI có OB = OI nên ∆OBI cân tại O, suy ra
b) Xét ∆OAI có(định lí tổng các góc của một tam giác).
Do đó
Xét ∆OBI có(định lí tổng các góc của một tam giác).
Do đó
c)(các cặp góc kề bù).
d) Ta có(theo câu b) và(theo câu c)
Suy ra
Ta có(theo câu b) và(theo câu c)
Suy ra
Ta có:và
Suy ra
Do đó
Luyện tập 4 trang 116 Toán 9 Tập 1:Cho đường tròn (O; R) và dây cung AB = R. Điểm C thuộc cung lớn AB, C khác A và B. Tính số đo góc ACB.
Lời giải:
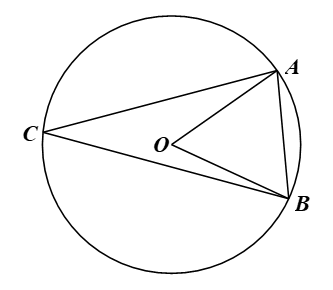
Xét ∆AOB có: OA = OB = AB = R nên ∆AOB là tam giác đều, do đó
Màlà góc ở tâm vàlà góc nội tiếp cùng chắn cung AB của đường tròn (O). Do đó
Vậy
Hoạt động 5 trang 116 Toán 9 Tập 1:Quan sátHình 60và nêu mối liên hệ giữa:
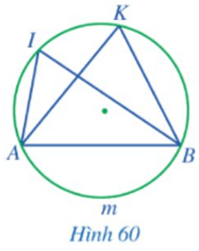
a)và
b)và
c)và
Lời giải:
a) Ta cóvàlần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AmB của đường tròn (O) nên
b) Ta cóvàlần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AmB của đường tròn (O) nên
c) Ta có:(theo câu a) và(theo câu b)
Do đó
Luyện tập 5 trang 117 Toán 9 Tập 1:TrongHình 61, gọi I là giao điểm của AD và BC. Chứng minh IA.ID = IB.IC.
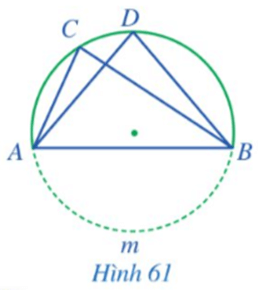
Lời giải:
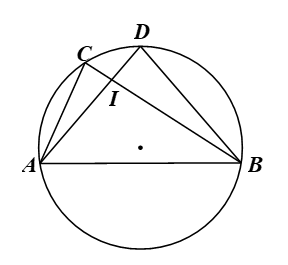
Xét đường tròn chứa cung AB ta có:là hai góc nội tiếp cùng chắn cung AB nên
Xét ∆AIC và ∆BID có:
(do
(hai góc đối đỉnh).
Do đó ∆AIC ᔕ ∆BID (g.g).
Suy ra(tỉ số các cạnh tương ứng) nên IA.ID = IB.IC.
Bài tập
Bài 1 trang 117 Toán 9 Tập 1:Quan sátHình 62,hãy cho biết:
a) 6 góc ở tâm có hai cạnh lần lượt chứa hai điểm trong bốn điểm A, B, C, D;
b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm A, B, C, D.
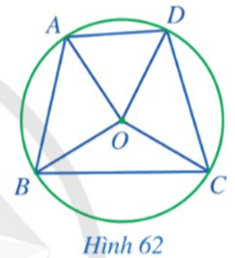
Lời giải:
a) 6 góc ở tâm có hai cạnh lần lượt chứa hai điểm trong bốn điểm A, B, C, D là các góc:
b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm A, B, C, D là các góc:
Bài 2 trang 117 Toán 9 Tập 1:Cho đường tròn (O; R) và dây AB sao choGiả sử M, N lần lượt là các điểm thuộc cung lớn AB và cung nhỏ AB (M, N khác A và B).
a) Tính độ dài đoạn thẳng AB theo R.
b) Tính số đo các góc ANB và AMB.
Lời giải:
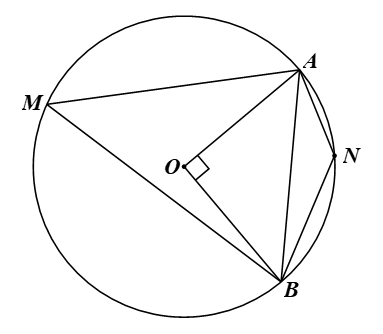
a) Xét đường tròn (O: R) có A, B thuộc đường tròn nên OA = OB = R.
Xét ∆AOB vuông tại O, theo định lí Pythagore, ta có:
AB2= OA2+ OB2= R2+ R2= 2R2.
Do đó: AB =
b) Xét đường tròn (O) cólà góc ở tâm chắn cung ANB nên
Ta có:
Vìlà góc nội tiếp chắn cung AMB nên
Vìlà góc nội tiếp chắn cung ANB nên
Bài 3 trang 117 Toán 9 Tập 1:TrongHình 63, cho biết AB = OA.
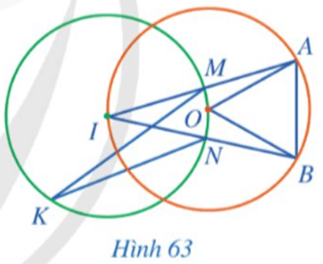
a) Tính số đo góc AOB.
b) Tính số đo cung nhỏ AB và cung lớn AB của (O).
c) Tính số đo góc MIN.
d) Tính số đo cung nhỏ MN và cung lớn MN của (I).
e) Tính số đo góc MKN.
Lời giải:
a) Xét ∆OAB có OA = OB = AB nên ∆OAB là tam giác đều, do đó
b) Số đo cung nhỏ AB là:
Số đo cung lớn AB (cung AIB) là:
c) Góc MIN hay chính là góc AIB là góc nội tiếp chắn cung nhỏ AB nên
d) Xét đường tròn (I) có góc MIN là góc ở tâm chắn cung nhỏ MN (cung MON) nên số đo cung nhỏ MN là
Số đo cung lớnMN (cung MKN) là:
e) Xét đường tròn (I) có góc MKN là góc nội tiếp chắn cung nhỏ MN nên
Bài 4 trang 117 Toán 9 Tập 1:Biểu đồ hình quạt tròn ởHình 64mô tả các thành phần của một chai nước ép hoa quả (tính theo tỉ số phần trăm). Hãy cho biết các cung tương ứng với phần biểu diễn thành phần việt quất, táo, mật ong lần lượt có số đo là bao nhiêu độ.
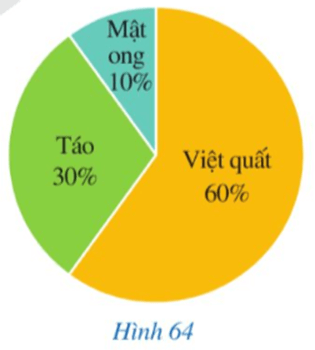
Lời giải:
Gọi các điểm A, B, C trên đường tròn (O) như hình vẽ.
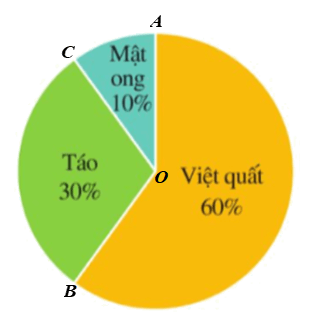
⦁ Do thành phần việt quất chiếm 60% thành phần nước ép hoa quả nên số đo cung nhỏ AB bằng 60% số đo của cung cả đường tròn. Vì thế,
⦁ Do thành phần táo chiếm 30% thành phần nước ép hoa quả nên số đo cung nhỏ BC bằng 30% số đo của cung cả đường tròn. Vì thế,
⦁ Do thành phần mật ong chiếm 10% thành phần nước ép hoa quả nên số đo cung nhỏ AC bằng 10% số đo của cung cả đường tròn. Vì thế,
Bài 5 trang 117 Toán 9 Tập 1:Cho hai đường tròn (O), (I) cắt nhau tại hai điểm A, B. Kẻ các đoạn thẳng AC, AD lần lượt là các đường kính của hai đường tròn (O), (I). Chứng minh ba điểm B, C, D thẳng hàng.
Lời giải:
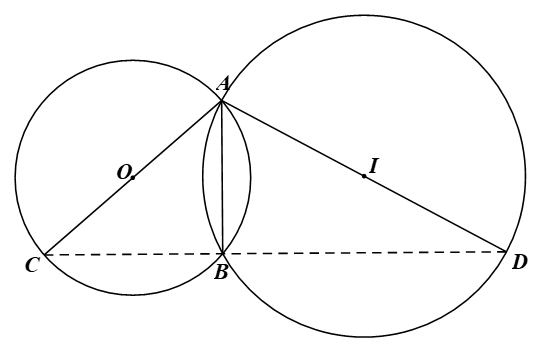
Ta có:
⦁(góc nội tiếp chắn nửa đường tròn (O)).
⦁(góc nội tiếp chắn nửa đường tròn (I)).
Suy rahay
Do đó ba điểm B, C, D thẳng hàng.
Bài 6 trang 117 Toán 9 Tập 1:Hãy sử dụng compa và thước thẳng để vẽ tam giác ABC vuông tại A và giải thích cách làm.
Lời giải:
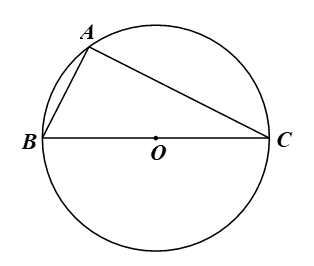
Bước 1.Vẽ đường tròn tâm O, kẻ đường kính BC.
Bước 2.Lấy điểm A thuộc đường tròn (O) (A khác B, C). Ta được tam giác ABC vuông tại A.
Thật vậy, xét đường tròn (O) có đường kính BC, điểm A thuộc (O) nên(góc nội tiếp chắn nửa đường tròn).
Vậy tam giác ABC vuông tại A.
Xem thêm các bài giải bài tập Toán lớp 9 Cánh diềuhay, chi tiết khác:
§3. Tiếp tuyến của đường tròn
§4. Góc ở tâm. Góc nội tiếp
§5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
Bài tập cuối chương 5
§1. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
§2. Tần số. Tần số tương đối
=============
THUỘC: Giải bài tập Toán 9 – SGK CÁNH DIỀU
