Giải SGK Toán 9 Bài 2 (Sách Cánh diều): Một số hệ thức về cạnh và góc trong tam giác vuông

Giải chi tiết Giải SGK Toán 9 Bài 2 (Sách Cánh diều): Một số hệ thức về cạnh và góc trong tam giác vuông – SÁCH GIÁO KHOA TOÁN 9 CÁNH DIỀU – 2024

================

Giải bài tập Toán 9 Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

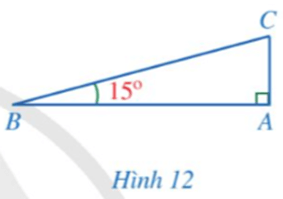
Khởi động trang 82 Toán 9 Tập 1:Hình 12mô tả đường lên dốc ởHình 11, trong đó góc giữa BC và phương nằm giữa BA là$\widehat{ABC}=15°.$

Cạnh góc vuông AC và cạnh huyền BC (Hình 12) có liên hệ với nhau như thế nào?

Lời giải:

Xét ∆ABC vuông tại A, ta có: sinB =$\frac{AC}{BC}$do đó AC = BC.sinB = BC.sin15°.

Hoạt động 1 trang 82 Toán 9 Tập 1:Cho tam giác ABC vuông tại A (Hình 13).

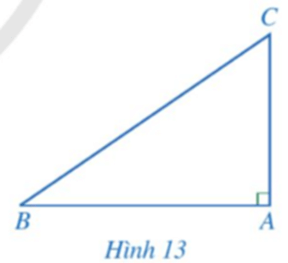
a) Biểu diễn sinB, cosC theo AC, BC.

b) Viết công thức tính AC theo BC và sinB.

c) Viết công thức tính AC theo BC và cosC.

Lời giải:

a) Xét ∆ABC vuông tại A, ta có: sinB =$\frac{AC}{BC}$và cosB =$\frac{AB}{BC}$.

b) Từ sinB =$\frac{AC}{BC}$(câu a) ta có AC = BC.sinB.

c) Từ cosB =$\frac{AB}{BC}$(câu a) ta có AC = BC.cosB.

Luyện tập 1 trang 83 Toán 9 Tập 1:Tính độ cao AC trongHình 12khi BC = 20 m (làm tròn kết quả đến hàng phần mười của mét).

Lời giải:

Xét ∆ABC vuông tại A, ta có: AC = BC.sinB = 20.sin15° ≈ 5,2 (m).

Luyện tập 2 trang 83 Toán 9 Tập 1:Cho tam giác nhọn ABC có đường cao CK. Biểu diễn CK theo AC và sinA. Từ đó, chứng minh diện tích của tam giác ABC bằng$\frac{1}{2}$.AB.AC.sinA.

Lời giải:

Xét ∆ACK vuông tại K, ta có: sinA =$\frac{CK}{AC}$do đó CK = AC.sinA.

Khi đó, diện tích của tam giác ABC là

$\frac{1}{2}$CK.AB =$\frac{1}{2}$.AC.sinA.AB=$\frac{1}{2}$.AB.AC.sinA.

Hoạt động 2 trang 84 Toán 9 Tập 1:Cho tam giác ABC vuông tại A (Hình 17).

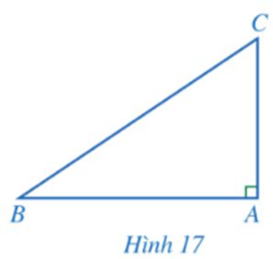
a) Biểu diễn tanB, cotC theo AB, AC.

b) Viết công thức tính AC theo AB và tanB.

c) Viết công thức tính AC theo AB và cotC.

Lời giải:

a) Xét ∆ABC vuông tại A, ta có: tanB =$\frac{AC}{AB}$và cotC =$\frac{AC}{AB}$.

b) Từ tanB =$\frac{AC}{AB}$(câu a) ta có AC = AB.tanB.

c) Từ cotC =$\frac{AC}{AB}$(câu a) ta có AC = AB.cotC.

Luyện tập 3 trang 84 Toán 9 Tập 1:Tính độ dài cạnh AB trongHình 17khi AC = 4 cm và$\hat{B}=34°$(làm tròn kết quả đến hàng phần mười của centimét).

Lời giải:

Xét ∆ABC vuông tại A, ta có AB = AC.cotB = 4.cot34° ≈ 5,9 (m).

Luyện tập 4 trang 85 Toán 9 Tập 1:Tìm độ dài cạnh góc vuông AC và số đo các góc nhọn B, C của tam giác vuông ABC, biết cạnh góc vuông AB = 5 cm và cạnh huyền BC = 13 cm.

Lời giải:

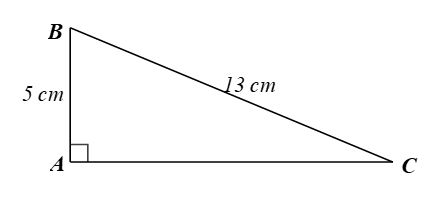
Xét ∆ABC vuông tại A, ta có:

⦁ BC²= AB²+ AC²(theo định lí Pythagore)

Suy ra AC²= BC²– AB²= 13²– 5²= 144.

Do đó AC = 12 (cm) (do AC > 0).

⦁ sinB =$\frac{AC}{BC}=\frac{12}{13}$suy ra$\hat{B}\approx 67°.$

⦁$\hat{B}+\hat{C}=90°$(tổng hai góc nhọn của tam giác vuông bằng 90°)

Suy ra$\hat{C}=90°-\hat{B}\approx 90°-67°=23°.$

Luyện tập 5 trang 85 Toán 9 Tập 1:Tìm số đo góc nhọn C và độ dài cạnh góc vuông AB, cạnh huyền BC của tam giác vuông ABC, biết cạnh góc vuông AC = 7 cm và$\hat{B}=55°.$

Lời giải:

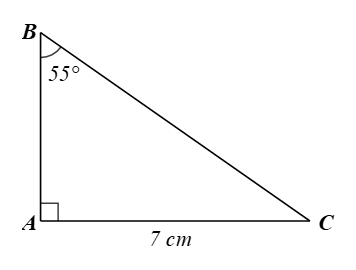
Xét ∆ABC vuông tại A, ta có:

⦁$\hat{B}+\hat{C}=90°$(tổng hai góc nhọn của tam giác vuông bằng 90°)

Suy ra$\hat{C}=90°-\hat{B}=90°-55°=35°.$

⦁ AB = AC.tanC = 7.tan35° ≈ 4,9 (cm).

⦁ AC = BC.sinB, suy ra$BC=\frac{AC}{\sin B}=\frac{7}{\sin 55°}\approx 8,5\text{(cm).}$

Luyện tập 6 trang 86 Toán 9 Tập 1:Cho hình chữ nhật ABCD thoả mãn AC = 6 cm,$\widehat{BAC}=47°.$Tính độ dài các đoạn thẳng AB, AD.

Lời giải:

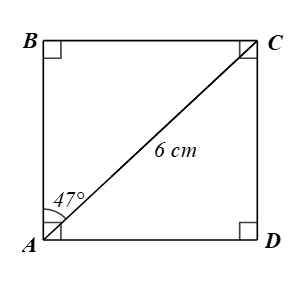
Xét ∆ABC vuông tại B, ta có:

⦁ AB = AC.cos$\widehat{BAC}$= 6.cos47^o$\approx$4.1 (cm).

⦁ BC = AC.sin$\widehat{BAC}$= 6.sin47^o$\approx$4,4 (cm).

Vì ABCD là hình chữ nhật nên AD = BC ≈ 4,4 cm (tính chất hình chữ nhật).

Bài tập

Bài 1 trang 86 Toán 9 Tập 1:Tìm x, y trong mỗi hình 23a, 23b, 23c (làm tròn kết quả đến hàng phần mười của centimét).

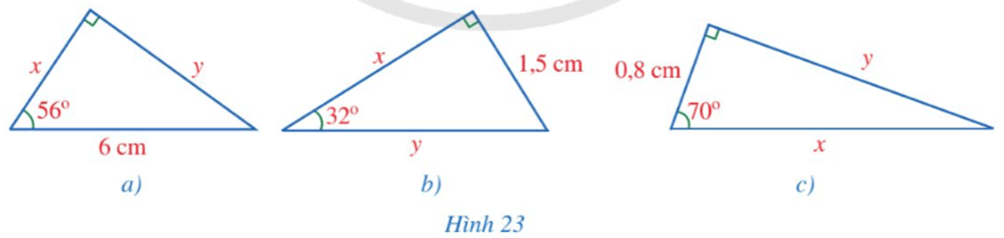
Lời giải:

a) Từ hình ta có:

⦁ x = 6.cos56° ≈ 3,4 (cm).

⦁ y = 6.sin56° ≈ 5,0 (cm).

b) Từ hình ta có:

⦁ x = 1,5.cot32° ≈ 2,4 (cm).

⦁ 1,5 = y.sin32°, suy ra$y=\frac{1,5}{\sin 32°}\approx 2,8$(cm).

c) Từ hình ta có:

⦁ 0,8 = x.cos70°, suy ra$x=\frac{0,8}{\cos 70°}\approx 2,3$(cm).

⦁ y = 0,8.tan70° ≈ 2,2 (cm).

Bài 2 trang 86 Toán 9 Tập 1:Cho tam giác ABC có đường cao AH = 6 cm,$\hat{B}=40°,\hat{C}=35°.$Tính độ dài các đoạn thẳng AB, BH, AC, BC (làm tròn kết quả đến hàng phần mười của centimét).

Lời giải:

Xét ∆ABH vuông tại H, ta có:

⦁ sinB =$\frac{AH}{AB}$, suy ra AB =$\frac{AH}{\sin {40}^o}$=$\frac{6}{\sin 40°}\approx$9,3 (cm).

⦁ BH = AH.cotB = 6.cot40° ≈ 7,2 (cm).

Xét ∆ACH vuông tại H, ta có:

⦁ sinC =$\frac{AH}{AC}$suy ra AC =$\frac{AH}{\sin 35°}=\frac{6}{\sin 35°}\approx$10,5 (cm).

⦁ CH = AH.cotC = 6.cot35° ≈ 8,6 (cm).

Khi đó, BC = BH + HC ≈ 7,2 + 8,6 = 15,8 (cm).

Bài 3 trang 86 Toán 9 Tập 1:Cho tam giác ABC vuông tại A có$\hat{B}=30°.$Chứng minh AC =$\frac{1}{2}$BC.

Lời giải:

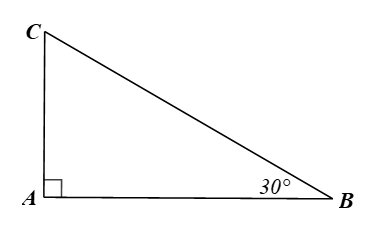
Xét ∆ABC vuông tại A, ta có: AC = BC.sinB = BC.sin30^o=$\frac{1}{2}$BC.

Vậy AC =$\frac{1}{2}$BC.

Bài 4 trang 87 Toán 9 Tập 1:Cho tam giác ABC vuông cân tại A. Chứng minh AB = AC =$\frac{\sqrt{2}}{2}$BC.

Lời giải:

Vì ∆ABC vuông cân tại A nên$\hat{B}=\hat{C}=45°$và AB = AC.

Ta có AB = BC.sinC = BC.$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$BC.

Mà AB = AC nên AB = AC =$\frac{\sqrt{2}}{2}$BC.

Bài 5 trang 87 Toán 9 Tập 1:TrongHình 24, cho$\hat{O}=\alpha$, AB = m và$\widehat{OAB}=\widehat{OCA}=\widehat{ODC}=90°.$

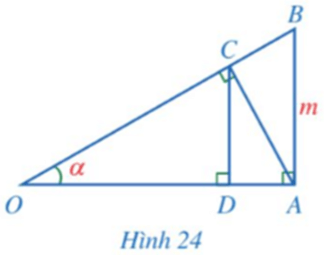
Chứng minh:

a) OA = m.cotα;

b) AC = m.cosα;

c) CD = m.cos²α.

Lời giải:

a) Xét ∆OAB vuông tại A, ta có: OA = AB.cotO = m.cotα.

b) Xét ∆OAC vuông tại C, ta có:

AC = OA.sinO = m.cot$\alpha$.sin$\alpha$= m.$\frac{\cos \alpha }{\sin \alpha }$.sin$\alpha$= mcos$\alpha$.

(Theo kết quả câu b, Bài 7, SGK Toán 9, Tập 1, trang 81 ta có cot$\alpha$=$\frac{\cos \alpha }{\sin \alpha }$).

c) Xét ∆OAC vuông tại C, ta có:

OC = OA.cosO = m.cot$\alpha$.cos$\alpha$= m.$\frac{\cos \alpha }{\sin \alpha }$.cos$\alpha$= m.$\frac{co{s}^2\alpha }{\sin \alpha }$.

(Theo kết quả câu b, Bài 7, SGK Toán 9, Tập 1, trang 81 ta có cot$\alpha$=$\frac{\cos \alpha }{\sin \alpha }$)

Xét ∆OCD vuông tại D, ta có:

CD = OC.sinO = m.$\frac{co{s}^2\alpha }{\sin \alpha }$.sin$\alpha$= mcos²$\alpha$.

Bài 6 trang 87 Toán 9 Tập 1:Tính độ dài đường gấp khúc ABCDEGH (làm tròn kết quả đến hàng phần mười của centimét), biết các tam giác OAB, OBC, OCD, ODE, OEG, OGH là các tam giác vuông tại các đỉnh lần lượt là B, C, D, E, G, H; các góc O₁, O₂, O₃, O₄, O₅, O₆đều bằng 30° và OA = 2 cm (Hình 25).

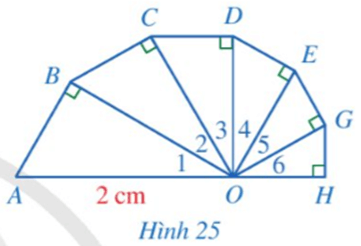
Lời giải:

Xét ∆OAB vuông tại B, có${\hat{O}}_1=30°,$theo Bài 3, SGK Toám 9, Tập 1, trang 86, ta có: AB =$\frac{1}{2}$AO =$\frac{1}{2}$.2 = 1 (cm).

Ta cũng có BO = AO.cos${\hat{O}}_1$= 2.cos30^o= 2.$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(cm).

Tương tự, ta cũng có:

⦁ BC =$\frac{1}{2}$BO =$\frac{1}{2}$.$\sqrt{3}$=$\frac{\sqrt{3}}{2}$(cm) và CO = BO.cos$\widehat{O_2}$=$\sqrt{3}$.$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$(cm).

⦁ CD =$\frac{1}{2}$CO =$\frac{1}{2}$.$\frac{3}{2}$=$\frac{3}{4}$(cm) và DO = CO.cos$\widehat{O_3}$=$\frac{3}{2}$.$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$(cm).

⦁ DE =$\frac{1}{2}$DO =$\frac{1}{2}$.$\frac{3\sqrt{3}}{4}$=$\frac{3\sqrt{3}}{8}$(cm) và EO = DO.cos$\widehat{O_4}$=$\frac{3\sqrt{3}}{4}$.$\frac{\sqrt{3}}{2}$=$\frac{9}{8}$(cm).

⦁ EG =$\frac{1}{2}$EO =$\frac{1}{2}$.$\frac{9}{8}$=$\frac{9}{16}$(cm) và GO = EO.cos$\widehat{O_5}$=$\frac{9}{8}$.$\frac{\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{16}$(cm).

⦁ GH =$\frac{1}{2}$GO =$\frac{1}{2}$.$\frac{9\sqrt{3}}{16}$=$\frac{9\sqrt{3}}{32}$(cm).

Vậy độ dài đường gấp khúc ABCDEGH là:

$1+\frac{\sqrt{3}}{2}+\frac{3}{4}+\frac{3\sqrt{3}}{8}+\frac{9}{16}+\frac{9\sqrt{3}}{32}$

$=\frac{32}{32}+\frac{16\sqrt{3}}{32}+\frac{24}{32}+\frac{12\sqrt{3}}{32}+\frac{18}{32}+\frac{9\sqrt{3}}{32}=\frac{74+37\sqrt{3}}{32}\approx \text{4,3 (cm).}$

Bài 7 trang 87 Toán 9 Tập 1:Hình 26minh hoạ một phần con sông có bề rộng AB = 100 m. Một chiếc thuyền đi thẳng từ vị trí B bên này bờ sông đến vị trí C bên kia bờ sông. Tính quãng đường BC (làm tròn kết quả đến hàng phần mười của mét), biết$\widehat{ABC}=35°.$

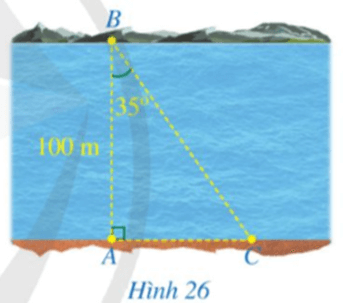
Lời giải:

Xét ∆ABC vuông tại A, ta có:

cos B =$\frac{AB}{BC}$, suy ra BC =$\frac{AB}{\cos B}$=$\frac{100}{\cos {35}^o}$$\approx$122,1 (m).

Bài 8 trang 87 Toán 9 Tập 1:Từ vị trí A ở phía trên một tòa nhà có chiều cao AD = 68 m, bác Duy nhìn thấy vị trí C cao nhất của một tháp truyền hình, góc tạo bởi tia AC và tia AH theo phương nằm ngang là$\widehat{CAH}=43°.$Bác Duy cũng nhìn thấy chân tháp tại vị trí B mà góc tạo bởi tia AB và tia AH là$\widehat{BAH}=28°,$điểm H thuộc đoạn thẳng BC (Hình 27). Tính khoảng cách BD từ chân tháp đến chân tòa nhà và chiều cao BC của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).

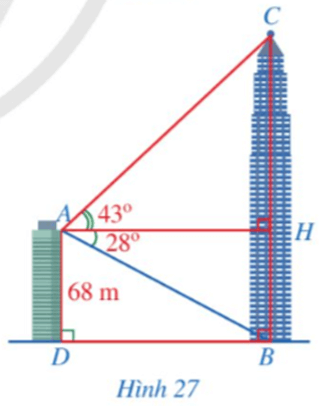
Lời giải:

Vì AH ⊥ BC và BD ⊥ BC nên AH // BD. Do đó$\widehat{ABD}=\widehat{BAH}=28°$(so le trong).

Khoảng cách BD từ chân tháp đến chân tòa nhà là:

BD = AD.cot$\widehat{ABD}$= 68.cot28^o$\approx$127,9 (m).

Do tứ giác ADBH có$\widehat{ADB}=\widehat{AHB}=\widehat{DBH}=90°$nên ADBH là hình chữ nhật.

Suy ra AH = DB ≈ 127, 9 (m) và HB = AD = 68 (m).

Do ∆AHC vuông tại H, ta có CH = AH.tan$\widehat{CAH}$$\approx$127,9.tan43^o$\approx$119,3 (m).

Chiều cao BC của tháp truyền hình là:

BC = BH + HC ≈ 68 + 119,3 = 187,3 (m).

Vậy khoảng cách BD từ chân tháp đến chân tòa nhà khoảng 127,9 mét và chiều cao BC của tháp truyền hình khoảng 187,3 mét.

Xem thêm các bài giải bài tập Toán lớp 9 Cánh diềuhay, chi tiết khác:

§1. Tỉ số lượng giác của góc nhọn

§2. Một số hệ thức về cạnh và góc trong tam giác vuông

§3. Ứng dụng của tỉ số lượng giác của góc nhọn

Bài tập cuối chương 4

§1. Đường tròn. Vị trí tương đối của hai đường tròn

§2. Vị trí tương đối của đường thẳng và đường tròn

=============
THUỘC: Giải bài tập Toán 9 – SGK CÁNH DIỀU