Giải SGK Toán 12 (Sách KNTT): Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình

Giải chi tiết Giải SGK Toán 12 (Sách KNTT): Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình – SÁCH GIÁO KHOA TOÁN 12 KẾT NỐI – 2024

================

Giải bài tập Toán 12 Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình

Thực hành 1 trang 82 Toán 12 Tập 2: Sử dụng phần mềm Geogebra, tính:

a) $\int \frac{x^2-2x+2}{x+1}dx$

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{e}^x\cos 2xdx$

Lời giải:

Khởi động phần mềm Geogebra, chọn Complex Adaptive System (CAS) để thực hiện tính toán nguyên hàm và tích phân.

a) Để tính $\int \frac{x^2-2x+2}{x+1}dx$, ta dùng lệnh IntegralSymbolic($\frac{x^2-2x+2}{x+1}$), kết quả sẽ được hiển thị ngay bên dưới như hình sau:

Vậy $\int \frac{x^2-2x+2}{x+1}dx$ = 5ln|x + 1| + $\frac{1}{2}$x² – 3x + C.

b) Để tính gần đúng tích phân $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{e}^x\cos 2xdx$, ta dùng lệnh Nintegral(e^xcos2x, 0, $\frac{\pi }{2}$), kết quả sẽ được hiển thị ngay bên dưới như hình sau:

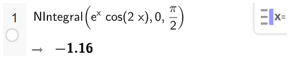
Vậy $\underset{0}{\overset{\frac{\pi }{2}}{\int }}{e}^x\cos 2xdx$ ≈ – 1,16.

Thực hành 2 trang 84 Toán 12 Tập 2: Sử dụng phương pháp hình thang, tính gần đúng $\underset{1}{\overset{2}{\int }}\frac{e^x}{x}dx$ với độ chính xác 0,01.

Lời giải:

1. Ta có: $f\left(x\right)=\frac{e^x}{x}$

$f^{‘}\left(x\right)={\left(\frac{e^x}{x}\right)}^{‘}=\frac{e^x\cdot x-e^x}{x^2}=\left(\frac{1}{x}-\frac{1}{x^2 }\right)e^x;$

$f^{”}\left(x\right)={\left[\left(\frac{1}{x}-\frac{1}{x^2 }\right)e^x\right]}^{‘}=\left(\frac{1}{x}-\frac{2}{x^2}+\frac{2}{x^3}\right)e^x$

${}^{}{}^{}{f}^{‘}‘‘\left(x\right)={\left[\left(\frac{1}{x}-\frac{2}{x^2}+\frac{2}{x^3}\right)e^x\right]}^{‘}=\left(\frac{1}{x}-\frac{3}{x^2}+\frac{6}{x^3}-\frac{6}{x^4}\right)e^x$

f”'(x) = 0 thì x ≈ 1,596.

Ta có f”(1) = e; f”(1,596) ≈ 0,333 ∙ e^1,569; f”(2) = $\frac{e^2}{4}$

Do đó, $M=\underset{x\in \left[1;2\right]}{\max }\left|f^{”}\left(x\right)\right|=e$

2. Ta cần tìm n sao cho:

$\frac{{\left(2-1\right)}^3\cdot e}{12n^2}<\mathrm{0,01}\iff \frac{e}{12n^2}<\mathrm{0,01}\iff n>\sqrt{\frac{25e}{3}}$.

Do đó, ta chọn n = 5.

3. Chia đoạn [1; 2] thành 5 đoạn có độ dài bằng nhau là [1; 1,2], [1,2; 1,4], [1,4; 1,6], [1,6; 1,8], [1,8; 2].

Áp dụng công thức hình thang, ta có:

$\underset{1}{\overset{2}{\int }}\frac{e^x}{x}dx$$\approx \frac{2-1}{2\cdot 5}\left[\frac{e^1}{1}+2\cdot \frac{e^{\mathrm{1,2}}}{\mathrm{1,2}}+2\cdot \frac{e^{\mathrm{1,4}}}{\mathrm{1,4}}+2\cdot \frac{e^{\mathrm{1,6}}}{\mathrm{1,6}}+2\cdot \frac{e^{\mathrm{1,8}}}{\mathrm{1,8}}+\frac{e^2}{2}\right]$≈ 3,065.

Vận dụng trang 84 Toán 12 Tập 2: Một thân cây dài 4,8 m được cắt thành các khúc gỗ dài 60 cm. Người ta đo đường kính của mỗi mặt cắt ngang và diện tích S của nó được ghi lại trong bảng dưới đây, ở đây x (cm) là khoảng cách tính từ đỉnh thân cây đến vết cắt.

x (cm)	0	60	120	180	240	300	360	420	480
S (cm2)	240	248	256	260	264	272	298	316	320

Tìm thể tích gần đúng của thân cây này.

Hướng dẫn.

Thể tích cần tính là $V=\underset{0}{\overset{480}{\int }}S\left(x\right)dx$, trong đó S(x) là diện tích mặt cắt ngang tại vị trí cách đỉnh thân cây một khoảng x (cm). Sử dụng phương pháp hình thang để tính gần đúng tích phân này.

Lời giải:

Thể tích gần đúng của thân cây đã cho là $V=\underset{0}{\overset{480}{\int }}S\left(x\right)dx$

Ta chia đoạn [0; 480] thành n = 8 đoạn con có độ dài bằng nhau, mỗi đoạn có độ dài là 60. Các đoạn đó là: [0; 60], [60; 120], [120; 180], [180; 240], [240; 300], [300; 360], [360; 420], [420; 480].

Áp dụng công thức hình thang, ta có:

$V=\underset{0}{\overset{480}{\int }}S\left(x\right)dx$$\approx \frac{480-0}{2\cdot 8}$ (240 + 2 ∙ 248 + 2 ∙ 256 + 2 ∙ 260 + 2 ∙ 264 + 2 ∙ 272 + 2 ∙ 298 + 2.316 + 320] = 131 640 (cm³) = 0,13164 (m³_­).

=============
THUỘC: Giải bài tập Toán 12 – SGK KẾT NỐI