Giải SBT Đề kiểm tra Chương 3 – Hình học 10

Đề 1

Câu 1.  (8 điểm)   

Trong mặt phẳng Oxy, cho tam giác ABC có ba đỉnh A(1;-1), B(2;-3), C(3;3).

a) Tìm số đo của góc A của tam giá ABC;

b) Viết phương trình các cạnh AB, AC ;

c) Viết phương trình đường phân giác trong góc A của tam giác ABC.

Bài giải

a) \(\cos A =  – {3 \over 5} \Rightarrow \widehat A \approx {126^ \circ }{52′}.\)

b) \(AB:2x + y – 1 = 0,\,AC:2x – y – 3 = 0.\)

c) Phân giác trong AD có phương trình : y + 1 = 0

Câu 2.  (2 điểm)    

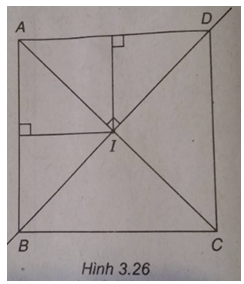
Trong mặt phẳng Oxy, cho hình vuông ABCD có tâm I(2;0), cạnh AB: 2x + y + 1 = 0 và A có hoành độ âm.

a) Lập phương trình cạnh AD của hình vuông ;

b) Lập phương trình đường chéo BD của hình vuông.

HD giải

a) \(AD \bot AB \Rightarrow \) phương trình AD có dạng x – 2y + c = 0.

\(d(I,AD) = d(I,AB)\)

\( \Leftrightarrow {{\left| {2 + c} \right|} \over {\sqrt 5 }} = {{\left| {4 + 1} \right|} \over {\sqrt 5 }}\)

\( \Leftrightarrow \left[ \matrix{
c = 3 \hfill \cr
c = – 7\,\,\,(*)\, \hfill \cr} \right.\)

(*) loại do A có hoành độ âm

Vậy phương trình AD là : x – 2y + 3 = 0.

b) A(-1 ; 1), BD vuông góc với AI tại I,

BD có phương trình là : 3x – y – 6 = 0.

---

Đề 2

Câu 1.  (6 điểm)

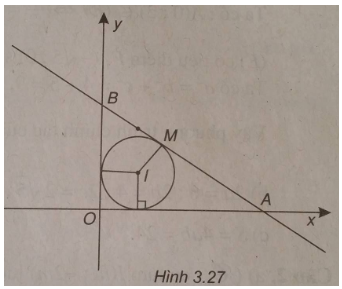
Trong mặt phẳng tọa độ Oxy, cho điểm \(M\left( {2;{3 \over 2}} \right)\)

a) Viết phương trình đường tròn  (C)  có đường kính OM ;

b) Viết phương trình đường thẳng d đi qua M và cắt hai nửa trục dương Ox, Oy lần lượt tại A, B sao cho diện tích tam giác OAB bằng 6 đơn vị diện tích ;

c) Tìm tọa độ tâm I của đường tròn nội tiếp (T) của tam giác OAB. Viết phương trình đường tròn đó.

a) Đường trìn đường kính OM có tâm \(J\left( {1;{3 \over 4}} \right)\) là trung điểm của đoạn OM và có bán kính \(R = {{OM} \over 2} = {5 \over 4}\).

Phương trình của  (C)  là :

\({\left( {x – 1} \right)^2} + {\left( {y – {3 \over 4}} \right)^2} = {{25} \over {16}}.\)

b) Đặt A(a;0), B(0;b) với a>0, b>0, ta có:

\(\left\{ \matrix{
{2 \over a} + {{{3 \over 2}} \over b} = 1 \hfill \cr
ab = 12 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 4 \hfill \cr
b = 3. \hfill \cr} \right.\)

Vậy phương trình AB là :

3x + 4y – 12 = 0.

c) Đặt I(c;c) là tâm đường tròn nội tiếp tam giác OAB, ta có: d(I;AB) = c

\( \Leftrightarrow {{\left| {3c + 4c – 12} \right|} \over 5} = c\left( {0 < c < {3 \over 2}} \right)\)

\(\eqalign{
& \Leftrightarrow {\left( {7c – 12} \right)^2} = 25{c^2} \cr
& \Leftrightarrow 24{c^2} – 168c + 144 = 0 \cr} \)

\( \Leftrightarrow \left[ \matrix{
c = 1 \hfill \cr
c – 6\,(*) \hfill \cr} \right.\)

( (*) loại)

Vậy phương trình đường tròn nội tiếp tam giác OAB là : \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} = 1.\)

Câu 2  (4 điểm)    

Trong mặt phẳng Oxy, cho điểm A(8;-1), và đường tròn  (C)  : \({x^2} + {y^2} – 6x – 4y + 4 = 0\)

a) Viết phương trình các tiếp tuyến vơi  (C)  vẽ từ A ;

b) Gọi M và N là các tiếp điểm của các tiếp tuyến trên vơi  (C) . Tính độ dài đoạn MN.

Gợi ý làm bài

a) y + 1 = 0 hay 15x + 8y – 112 = 0.

b) \(MN = {{30} \over {\sqrt {34} }}\)

---

Đề 3

Câu 1.  (8 điểm)   

a) Viết phương trình chính tắc của elip (E) đi qua điểm A(0;2) và có một tiêu điểm là \({F_1}\left( { – \sqrt 5 ;0} \right)\)

b) Tìm độ dài trục lớn, trục nhỏ, tiêu cự và tỉ số \({c \over a}\) của elip (E) ;

c) Tìm diện tích của hình chữ nhật cơ sở của (E).

Bài giải

a) Phương trình chính tắc của (E) có dạng:

\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\) với 0<b<a

Ta có : \(A(0;2) \in (E) \Leftrightarrow {4 \over {{b^2}}} = 1 \Leftrightarrow b = 2.\)

(E) có tiểu điểm \({F_1}\left( { – \sqrt 5 ;0} \right)\) suy ra \(c = \sqrt 5 .\)

Ta có \({a^2} = {b^2} + {c^2} = 4 + 5 = 9\), suy ra  a = 3.

Vậy phương trình chính tắc của elip (E) là: \({{{x^2}} \over 9} + {{{y^2}} \over 4} = 1.\)

b) \(\eqalign{
& 2a = 6\,;\,2b = 4\,; \cr
& \,2c = 2\sqrt 5 \,;\,{c \over a} = {{\sqrt 5 } \over 3}. \cr} \)

c) S = 4ab = 24.

Câu 2  (2 điểm)    

Cho đường tròn  (C m)  : \({x^2} + {y^2} – 2mx + 4my + 5{m^2} – 1 = 0\)

a) Chứng minh rằng họ  (C m)   luôn luôn tiếp xúc với hai đường thẳng cố định ;

b) Tìm m để  (C m)  cắt đường tròn  (C ) : \({x^2} + {y^2} = 1\) tại hai điểm phân biệt A và B.

Giải

a)  (C m)  có tâm I(m;-2m) luôn thuộc đường thẳng d: 2x + y = 0 và có bán kính không  đổi R = 1.

Vậy  (C m)  luôn tiếp xúc với hai đường thẳng cố định, đó là hai tiếp tuyến của  (C m)  song song với d.

b) \(0 < \left| m \right| < {2 \over {\sqrt 5 }}\)

—— HẾT ——–