Giải SBT Câu hỏi và bài tập Ôn tập Chương 2 – Hình học 10

Bài 2.45 trang 103

Cho tam giác ABC thỏa mãn điều kiện \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB}  – \overrightarrow {AC} } \right|\). Vậy tam giác ABC là tam giác gì?

HD giải

Gọi M là trung điểm của cạnh BC ta có:

\(\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM}  = \overrightarrow {AD} \)

Mặt khác \(\overrightarrow {AB}  – \overrightarrow {AC}  = 2\overrightarrow {CB} \). Theo giả thiết ta có:

\(\left| {2\overrightarrow {AM} } \right| = \left| {\overrightarrow {CB} } \right| = \left| {\overrightarrow {AD} } \right|\)

Hay \(AM = {{BC} \over 2}\)

Ta suy ra ABC là tam giác vuông tại A.

Bài 2.46 trang 103

Ba điểm A, B, C phân biệt tạo nên vec tơ \(\overrightarrow {AB}  + \overrightarrow {AC} \) vuông góc với vec tơ  \(\overrightarrow {AB}  + \overrightarrow {CA} \). Vậy tam giác ABC là tam giác gì?

Gợi ý làm bài

Theo giả thiết ta có:

\(\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right).\left( {\overrightarrow {AB}  + \overrightarrow {CA} } \right) = 0\)

\(\eqalign{
& \Leftrightarrow \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {AB} – \overrightarrow {AC} } \right) = 0 \cr
& \Leftrightarrow {\overrightarrow {AB} ^2} – \overrightarrow {AC} {}^2 = 0 \cr} \)

Ta suy ra ABC là tam giác có AB = AC (tam giác cân tại A)

Bài 2.47 – Ôn tập chương 2

Tính các cạnh còn lại của tam giác ABC trong mỗi trường hợp sau:

a) \(a = 7,b = 10,\widehat C = {56^0}29’\)

b) \(a = 2,c = 3,\widehat B = {123^0}17’\)

c) \(b = 0,4,c = 12,\widehat A = {23^0}28’\)

Giải

a) \(\eqalign{
& {c^2} = {a^2} + {b^2} – 2ab\cos C \cr
& = 49 + 100 – 140\cos {56^0}29′ \cr} \)

=> \({c^2} \approx 71,7\) hay \(c \approx 8,47\)

b) \(b \approx 4,43\)

c) \(a \approx 11,63\)

Bài 2.48 trang 104 SBT Hình học 10

Tam giác ABC có \(\widehat B = {60^0},\widehat C = {45^0},BC = a\). Tính độ dài hai cạnh AB và AC.

Lời giải

Ta có: \(\widehat A = {180^0} – ({60^0} + {45^0}) = {75^0}\)

Đặt AC = b, AB = a. Theo định lí sin:

\({b \over {\sin {{60}^0}}} = {a \over {\sin {{75}^0}}} = {c \over {\sin {{45}^0}}}\).

Ta suy ra

\(AC = b = {{a\sqrt 3 } \over {2\sin {{75}^0}}} \approx {{a\sqrt 3 } \over {1,93}} \approx 0,897a\)

\(AB = c = {{a\sqrt 2 } \over {2\sin {{75}^0}}} \approx {{a\sqrt 2 } \over {1,93}} \approx 0,732a\)

Bài 2.49 trang 104

Tam giác ABC có \(\widehat A = {60^0},\,\,b = 20,\,\,c = 35\)

a) Tính chiều cao \({h_a}\);

b) Tính bán kính đường tròn ngoại tiếp tam giác;

c) Tính bán kính đường tròn nội tiếp tam giác.

Ta có:

\(\eqalign{
& {a^2} = {b^2} + {c^2} – 2bc\cos A \cr
& = {20^2} + {35^2} – 20.35 = 925 \cr} \)

Vậy \(a \approx 30,41\)

a) Từ công thức \(S = {1 \over 2}a{h_a}\) ta có \({h_a} = {{2S} \over a} = {{bc\sin A} \over a}\)

\(=  > {h_a} \approx {{20.35.{{\sqrt 3 } \over 2}} \over {30,41}} \approx 19,93\)

b) Từ công thức \({a \over {\sin A}} = 2R\) ta có \(R = {a \over {\sqrt 3 }} \approx {{30,41} \over {\sqrt 3 }} \approx 17,56\)

c) Từ công thức \(S = pr\) với \(p = {1 \over 2}(a + b + c)\), ta có:

\(r = {{2S} \over {a + b + c}} = {{bc\sin A} \over {a + b + c}} \approx 7,10\)

Bài 2.50 trang 104 Ôn tập chương 2

Cho tam giác ABC có BC = a, CA = b, AB = c. Chứng minh rằng

\({b^2} – {c^2} = a(b\cos C – c\cos B)\)

Gợi ý làm bài

Ta có: \({b^2} = {a^2} + {c^2} – 2ac\cos B\)

\({c^2} = {a^2} + {b^2} – 2ab\cos C\)

\( =  > {b^2} – {c^2} = {c^2} – {b^2} + 2a(b\cos C – c\cos B)\)

\( =  > 2({b^2} – {c^2}) = 2a(b\cos C – c\cos B)\)

Hay \({b^2} – {c^2} = a(b\cos C – c\cos B)\)

Bài 2.51

Tam giác ABC có BC = 12, CA = 13, trung tuyến AM = 8

a) Tính diện tích tam giác ABC;

b) Tính góc B.

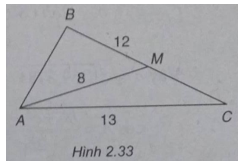
Theo công thức Hê – rông ta có:

\({S_{AMC}} = \sqrt {{{27} \over 2}\left( {{{27} \over 2} – 13} \right)\left( {{{27} \over 2} – 6} \right)\left( {{{27} \over 2} – 8} \right)} \)

\( = {{9\sqrt {55} } \over 4}\)

\({S_{ABC}} = 2{S_{AMC}} = {{9\sqrt {55} } \over 2}\)

Mặt khác ta có \(A{M^2} = {{{b^2} + {c^2}} \over 2} – {{{a^2}} \over 4}\) hay \(2A{M^2} = {b^2} + {c^2} – {{{a^2}} \over 2}\)

Do đó

\(\eqalign{
& A{B^2} = {c^2} = 2A{M^2} – {b^2} + {{{a^2}} \over 2} \cr
& = 2.64 – 169 + 72 = 31 \cr} \)

\( =  > c = \sqrt {31} \)

\(\eqalign{
& \cos B = {{{a^2} + {c^2} – {b^2}} \over {2ac}} = {{144 + 31 – 169} \over {24\sqrt {31} }} \cr
& \approx 0,045 = > \widehat B \approx {87^0}25′ \cr} \)

Bài 2.52

Giải tam giác ABC biết: a = 14, b = 18, c = 20

Bài giải

Tam giác ABC có cạnh là BC = 14, CA = 18, AB = 20, ta cần tìm các góc \(\widehat A,\widehat B,\widehat C\)

Ta có:

\(\eqalign{
& \cos A = {{{b^2} + {c^2} – {a^2}} \over {2bc}} \cr
& = {{{{18}^2} + {{20}^2} – {{14}^2}} \over {2.18.20}} \approx 0,7333 \cr} \)

\( =  > \widehat A \approx {42^0}50’\)

\(\eqalign{
& \cos B = {{{a^2} + {c^2} – {b^2}} \over {2ac}} \cr
& = {{{{14}^2} + {{20}^2} – {{18}^2}} \over {2.14.20}} \approx 0,4857 \cr
& = > \widehat B \approx {60^0}56′ \cr} \)

\(\widehat C = {180^0} – (\widehat A + \widehat B) \approx {76^0}14’\)

Bài 2.53 trang 104 SBT Toán 10

Giải tam giác ABC biết: \(\widehat A = {60^0},\widehat B = {40^0};c = 14\)

Bài giải

Tam giác ABC có cạnh c = AB = 14 và có \(\widehat A = {60^0},\widehat B = {40^0}\). Ta có: \(\widehat C = {180^0} – (\widehat A + \widehat B) = {80^0}\) cần tìm a và  b. Theo định lí sin:

\({a \over {\sin A}} = {b \over {\sin B}} = {c \over {\sin C}}\) ta suy ra \(a = {{c\sin A} \over {\sin C}} = {{7\sqrt 3 } \over {\sin {{80}^0}}} \approx 12,31\)

\(b = {{c\sin B} \over {\sin C}} = {{14\sin {{40}^0}} \over {\sin {{80}^0}}} \approx 9,14\)

Bài 2.54 trang 104 Ôn tập chương 2 hình 10

Cho tam giác ABC có \(a = 49,4,b = 26,4,\widehat C = {47^0}20’\). Tính \(\widehat A,\widehat B\) và cạnh C

Theo định lí cô sin ta có:

\(\eqalign{
& {c^2} = {a^2} + {b^2} – 2ab\cos C \cr
& = {(49,4)^2} + {(26,4)^2} – 2.49,4.26,4.\cos {47^0}20′ \cr
& \approx 1369,5781 \cr} \)

Vậy \(c = \sqrt {1369,5781}  \approx 37\)

\(\eqalign{
& \cos A = {{{b^2} + {c^2} – {a^2}} \over {2bc}} \cr
& \approx {{{{(26,4)}^2} + {{(37)}^2} – {{(49,4)}^2}} \over {2.26,4.37}} \approx – 0,1916 \cr} \)

Ta suy ra \(\widehat A \approx {101^0}3’\)

\(\widehat B \approx {180^0} – ({101^0}3′ + {47^0}20′) = {31^0}37’\)