Giải bài tập SBT Toán đại số 10: Bài tập ôn tập chương 4 – bài 59, 60, 61, 62, 63, 64 trang 124; bài 65, 66, 67 trang 125 Sách bài tập (SBT) Toán Đại số 10.
Bài 59 trang 124 SBT Toán Đại số 10
Chứng minh rằng:
\({({x^2} – {y^2})^2} \ge 4xy{(x – y)^2},\forall x,y.\)
Trả lời:
\({({x^2} – {y^2})^2} – 4xy{(x – y)^2} = {(x – y)^2}{\rm{[(x + y}}{{\rm{)}}^2}{\rm{ – 4xy]}}\)
\( = {(x – y)^2}{(x – y)^2} \ge 0 = > {({x^2} – {y^2})^2} \ge 4xy{(x – y)^2},\forall x,y\)
Bài 60 trang 124
Chứng minh rằng:
\({x^2} + 2{y^2} + 2xy + y + 1 > 0,\forall x,y.\)
Bài giải
\({x^2} + 2{y^2} + 2xy + y + 1 = {(x + y)^2} + {(y + {1 \over 2})^2} + {3 \over 4}\forall x,y\)
Bài 61 trang 124 – ôn tập chương 4 đại số 10
Chứng minh rằng:
\((a + 1)(b + 1)(a + c)(b + c) \ge 16abc\), với a, b, c là những số dương tùy ý.
Giải
\((a + 1)(b + 1)(a + c)(b + c) \ge 2\sqrt a .2\sqrt b .2\sqrt {ac} .2\sqrt {bc} \)
\(2\sqrt a .2\sqrt b .2\sqrt {ac} .2\sqrt {bc} = 16abc.\)
=> \((a + 1)(b + 1)(a + c)(b + c) \ge 16abc.\)
Bài 62 – Ôn tập chương 4 Đại số 10
Chứng minh rằng:
\(a + b + b \le {1 \over 2}({a^2}b + {b^2}c + {c^2}a + {1 \over a} + {1 \over b} + {1 \over c}).\)
Với a, b, c là những số dương tùy ý.
Hướng dẫn:
Theo bài 7 ta có:
\({a^2}b + {1 \over b} \ge 2a\), do đó
\(a \le {1 \over 2}({a^2}b + {1 \over b})\)
Tương tự: \(b \le {1 \over 2}({b^2}c + {1 \over c})\)
\(c \le {1 \over 2}({c^2}a + {1 \over a})\)
Cộng từng vế ba bất đẳng thức này ta được điều phải chứng minh.
Bài 63 trang 124 Sách bài tập Toán Đại số 10
Cho a, b, c là ba số thực thỏa mãn điều kiện \({a^3} > 36\) và abc = 1
Xét tam thức bậc hai \(f(x) = {x^2} – {\rm{a}}x – 3ac + {{{a^2}} \over 3}\)
a) Chứng minh rằng \(f(x) > 0,\forall x\);
b) Từ câu a) suy ra \({{{a^2}} \over 3} + {b^2} + {c^2} > ab + bc + ca.\)
Bài làm
a) f(x) có
\(\eqalign{
& \Delta = {a^2} – 4( – 3bc + {{{a^2}} \over 3}) = {{ – {a^2}} \over 3} + 12bc \cr
& = {{ – {a^2}} \over 3} + {{12abc} \over a} = {{ – {a^2}} \over 3} + {{12} \over a} \cr} \)
\( = {{36 – {a^3}} \over {3a}} < 0\) (do giả thiết \({a^3} > 36\))
=> \(f(x) > 0,\forall x\)
b) \({{{a^2}} \over 3} + {b^2} + {c^2} > ab + bc + ca\)
\( \Leftrightarrow {{{a^2}} \over 3} + {(b + c)^2} – 2bc > bc + a(b + c)\)
\( \Leftrightarrow {(b + c)^2} – a(b + c) – 3bc + {{{a^2}} \over 3} > 0\)
\( \Leftrightarrow f(b + c) > 0\) đúng vì \(f(x) > 0,\forall x.\)
Bài 64 trang 124
Giải và biện luận bất phương trình sau theo tham số m.
\((m – 1).\sqrt x \le 0\)
Hướng dẫn giải
Điều kiện của bất phương trình là \(x \ge 0\)
Nếu \(m \le 1\) \(m – 1 \le 0\) , bất phương trình đã cho nghiệm đúng với mọi \(x \ge 0\)
Nếu m > 1 thì m – 1 > 0, bất phương trình đã cho tương đương với
\(\sqrt x \le 0 \Leftrightarrow x = 0\)
Trả lời: Nếu \(m \le 1\) thì tập nghiệm của bất phương trình là \({\rm{[}}0; + \infty )\)
Nếu m > 1 thì tập nghiệm của bất phương trình là {0}
Bài 65 trang 125 SBT Đại số 10
Tìm a và b để bất phương trình
\((x – 2a + b – 1)(x + a – 2b + 1) \le 0\)
Có tập nghiệm là đoạn [0;2].
Lời giải
Tập nghiệm của bất phương trình đã cho là đoạn \({\rm{[}}2a – b + 1; – a + 2b – 1]\) (nếu \(2a – b + 1 \le – a + 2b – 1\)) hoặc là đoạn \({\rm{[}} – a + 2b – 1;2a – b + 1]\) (nếu \( – a + 2b – 1 \le 2a – b – 1\))
Do đó để tập nghiệm của bất phương trình đã cho là đoạn [0;2], điều kiện cần và đủ là:
\((1)\,\left\{ \matrix{
2a – b + 1 = 2 \hfill \cr
– a + 2b – 1 = 0 \hfill \cr} \right.\)
hoặc
\((2)\,\left\{ \matrix{
2a – b + 1 = 0 \hfill \cr
– a + 2b – 1 = 2. \hfill \cr} \right.\)
Giải (1) ta được a = b = 1. Giải hệ (2) ta được \(a = {1 \over 3},b = {5 \over 3}\)
Đáp số: a = b = 1 hoặc \(a = {1 \over 3},b = {5 \over 3}\)
Bài 66 trang 125
Tìm a và b (b > -1) để hai bất phương trình sau tương đương
\((x – a + b)(x + 2a – b – 1) \le 0\) (1)
Và \(\left| {x + a – 2} \right| \le b + 1.\) (2)
Gợi ý làm bài
(1) \( \Leftrightarrow x \in {\rm{[}}\alpha ;\beta {\rm{]}}\), trong đó
\(\left\{ \matrix{
\alpha = a – b \hfill \cr
\beta = – 2a + b + 1 \hfill \cr} \right.\)
hoặc
\(\left\{ \matrix{
\alpha = – 2a + b + 1 \hfill \cr
\beta = a – b. \hfill \cr} \right.\)
(2) \( \Leftrightarrow – (b + 1) \le x + a – 2 \le b + 1\)
\(\Leftrightarrow – b – a + 1 \le x \le – a + b + 3\)
\(\Leftrightarrow x \in {\rm{[}} – b – a + 1; – a + b + 3]\)
(1) và (2) tương đương khi và chỉ khi \({\rm{[}}\alpha ;\beta {\rm{]}} = {\rm{[}} – b – a + 1; – a + b + 3]\), tức là:
\(\left\{ \matrix{
\alpha = – b – a + 1 \hfill \cr
\beta = – a + b + 3 \hfill \cr} \right.\)
\( \Leftrightarrow (3)\left\{ \matrix{
a – b = – b – a + 1 \hfill \cr
– 2a + b + 1 = – a + b + 3 \hfill \cr} \right.\)
hoặc
\(\left\{ \matrix{
– 2a + b + 1 = – b – a + 1 \hfill \cr
a – b = – a + b + 3 \hfill \cr} \right.\)
Hệ phương trình (3) vô nghiệm. Hệ phương trình (4) có nghiệm duy nhất \(a = 3,b = {3 \over 2}\)
Đáp số: \(a = 3,b = {3 \over 2}\).
Bài 67 trang 125
a) Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau
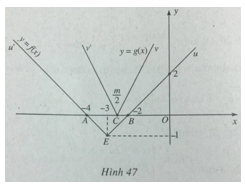
\(y = f(x) = \left| {x + 3} \right| – 1\);
\(y = g(x) = \left| {2x – m} \right|\); trong đó m là tham số
Xác định hoành độ các giao điểm của mỗi đồ thị với trục hoành.
b) Tìm các giá trị của tham số m để bất phương trình sau nghiệm đúng với mọi giá trị của x
\(\left| {2x – m} \right| > \left| {x + 3} \right| – 1\)
Gợi ý làm bài
a) Đồ thị hàm số y = f(x) là đường gấp khúcu’Eu, cắt Ox tại A(-4; 0) và B(-2;0).
Đồ thị hàm số y = g(x) là đường gấp khúc v’Cv, cắt Ox tại \(C({m \over 2};0)\)
Khi m thay đổi, điểm C chạy trên Ox; tia Cv luông song song với đường thẳng y = 2x; tia Cv’ luôn song song với đường thẳng y = -2x.

b) Bất phương trình đã cho đúng với mọi x khi và chỉ khi đồ thị của hàm số y = g(x) nằm hoàn toàn phía trên đồ thị của hàm số y = f(x) hay C nằm giữa A và B nghĩa là \( – 4 < {m \over 2} < – 2 \Leftrightarrow – 8 < m < – 4\)
Đáp số: \( – 8 < m < – 4\)
