GIẢI CHI TIẾT Giải SBT Bài 4 Chương 4 – SBT Toán 7 TẬP 1 – Cánh diều
================
Giải bài 25 trang 113 SBT Toán 7 Cánh diều tập 1 – CD
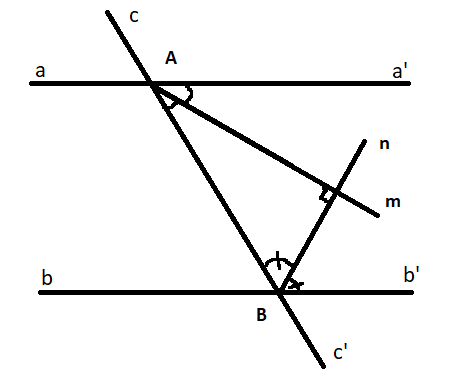
Cho định lí: “Nếu Am, Bn là hai tia phân giác của hai góc trong cùng phía tạo bởi một đường thẳng cắt hai đường thẳng song song thì Am vuông góc với Bn”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết, kết luận của định lí trên.
Phương pháp giải:
Giả thiết: Những dữ kiện đề bài cho
Kết luận: Điều cần chứng minh
Lời giải chi tiết:
a)

b)
|
GT |
aa’ // bb’, cc’ cắt aa’ tại A, cc’ cắt bb’ tại B Am là tia phân giác của góc a’Ac’ Bn là tia phân giác của góc b’Bc |
|
KL |
\(Am \bot Bn\) |
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 4
Giải bài 26 trang 113 SBT Toán 7 Cánh diều tập 1 – CD
Vẽ hình minh họa và viết giả thiết, kết luận của mỗi định lí sau:
a) Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng còn lại.
b) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
c) Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Phương pháp giải:
Dựa vào các định lí để vẽ hình minh họa, nêu giả thiết và kết luận.
Lời giải chi tiết:
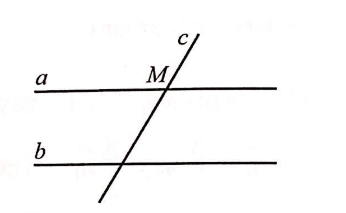
a)
|
GT |
a // b c cắt a tại G |
|
KL |
b, c cắt nhau |
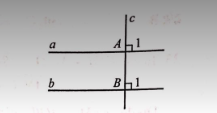
b)
|
GT |
a // b \(c \bot a\) |
|
KL |
\(c \bot b\) |
c)

|
GT |
a // c b // c |
|
KL |
a // b |
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 4
Giải bài 27 trang 113 SBT Toán 7 Cánh diều tập 1 – CD
Vẽ hình minh họa và viết giả thiết, kết luận của mỗi định lí sau:
a) Nếu hai góc nhọn xOy và mIn có Ox // Im, Oy // In thì hai góc đó bằng nhau;
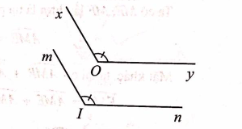
b) Nếu hai góc tù xOy và mIn có Ox // Im, Oy // In thì hai góc đó bằng nhau;
c) Nếu góc xOy nhọn, góc mIn tù có Ox // Im, Oy // In thì hai góc đó bù nhau.
Phương pháp giải:
Sử dụng dữ kiện của các định lí đã cho để vẽ hình minh họa, nêu giả thiết và kết luận.
Lời giải chi tiết:
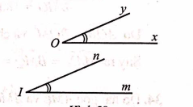
a)
|
GT |
\(\widehat {xOy},{\rm{ }}\widehat {mIn}\) là góc nhọn Ox // Im; Oy // In |
|
KL |
\(\widehat {xOy} = \widehat {mIn}\) |
b)
|
GT |
\(\widehat {xOy},{\rm{ }}\widehat {mIn}\) là góc tù Ox // Im; Oy // In |
|
KL |
\(\widehat {xOy} = \widehat {mIn}\) |
c)
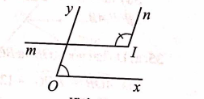
|
GT |
\(\widehat {xOy}\) là góc nhọn, \(\widehat {mIn}\) là góc tù Ox // Im; Oy // In |
|
KL |
\(\widehat {xOy} + \widehat {mIn} = 180^\circ \) |
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 4
Giải bài 28 trang 113 SBT Toán 7 Cánh diều tập 1 – CD
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thuyết, kết luận của định lí trên.
c) Chứng minh định lí trên.
Phương pháp giải:
Ta chứng minh các góc là góc vuông bằng cách chỉ ra số đo góc bằng 90 độ.
Lời giải chi tiết:
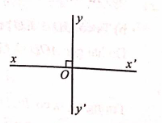
|
GT |
xx’ cắt yy’ tại O \(\widehat {xOy} = 90^\circ \) |
|
KL |
\(\widehat {x’Oy} = \widehat {x’Oy’} = \widehat {xOy’} = 90^\circ \) |
Chứng minh định lí:
Ta có: xx’ cắt yy’ tại O nên \(\widehat {xOy} + \widehat {x’Oy} = 180^\circ \) (hai góc kề bù) nên \(\widehat {x’Oy} = 180^\circ – \widehat {xOy} = 180^\circ – 90^\circ = 90^\circ \).
Mặt khác \(\widehat {xOy} = \widehat {x’Oy’};{\rm{ }}\widehat {xOy’} = \widehat {x’Oy}\) (các góc đối đỉnh) nên \(\widehat {x’Oy} = \widehat {x’Oy’} = \widehat {xOy’} = 90^\circ \).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 4
=============
