GIẢI CHI TIẾT Giải SBT Bài 3 Chương 4 – SBT Toán 7 TẬP 1 – Cánh diều
================
Giải bài 16 trang 110 SBT Toán 7 Cánh diều tập 1 – CD
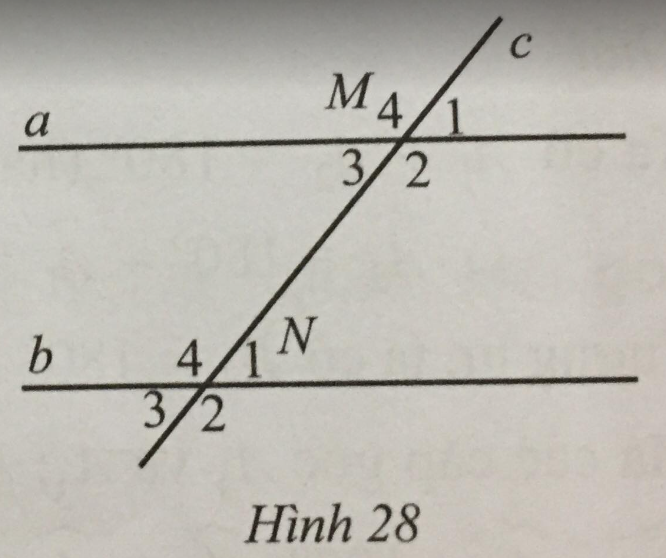
Quan sát Hình 28, biết a // b, \(\widehat {{M_3}} = 50^\circ \).

a) Nêu những cặp góc so le trong, những cặp góc đồng vị.
b) Tìm số đo mỗi góc còn lại của đỉnh M và N.
Phương pháp giải:
Tìm số đo các góc còn lại dựa vào số đo của góc đã cho và tính chất của hai đường thẳng song song: các góc đồng vị bằng nhau; so le trong (ngoài) bằng nhau; trong cùng phía bù nhau bằng nhau.
Lời giải chi tiết:
a) Những cặp góc so le trong là \(\widehat {{M_1}}\) và \(\widehat {{N_3}}\), \(\widehat {{M_2}}\) và \(\widehat {{N_4}}\), \(\widehat {{M_3}}\) và \(\widehat {{N_1}}\), \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\).
Những cặp góc đồng vị là \(\widehat {{M_1}}\) và \(\widehat {{N_1}}\), \(\widehat {{M_2}}\) và \(\widehat {{N_2}}\), \(\widehat {{M_3}}\) và \(\widehat {{N_3}}\), \(\widehat {{M_4}}\) và \(\widehat {{N_4}}\).
b) Ta có: Hai góc so le trong thì bằng nhau, hai góc đồng vị thì bằng nhau nên \(\widehat {{M_3}} = \widehat {{N_1}} = \widehat {{M_1}} = \widehat {{N_3}} = 50^\circ \).
Mà \({M_1}\) và \({M_4}\) là hai góc kề bù nhau nên \(\widehat {{M_1}} = \widehat {{M_4}} = 180^\circ \to \widehat {{M_4}} = 180^\circ – \widehat {{M_1}} = 180^\circ – 50^\circ = 130^\circ \).
Suy ra \({M_4} = {N_2} = {M_2} = {N_4} = 130^\circ \).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
Giải bài 17 trang 110 SBT Toán 7 Cánh diều tập 1 – CD
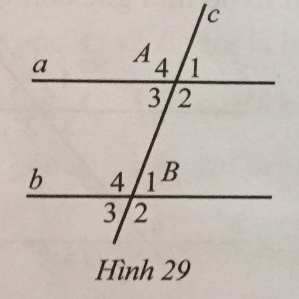
Quan sát Hình 29, biết a // b, \(3\widehat {{A_1}} = 2\widehat {{A_2}}\). Tìm số đo mỗi góc của đỉnh A và B.
Phương pháp giải:
Tính số đo mỗi góc của hai đỉnh dựa vào tính chất của hai đường thẳng song song: các góc đồng vị, so le trong (ngoài) bằng nhau; trong cùng phía bù nhau bằng nhau.
Lời giải chi tiết:
Ta có \(3\widehat {{A_1}} = 2\widehat {{A_2}}\) hay \(\widehat {{A_2}} = \dfrac{3}{2}\widehat {{A_1}}\) và \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (hai góc kề bù) nên
\(\begin{array}{l}\widehat {{A_1}} + \dfrac{3}{2}\widehat {{A_1}} = \dfrac{5}{2}\widehat {{A_1}} = 180^\circ \to \widehat {{A_1}} = 72^\circ \\ \Rightarrow \widehat {{A_2}} = \dfrac{3}{2}{\rm{ }}{\rm{. }}72^\circ = 108^\circ \end{array}\)
Mà a // b nên \(\widehat {{A_3}} = \widehat {{B_1}} = \widehat {{A_1}} = \widehat {{B_3}} = 72^\circ \) , \(\widehat {{A_4}} = \widehat {{B_2}} = \widehat {{A_2}} = \widehat {{B_4}} = 108^\circ \) (các góc so le trong và đồng vị).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
Giải bài 18 trang 110 SBT Toán 7 Cánh diều tập 1 – CD
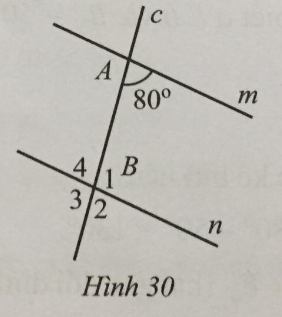
Tìm số đo mỗi góc \({B_1},{B_2},{B_3},{B_4}\) trong Hình 30, biết m //n.
Phương pháp giải:
Tính số đo mỗi góc của hai đỉnh dựa vào tính chất của hai đường thẳng song song: các góc đồng vị, so le trong (ngoài) bằng nhau; trong cùng phía bù nhau bằng nhau.
Lời giải chi tiết:
Ta có: m // n nên \(\widehat{B_4} = \widehat{B_2} = 80^\circ \) (hai góc so le trong và đồng vị với góc bằng 80°)
Mà \(\widehat{B_1} + \widehat{B_4} = 180^\circ \) (hai góc kề bù) nên \(\widehat{B_1} = \widehat{B_3} = 180^\circ – 80^\circ = 100^\circ \).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
Giải bài 19 trang 110 SBT Toán 7 Cánh diều tập 1 – CD
Quan sát Hình 31, biết \(\widehat {{P_3}}=\widehat {{Q_1}},\widehat {{M_3}} = 100^\circ \). Tìm số đo mỗi góc còn lại của đỉnh M và N.
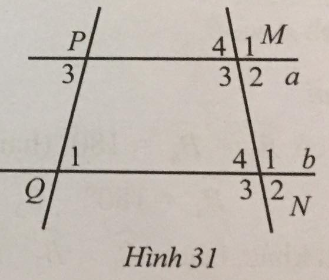
Phương pháp giải:
Để tính số đo mỗi góc còn lại của các đỉnh, ta cần chứng minh đường thẳng a song song với đường thẳng b.
Lời giải chi tiết:
Ta có: \(\widehat{P_3} = \widehat{Q_1}\). Mà 2 góc này ở vị trí so le trong nên nên a // b (Dấu hiệu nhận biết 2 đường thẳng song song)
Ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = 180^\circ \) (hai góc kề bù) nên \(\widehat {{M_4}} = 180^\circ – \widehat {{M_3}} = 180^\circ – 100^\circ = 80^\circ \).
Suy ra: \(\widehat {{M_3}} = \widehat {{N_1}} = \widehat {{M_1}} = \widehat {{N_3}} = 100^\circ \), \(\widehat {{M_4}} = \widehat {{N_2}} = \widehat {{M_2}} = \widehat {{N_4}} = 80^\circ \).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
Giải bài 20 trang 110 SBT Toán 7 Cánh diều tập 1 – CD
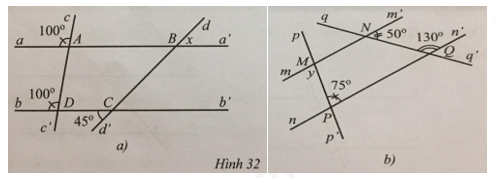
Tìm số đo x, y trong Hình 32.
Phương pháp giải:
Để tính số đo góc x, y, ta cần chứng minh đường thẳng a’ song song với đường thẳng b’ và đường thẳng m’ song song với đường thẳng n’.
Lời giải chi tiết:
a) Do \(\widehat {aAc} = \widehat {bDc}\) và chúng ở vị trí đồng vị nên aa’ // bb’ (Dấu hiệu nhận biết 2 đường thẳng song song)
Suy ra \(x = \widehat {bCd’} = 45^\circ \) (hai góc so le ngoài).
b) Ta có: \(\widehat {qNm’} + \widehat {m’Nq’} = 180^\circ \) (hai góc kề bù) nên \(\widehat {qNm’} = 180^\circ – \widehat {m’Nq’} = 180^\circ – 50^\circ = 130^\circ \).
Suy ra \(\widehat {qNm’} = \widehat {qQn’} = 130^\circ \). Mà 2 góc này ở vị trí đồng vị nên mm’ // nn’ (Dấu hiệu nhận biết 2 đường thẳng song song)
Vậy \(y = \widehat {pPn’} = 75^\circ \) (hai góc so le ngoài).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
Giải bài 21 trang 111 SBT Toán 7 Cánh diều tập 1 – CD
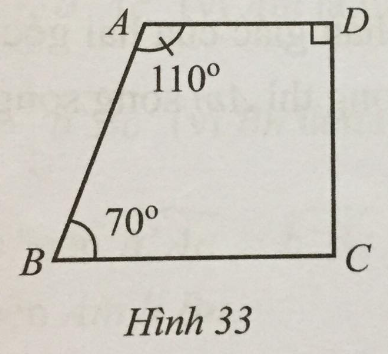
Tìm số đo góc BCD trong Hình 33.
Phương pháp giải:
Để tính số đo của góc BCD, ta cần chứng minh AD song song với BC.
Lời giải chi tiết:
Ta có: \(\widehat A + \widehat B = 110^\circ + 70^\circ = 180^\circ \) nên hai góc này bù nhau mà chúng ở vị trí trong cùng phía nên AD // BC.
Suy ra \(\widehat D + \widehat C = 180^\circ \) (hai góc trong cùng phía) nên \(\widehat {BCD} = 180^\circ – \widehat D = 180^\circ – 90^\circ = 90^\circ \).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
Giải bài 22 trang 111 SBT Toán 7 Cánh diều tập 1 – CD
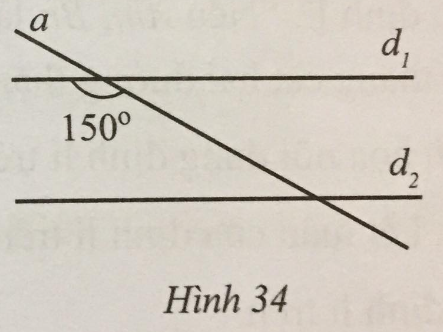
Quan sát Hình 34, biết \({d_1}\) // \({d_2}\) và góc tù tạo bởi hai đường thẳng a và đường thẳng \({d_1}\) bằng 150°. Tính góc nhọn tạo bởi đường thẳng a và đường thẳng \({d_2}\).
Phương pháp giải:
Ta tính góc nhọn tạo bởi hai đường thẳng dựa vào tính chất của hai đường thẳng song song: hai góc trong cùng phía bù nhau.
Lời giải chi tiết:
Ta có \({d_1}\) // \({d_2}\) nên góc tạo bởi đường thẳng a và đường thẳng \({d_1}\) với góc nhọn tạo bởi đường thẳng a và đường thẳng \({d_2}\) bù nhau.
Suy ra góc nhọn tạo bởi đường thẳng a và đường thẳng \({d_2}\) bằng \(180^\circ – 150^\circ = 30^\circ \).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
Giải bài 23 trang 111 SBT Toán 7 Cánh diều tập 1 – CD
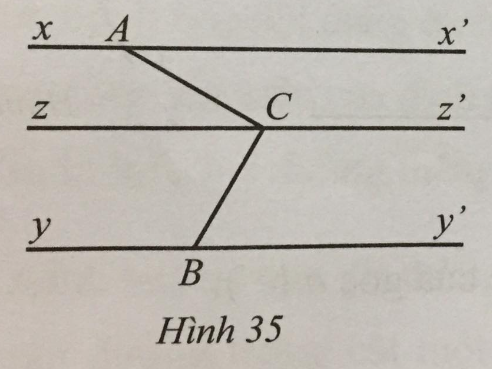
Quan sát Hình 35, biết xx’ // yy’ // zz’. Chứng tỏ rằng \(\widehat {ACB} = \widehat {CAx’} + \widehat {CBy’}\)
Phương pháp giải:
Ta chứng minh dựa vào tính chất của hai đường thẳng song song.
Lời giải chi tiết:
Do xx’ // zz’ nên \(\widehat {ACz} = \widehat {CAz’}\) (hai góc so le trong)
Do yy’ // zz’ nên \(\widehat {BCz} = \widehat {CBy’}\) (hai góc so le trong)
Vậy \(\widehat {ACB} = \widehat {ACz} + \widehat {BCz} = \widehat {CAx’} + \widehat {CBy’}\).
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
Giải bài 24* trang 111 SBT Toán 7 Cánh diều tập 1 – CD
Bạn Khôi vẽ hai đường thẳng a và b cắt nhau tại một điểm nằm ngoài phạm vi tờ giấy (Hình 36). Em hãy giúp bạn Khôi nêu cách đo góc nhọn tạo bởi hai đường thẳng a và b đã vẽ.
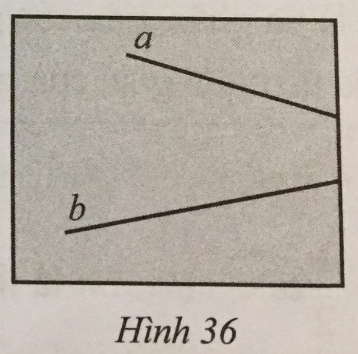
Phương pháp giải:
Ta đo góc nhọn cần đo bằng cách đo một góc nhọn khác bằng với nó.
Lời giải chi tiết:
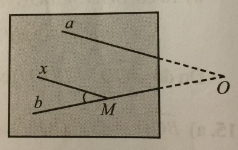
Lấy \(M \in b\). Kẻ Mx // a với \(\widehat {bMx} < 90^\circ \). Khi đó góc nhọn tạo bởi hai đường thẳng a và b đã vẽ chính là góc bMx vì chúng nằm ở vị trí đồng vị. Vậy ta chỉ cần đo góc bMx sẽ ra được góc nhọn tạo bởi hai đường thẳng a và b đã vẽ.
Giải bài tập Toán 7 Cánh diều Chương 4 Bài 3
=============
