Giải SBT Bài 3: Công thức lượng giác – Chương 6 – Đại số 10 - Sách Toán

Bài 3: Công thức lượng giác – Lời giải bài 16, 17, 18 trang 193; bài 19, 20, 21, 22 trang 194 Sách bài tập (SBT) Toán Đại số 10.

Bài 16 trang 193 SBT Toán Đại số 10

Cho $\cos \alpha = {1 \over 3}$ tính $sin(\alpha + {\pi \over 6}) – \cos (\alpha – {{2\pi } \over 3})$

Ta có:

$sin(\alpha + {\pi \over 6}) – \cos (\alpha – {{2\pi } \over 3})$

= $sin\alpha c{\rm{os}}{\pi \over 6} + \cos \alpha \sin {\pi \over 6} – \cos \alpha \cos {{2\pi } \over 3} – \sin \alpha \sin {{2\pi } \over 3}$

$ = {{\sqrt 3 } \over 2}sin\alpha + {1 \over 2}\cos \alpha + {1 \over 2}\cos \alpha – {{\sqrt 3 } \over 2}\sin \alpha $

$ = \cos \alpha = {1 \over 3}$

Bài 17 trang 193 SBT Toán Đại lớp 10

Cho $\sin \alpha = {8 \over {17}},\sin \beta = {{15} \over {17}}$ với $0 < \alpha < {\pi \over 3},0 < \beta < {\pi \over 2}$. Chứng minh rằng $\alpha + \beta = {\pi \over 2}$

Gợi ý làm bài

Ta có:

$\eqalign{
& \cos \alpha = \sqrt {1 – {{64} \over {289}}} = \sqrt {{{225} \over {289}}} = {{15} \over {17}}; \cr
& \cos \beta = \sqrt {1 – {{225} \over {289}}} = \sqrt {{{64} \over {289}}} = {8 \over {17}} \cr} $

Do đó:

$\sin (\alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $

${8 \over {17}}.{8 \over {17}} + {{15} \over {17}}.{{15} \over {17}} = {{289} \over {289}} = 1$

Vì $0 < \alpha < {\pi \over 3},0 < \beta < {\pi \over 2}$ nên từ đó suy ra $\alpha + \beta = {\pi \over 2}$

Bài 18 trang 193

Không dùng bảng số và máy tính, chứng minh rằng

a) $\sin {20^0} + 2\sin {40^0} – \sin {100^0} = \sin {40^0}$

b) ${{\sin ({{45}^0} + \alpha ) – c{\rm{os(}}{{45}^0} + \alpha )} \over {\sin ({{45}^0} + \alpha ) + c{\rm{os(}}{{45}^0} + \alpha )}} = \tan \alpha $

c) ${{3{{\cot }^2}{{15}^0} – 1} \over {3 – c{\rm{o}}{{\rm{t}}^2}{{15}^0}}} = – \cot {15^0}$

d) $\sin {200^0}\sin {310^0} + c{\rm{os34}}{{\rm{0}}^0}{\rm{cos5}}{{\rm{0}}^0}{\rm{ = }}{{\sqrt 3 } \over 2}$

Bài làm

$\eqalign{
& \sin {20^0} + 2\sin {40^0} – \sin {100^0} \cr
& = (\sin {20^0} – \sin {100^0}) + 2\sin {40^0} \cr} $

=$2\cos {60^0}\sin ( – {40^0}) + 2\sin {40^0}$

=$ – \sin {40^0} + 2\sin {40^0} = \sin {40^0}$

$\eqalign{
& {{\sin ({{45}^0} + \alpha ) – c{\rm{os(}}{{45}^0} + \alpha )} \over {\sin ({{45}^0} + \alpha ) + c{\rm{os(}}{{45}^0} + \alpha )}} \cr
& = {{\sin ({{45}^0} + \alpha ) – \sin {\rm{(}}{{45}^0} – \alpha )} \over {\sin ({{45}^0} + \alpha ) + \sin {\rm{(}}{{45}^0} – \alpha )}} \cr} $

=${{2\cos {{45}^0}\sin \alpha } \over {2\sin {{45}^0}\cos \alpha }} = {{\sqrt 2 \sin \alpha } \over {\sqrt 2 \cos \alpha }} = \tan \alpha $

${{3{{\cot }^2}{{15}^0} – 1} \over {3 – c{\rm{o}}{{\rm{t}}^2}{{15}^0}}} = {{{{\cot }^2}{{30}^0}{{\cot }^2}{{15}^0} – 1} \over {c{\rm{o}}{{\rm{t}}^2}{{30}^0} – {{\cot }^2}{{15}^0}}}$

=${{\cot {{30}^0}\cot {{15}^0} + 1} \over {c{\rm{ot}}{{30}^0} – \cot {{15}^0}}}.{{\cot {{30}^0}\cot {{15}^0} – 1} \over {c{\rm{ot}}{{30}^0} + \cot {{15}^0}}}$

Mặt khác ta có

$\cot (\alpha + \beta ) = {{\cos (\alpha + \beta )} \over {\sin (\alpha + \beta )}} = {{\cos \alpha \cos \beta – \sin \alpha \sin \beta } \over {\sin \alpha \cos \beta + \cos \alpha \sin \beta }}$

Chia cả tử và mẫu của biểu thức cho $\sin \alpha \sin \beta $ ta được

$\cot (\alpha + \beta ) = {{\cot \alpha \cot \beta – 1} \over {\cot \alpha + \cot \beta }}$

Tương tự

$\cot (\alpha – \beta ) = {{\cot \alpha \cot \beta + 1} \over {\cot \beta – \cot \alpha }}$

Do đó

$A = \cot ({15^0} – {30^0})\cot ({15^0} + {30^0}) = – \cot {15^0}$

$\sin {200^0}\sin {310^0} + c{\rm{os34}}{{\rm{0}}^0}{\rm{cos5}}{{\rm{0}}^0}$

= $\sin ({180^0} + {20^0})\sin ({360^0} – {50^0}) + c{\rm{os(36}}{{\rm{0}}^0}{\rm{ – 2}}{{\rm{0}}^0}{\rm{)cos5}}{{\rm{0}}^0}$

$ = ( – \sin {20^0})( – \sin {50^0}) + \cos {20^0}\cos {50^0}$

$ = \cos {50^0}\cos {20^0} + \sin {50^0}\sin {20^0}$

= $\cos ({50^0} – {20^0}) = {{\sqrt 3 } \over 2}$

Bài 19 trang 194 Sách bài tập (SBT) Toán lớp 10

Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc $\alpha ,\beta $

a) $\sin 6\alpha \cot 3\alpha – c{\rm{os6}}\alpha $

b) ${{\rm{[}}\tan ({90^0} – \alpha ) – \cot ({90^0} + \alpha ){\rm{]}}^2} – {{\rm{[}}c{\rm{ot(18}}{{\rm{0}}^0} + \alpha ) + \cot ({270^0} + \alpha ){\rm{]}}^2}$

c) $(\tan \alpha – \tan \beta )cot(\alpha – \beta ) – \tan \alpha \tan \beta $

d) $(\cot {\alpha \over 3} – \tan {\alpha \over 3})\tan {{2\alpha } \over 3}$

Lời giải

$\eqalign{
& \sin 6\alpha \cot 3\alpha – c{\rm{os6}}\alpha \cr
& = 2\sin 3\alpha \cos 3\alpha .{{\cos 3\alpha } \over {\sin 3\alpha }} – (2{\cos ^2}3\alpha – 1) \cr} $

= $2{\cos ^2}3\alpha – 2{\cos ^2}3\alpha + 1 = 1$

${{\rm{[}}\tan ({90^0} – \alpha ) – \cot ({90^0} + \alpha ){\rm{]}}^2} – {{\rm{[}}c{\rm{ot(18}}{{\rm{0}}^0} + \alpha ) + \cot ({270^0} + \alpha ){\rm{]}}^2}$

= ${(\cot \alpha + \tan \alpha )^2} – {(\cot \alpha – \tan \alpha )^2}$

= ${\cot ^2}\alpha + 2 + {\tan ^2}\alpha – {\cot ^2}\alpha + 2 – {\tan ^2}\alpha = 4$

$\eqalign{
& (\tan \alpha – \tan \beta )cot(\alpha – \beta ) – \tan \alpha \tan \beta \cr
& = {{\tan \alpha – \tan \beta } \over {\tan (\alpha – \beta )}} – \tan \alpha \tan \beta \cr} $

=$1 + \tan \alpha \tan \beta – \tan \alpha \tan \beta = 1$

$\eqalign{
& (\cot {\alpha \over 3} – \tan {\alpha \over 3})\tan {{2\alpha } \over 3} \cr
& = ({{\cos {\alpha \over 3}} \over {\sin {\alpha \over 3}}} – {{\sin {\alpha \over 3}} \over {\cos {\alpha \over 3}}}){{\sin {{2\alpha } \over 3}} \over {\cos {{2\alpha } \over 3}}} \cr} $

= $\eqalign{
& {{{{\cos }^2}{\alpha \over 3} – {{\sin }^2}{\alpha \over 3}} \over {\sin {\alpha \over 3}\cos {\alpha \over 3}}}.{{\sin {{2\alpha } \over 3}} \over {\cos {{2\alpha } \over 3}}} \cr
& = {{\cos {{2\alpha } \over 3}} \over {{1 \over 2}\sin {{2\alpha } \over 3}}}.{{\sin {{2\alpha } \over 3}} \over {\cos {{2\alpha } \over 3}}} = 2 \cr} $

Bài 20 trang 194 SBT Toán Đại lớp 10

Không sử dụng bảng số và máy tính, hãy tính

a) ${\sin ^4}{\pi \over {16}} + {\sin ^4}{{3\pi } \over {16}} + {\sin ^4}{{5\pi } \over {16}} + {\sin ^4}{{7\pi } \over {16}}$

b) $\cot 7,{5^0} + \tan 67,{5^0} – \tan 7,{5^0} – \cot 67,{5^0}$

Lời giải

a) ${\sin ^4}{\pi \over {16}} + {\sin ^4}{{3\pi } \over {16}} + {\sin ^4}{{5\pi } \over {16}} + {\sin ^4}{{7\pi } \over {16}}$

$ = {\left( {{{1 – \cos {\pi \over 8}} \over 2}} \right)^2} + {\left( {{{1 – \cos {{3\pi } \over 8}} \over 2}} \right)^2} + {\left( {{{1 – \cos {{5\pi } \over 8}} \over 2}} \right)^2} + {\left( {{{1 – \cos {{7\pi } \over 8}} \over 2}} \right)^2}$

$ = {1 \over 4}\left( {1 – 2\cos {\pi \over 8} + {{\cos }^2}{\pi \over 8} + 1 – 2\cos {{3\pi } \over 8} + {{\cos }^2}{{3\pi } \over 8} + 1 – 2\cos {{5\pi } \over 8} + {{\cos }^2}{{5\pi } \over 8} + 1 – 2\cos {{7\pi } \over 8} + {{\cos }^2}{{7\pi } \over 8}} \right)$

$ = 1 – {1 \over 2}\left( {\cos {\pi \over 8} + \cos {{3\pi } \over 8} + \cos {{5\pi } \over 8} + \cos {{7\pi } \over 8}} \right) + {1 \over 4}\left( {{{1 + \cos {\pi \over 4}} \over 2} + {{1 + \cos {{3\pi } \over 4}} \over 2} + {{1 + \cos {{5\pi } \over 4}} \over 2} + {{1 + \cos {{7\pi } \over 4}} \over 2}} \right)$$

=$1 – {1 \over 2}\left( {\cos {\pi \over 8} + \cos {{3\pi } \over 8} – \cos {{3\pi } \over 8} – \cos {\pi \over 8}} \right) + {1 \over 8}\left( {4 + {{\sqrt 2 } \over 2} – {{\sqrt 2 } \over 2} – {{\sqrt 2 } \over 2} + {{\sqrt 2 } \over 2}} \right)$

= ${3 \over 2}$

b) $\cot 7,{5^0} + \tan 67,{5^0} – \tan 7,{5^0} – \cot 67,{5^0}$

= ${{\cos 7,{5^0}} \over {\sin 7,{5^0}}} – {{\sin 7,{5^0}} \over {\cos 7,{5^0}}} + {{\sin 67,{5^0}} \over {\cos 67,{5^0}}} – {{\cos 67,{5^0}} \over {\sin 67,{5^0}}}$

= ${{{{\cos }^2}7,{5^0} – {{\sin }^2}7,{5^0}} \over {\sin 7,{5^0}\cos 7,{5^0}}} + {{{{\sin }^2}67,{5^0} – {{\cos }^2}67,{5^0}} \over {sin67,{5^0}\cos 67,{5^0}}}$

= $\eqalign{
& {{\cos {{15}^0}} \over {{1 \over 2}\sin {{15}^0}}} – {{\cos {{135}^0}} \over {{1 \over 2}\sin {{135}^0}}} \cr
& = {{2(\sin {{135}^0}\cos {{15}^0} – \cos {{135}^0}\sin {{15}^0})} \over {\sin {{15}^0}\sin {{135}^0}}} \cr} $

= ${{\sin ({{135}^0} – {{15}^0})} \over {\sin ({{45}^0} – {{30}^0})\sin ({{180}^0} – {{45}^0})}}$

= ${{2\sin {{120}^0}} \over {(\sin {{45}^0}\cos {{30}^0} – \cos {{45}^0}\sin {{30}^0})sin{{45}^0}}}$

$\eqalign{
& = {{\sqrt 3 } \over {{{\sqrt 2 } \over 2}({{\sqrt 3 } \over 2} – {1 \over 2}).{{\sqrt 2 } \over 2}}} \cr
& = {{4\sqrt 3 } \over {\sqrt 3 – 1}} = 6 + 2\sqrt 3 \cr} $$

Bài 21 trang 194

Rút gọn các biểu thức

a) ${{\sin 2\alpha + \sin \alpha } \over {1 + c{\rm{os2}}\alpha {\rm{ + cos}}\alpha }}$

b) ${{4{{\sin }^2}\alpha } \over {1 – c{\rm{o}}{{\rm{s}}^2}{\alpha \over 2}}}$

c) ${{1 + c{\rm{os}}\alpha – \sin \alpha } \over {1 – c{\rm{os}}\alpha – {\rm{sin}}\alpha }}$

d) ${{1 + \sin \alpha – 2{{\sin }^2}({{45}^0} – {\alpha \over 2})} \over {4c{\rm{os}}{\alpha \over 2}}}$

Bài làm

a) ${{\sin 2\alpha + \sin \alpha } \over {1 + c{\rm{os2}}\alpha {\rm{ + cos}}\alpha }} = {{\sin \alpha (2\cos \alpha + 1)} \over {2c{\rm{o}}{{\rm{s}}^2}\alpha {\rm{ + cos}}\alpha }}$

= ${{\sin \alpha (2\cos \alpha + 1)} \over {c{\rm{os}}\alpha (2{\rm{cos}}\alpha + 1)}} = \tan \alpha $

b) ${{4{{\sin }^2}\alpha } \over {1 – c{\rm{o}}{{\rm{s}}^2}{\alpha \over 2}}} = {{16{{\sin }^2}{\alpha \over 2}{{\cos }^2}{\alpha \over 2}} \over {{{\sin }^2}{\alpha \over 2}}} = 16{\cos ^2}{\alpha \over 2}$

c) ${{1 + c{\rm{os}}\alpha – \sin \alpha } \over {1 – c{\rm{os}}\alpha – {\rm{sin}}\alpha }} = {{2{{\cos }^2}{\alpha \over 2} – 2\sin {\alpha \over 2}\cos {\alpha \over 2}} \over {2si{n^2}{\alpha \over 2} – 2\sin {\alpha \over 2}\cos {\alpha \over 2}}}$

= ${{2\cos {\alpha \over 2}(\cos {\alpha \over 2} – \sin {\alpha \over 2})} \over {2\sin {\alpha \over 2}(sin{\alpha \over 2} – \cos {\alpha \over 2})}} = – \cot {\alpha \over 2}$

d) ${{1 + \sin \alpha – 2{{\sin }^2}({{45}^0} – {\alpha \over 2})} \over {4c{\rm{os}}{\alpha \over 2}}} = {{\sin \alpha + \cos ({{90}^0} – \alpha )} \over {4\cos {\alpha \over 2}}}$

=${{\sin \alpha + \sin \alpha } \over {4\cos {\alpha \over 2}}} = {{4\sin {\alpha \over 2}\cos {\alpha \over 2}} \over {4\cos {\alpha \over 2}}} = \sin {\alpha \over 2}$

Bài 22 trang 194 SBT Toán lớp 10

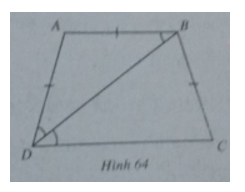
Cho hình thang cân ABCD có đáy nhỏ AB = AD. Biết $\tan \widehat {BDC} = {3 \over 4}$ tính các giá trị lượng giác của $\widehat {BAD}$

Gợi ý làm bài

Ta có (h.64)

$\widehat {ABD} = \widehat {ADB}$

$\widehat {ABD} = \widehat {BDC}$

=> $\widehat {BDC} = \widehat {ADB}$

Suy ra $\widehat {BAD} = \pi – 2\widehat {BDC}$

Từ đó ta có:

$\eqalign{
& \tan \widehat {BAD} = – \tan 2\widehat {BDC} = – {{2\tan \widehat {BDC}} \over {1 – {{\tan }^2}\widehat {BDC}}} \cr
& = – {{2.{3 \over 4}} \over {1 – {9 \over {16}}}} = – {3 \over 2}.{{16} \over 7} = – {{24} \over 7} \cr} $

Vì ${\pi \over 2} < \widehat {BAD} < \pi $ nên $\cos \widehat {BAD} < 0$. Do đó

$\eqalign{
& \cos \widehat {BAD} = – {1 \over {\sqrt {1 + {{\tan }^2}\widehat {BAD}} }} \cr
& = – {1 \over {\sqrt {1 + {{576} \over {49}}} }} = – {7 \over {25}} \cr} $

$\eqalign{
& \sin \widehat {BAD} = \cos \widehat {BAD}.\tan \widehat {BAD} \cr
& = {{ – 7} \over {25}}.{{ – 24} \over 7} = {{24} \over {25}} \cr} $