Giải SBT Bài 1 Chương 7 – SBT Toán 10 CHÂN TRỜI – GIẢI CHI TIẾT
===========
Giải bài 1 trang 8 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tính biệt thức và nghiệm (nếu có) của tam thức bậc hai sau. Xác định dấu của chúng tại \(x = – 2\)
a) \(f\left( x \right) = – 2{x^2} + 3x – 4\)
b) \(g\left( x \right) = 2{x^2} + 8x + 8\)
c) \(h\left( x \right) = 3{x^2} + 7x – 10\)
Phương pháp giải
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)\).
+ Nếu \(\Delta \) < 0 thi ƒ(x) cùng đấu với a với mọi giá trị x
+ Nếu \(\Delta \) = 0 và \({x_0} = – \frac{b}{{2{\rm{a}}}}\) là nghiệm kép của ƒ(x) thì ƒ(x) cùng dấu với a với mọi x khác x0.
+ Nếu \(\Delta \) > 0 và x1, x2 là hai nghiệm của \(f(x)\left( {{x_1} < {x_2}} \right)\) thì ƒ(x) trái dấu với a với mọi x trong.
Lời giải chi tiết
a) Biệt thức của f(x) là \(\Delta = {3^2} – 4.\left( { – 2} \right).\left( { – 4} \right) = – 23\)
Ta có \(\Delta < 0\) nên tam thức bậc hai đã cho vô nghiệm
\(f( – 2) = – 2.{( – 2)^2} + 3.( – 2) – 4 = – 18 < 0\) nên \(f(x)\) âm tại \(x = – 2\)
b) Biệt thức của g(x) là \(\Delta = {8^2} – 4.2.8 = 0\)
Ta có \(\Delta = 0\) nên tam thức bậc hai đã cho có nghiệm kép \({x_1} = {x_2} = – 2\)
Vậy nghiệm của g(x) là \( – 2\)
Do đó \(g( – 2) = 0\) nên \(g(x)\) không âm, không dương tại \(x = – 2\)
c) Biệt thức của h(x) là \(\Delta = {7^2} – 4.3.\left( { – 10} \right) = 169\)
Ta có \(\Delta > 0\) nên tam thức bậc hai đã cho có hai nghiệm là \(x = – \frac{{10}}{3}\) hoặc \(x = 1\)
Vậy nghiệm của h(x) là \( – \frac{{10}}{3}\) và 1
\(h( – 2) = 3.{( – 2)^2} + 7.( – 2) – 10 = – 12 < 0\) nên \(h(x)\) âm tại \(x = – 2\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 7 Bài 1
Giải bài 2 trang 9 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tìm giá trị của tham số m để:
a) \(f\left( x \right) = \left( {2m – 8} \right){x^2} + 2mx + 1\) là một tam thức bậc hai
b) \(f\left( x \right) = \left( {2m + 3} \right){x^2} + 3x – 4{m^2}\) là một tam thức bậc hai có \(x = 3\) là một nghiệm
c) \(f\left( x \right) = 2{x^2} + mx – 3\) dương tại \(x = 2\)
Phương pháp giải
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)\).
+ Nếu \(\Delta \) < 0 thi ƒ(x) cùng đấu với a với mọi giá trị x
+ Nếu \(\Delta \) = 0 và \({x_0} = – \frac{b}{{2{\rm{a}}}}\) là nghiệm kép của ƒ(x) thì ƒ(x) cùng dấu với a với mọi x khác x0.
+ Nếu \(\Delta \) > 0 và x1, x2 là hai nghiệm của \(f(x)\left( {{x_1} < {x_2}} \right)\) thì ƒ(x) trái dấu với a với mọi x trong.
Lời giải chi tiết
a) f(x) là tam thức bậc hai khi và chỉ khi \(2m – 8 \ne 0 \Leftrightarrow m \ne 4\)
Vậy để \(f\left( x \right)\) là tam thức bậc hai thì \(m \ne 4\)
b) f(x) là tam thức bậc hai khi và chỉ khi \(2m + 3 \ne 0 \Leftrightarrow m \ne – \frac{3}{2}\)
Mặt khác, \(x = 3\) là nghiệm của f(x) khi và chỉ khi \(f\left( 3 \right) = 0\)
hay \(f\left( 3 \right) = \left( {2m + 3} \right){.3^2} + 3.3 – 4{m^2} = 0 \Leftrightarrow – 4{m^2} + 18m + 36 = 0\)
Suy ra \(m = – \frac{3}{2}\) hoặc \(m = 6\)
Vậy để \(f\left( x \right)\) là tam thức bậc hai và có nghiệm là \(x = 3\) thì \(m = 6\)
c) Hàm số f(x) có \(a = 2 \ne 0\) nên là tam thức bậc hai
\(f\left( x \right) = 2{x^2} + mx – 3\) dương tại \(x = 2\) khi và chỉ khi \(f\left( 2 \right) > 0\)
hay \(f\left( 2 \right) = {2.2^2} + 2m – 3 > 0 \Leftrightarrow m > – \frac{5}{2}\)
Vậy để \(f\left( x \right)\) dương tại \(x = 2\) thì \(m > – \frac{5}{2}\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 7 Bài 1
Giải bài 3 trang 9 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tìm các giá trị của tham số m để:
a) \(f\left( x \right) = \left( {{m^2} + 9} \right){x^2} + \left( {m + 6} \right)x + 1\) là một tam thức bậc hai có một nghiệm duy nhất
b) \(f\left( x \right) = \left( {m – 1} \right){x^2} + 3x + 1\) là một tam thức bậc hai có hai nghiệm phân biệt
c) \(f\left( x \right) = m{x^2} + \left( {m + 2} \right)x + 1\) là một tam thức bậc hai vô nghiệm
Phương pháp giải
Sử dụng biệt thức delta \(\Delta = {b^2} – 4ac\)
Nếu \(\Delta < 0\) suy ra phương trình vô nghiệm
Nếu \(\Delta = 0\) suy ra phương trình có nghiệm kép
Nếu \(\Delta > 0\) suy ra phương trình hai nghiệm phân biệt
Lời giải chi tiết
a) Để \(f\left( x \right)\) là tam thức bậc hai thì \({m^2} + 9 \ne 0\) đúng với mọi \(m \in \mathbb{R}\)
Mặt khác, tam thức trên có một nghiệm duy nhất khi và chỉ khi \(\Delta = 0\)
hay \({\left( {m + 6} \right)^2} – 4.\left( {{m^2} + 9} \right) = 0 \Rightarrow – 3{m^2} + 12m = 0\) suy ra \(m = 0\) hoặc \(m = 4\)
Vậy khi \(m = 0\) hoặc \(m = 4\) thì \(f\left( x \right) = \left( {{m^2} + 9} \right){x^2} + \left( {m + 6} \right)x + 1\) là một tam thức bậc hai có một nghiệm duy nhất
b) Để \(f\left( x \right)\) là tam thức bậc hai thì \(m – 1 \ne 0 \Leftrightarrow m \ne 1\) (*)
Mặt khác, tam thức trên có hai nghiệm phân biệt khi và chỉ khi \(\Delta > 0\)
hay \({3^2} – 4.\left( {m – 1} \right) > 0 \Rightarrow – 4m + 13 > 0 \Leftrightarrow m < \frac{{13}}{4}\) (**)
Kết hợp (*) và (**) ta được \(m \in \left( { – \infty ;\frac{{13}}{4}} \right)\backslash 1\)
Vậy khi \(m \in \left( { – \infty ;\frac{{13}}{4}} \right)\backslash 1\) thì \(f\left( x \right) = \left( {m – 1} \right){x^2} + 3x + 1\) là một tam thức bậc hai có hai nghiệm phân biệt
c) Để \(f\left( x \right)\) là tam thức bậc hai thì \(m \ne 0\)
Mặt khác, tam thức trên vô nghiệm khi và chỉ khi \(\Delta < 0\)
hay \({\left( {m + 2} \right)^2} – 4m < 0 \Rightarrow {m^2} + 4 < 0\)
Ta có \({m^2} \ge 0\;\forall m \in \mathbb{R} \Rightarrow {m^2} + 4 \ge 4 > 0\;\forall m \in \mathbb{R}\),
Vậy không có giá trị m thỏa mãn yêu cầu bài toán
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 7 Bài 1
Giải bài 4 trang 9 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
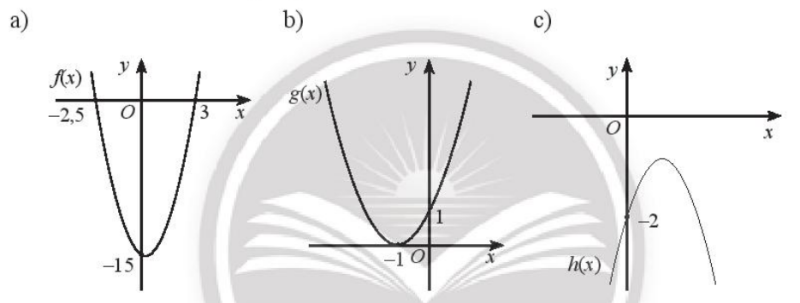
Dựa vào đồ thị của hàm số bậc hai được cho trong hình dưới đây, xét dấu của tam thức bậc hai tương ứng:

Phương pháp giải
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)\).
+ Nếu \(\Delta \) < 0 thi ƒ(x) cùng đấu với a với mọi giá trị x
+ Nếu \(\Delta \) = 0 và \({x_0} = – \frac{b}{{2{\rm{a}}}}\) là nghiệm kép của ƒ(x) thì ƒ(x) cùng dấu với a với mọi x khác x0.
+ Nếu \(\Delta \) > 0 và x1, x2 là hai nghiệm của \(f(x)\left( {{x_1} < {x_2}} \right)\) thì ƒ(x) trái dấu với a với mọi x trong.
Lời giải chi tiết
a) \(f\left( x \right) > 0\) dương trên khoảng \(\left( { – \infty ; – 2,5} \right)\) và \(\left( {3; + \infty } \right)\)
\(f\left( x \right) < 0\) âm trên khoảng \(\left( { – 2,5;3} \right)\)
b) \(g\left( x \right) > 0\) dương với mọi \(x \ne – 1\)
c) \(h\left( x \right) < 0\) âm với mọi \(x \in \mathbb{R}\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 7 Bài 1
Giải bài 5 trang 9 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Xét dấu của các tam thức bậc hai sau:
a) \(f\left( x \right) = {x^2} – 5x + 4\)
b) \(f\left( x \right) = – \frac{1}{3}{x^2} + 2x – 3\)
c) \(f\left( x \right) = 3{x^2} + 6x + 4\)
d) \(f\left( x \right) = – 2{x^2} + 3x + 5\)
e) \(f\left( x \right) = – 6{x^2} + 3x – 1\)
g) \(f\left( x \right) = 4{x^2} + 12x + 9\)
Phương pháp giải
Để xét dâu tam thức bậc hai \(f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)\), ta thực hiện các bước sau:
Bước 1: Tỉnh và xác định đâu của biệt thức \(\Delta \);
Bước 2: Xác định nghiệm của ƒ(x) (nếu có);
Bước 3: Xác định đâu của hệ sô a,
Bước 4: Xác định dâu của ƒ(x)
Lời giải chi tiết
a) f(x) dương trong khoảng \((-\infty; 1)\) và \((4; +\infty)\), f(x) âm trong khoảng (1; 4)
b) f(x) âm với mọi x \(\neq\) 3
c) f(x) dương với mọi x \(\in \mathbb{R}\)
d) f(x) âm trong khoảng \((-\infty; -1)\) và \((2,5; +\infty)\), f(x) dương trong khoảng (-1; 2,5)
e) f(x) âm với mọi x \(\in \mathbb{R}\)
g) f(x) dương với mợi x \(\neq \frac{-3}{2}\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 7 Bài 1
Giải bài 6 trang 9 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tìm các giá trị của tham số m để:
a) \(f\left( x \right) = \left( {m + 1} \right){x^2} + 5x + 2\) là tam thức bậc hai không đổi dấu trên \(\mathbb{R}\)
b) \(f\left( x \right) = m{x^2} – 7x + 4\) là tam thức bậc hai âm với mọi \(x \in \mathbb{R}\)
c) \(f\left( x \right) = 3{x^2} – 4x + \left( {3m – 1} \right)\) là tam thức bậc hai dương với mọi \(x \in \mathbb{R}\)
d) \(f\left( x \right) = \left( {{m^2} + 1} \right){x^2} – 3mx + 1\) là tam thức bậc hai âm với mọi \(x \in \mathbb{R}\)
Phương pháp giải
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)\).
+ Nếu \(\Delta \) < 0 thi ƒ(x) cùng đấu với a với mọi giá trị x
+ Nếu \(\Delta \) = 0 và \({x_0} = – \frac{b}{{2{\rm{a}}}}\) là nghiệm kép của ƒ(x) thì ƒ(x) cùng dấu với a với mọi x kháe x0.
+ Nến \(\Delta \) > 0 và x1, x2 là hai nghiệm của \(f(x)\left( {{x_1} < {x_2}} \right)\) thì ƒ(x) trái dấu với a với mọi x trong.
Lời giải chi tiết
a) \(f\left( x \right)\) là tam thức bậc hai khi và khi \(m + 1 \ne 0 \Leftrightarrow m \ne – 1\)
Mặt khác, để tam thức bậc hai không đổi dấu trên \(\mathbb{R}\) , tức là không cắt trục hoành (hay f(x)=0 vô nghiệm) khi và chỉ khi \(\Delta < 0\)
hay \({5^2} – 4\left( {m + 1} \right).2 < 0 \Leftrightarrow – 8m + 17 < 0 \Leftrightarrow m > \frac{{17}}{8}\)
Vậy để \(f\left( x \right) = \left( {m + 1} \right){x^2} + 5x + 2\) là tam thức bậc hai không đổi dấu trên \(\mathbb{R}\) thì \(m > \frac{{17}}{8}\)
b) \(f\left( x \right)\) là tam thức bậc hai khi và khi \(m \ne 0\)
Mặt khác, \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(a < 0\) và \(\Delta < 0\)
hay \(\left\{ \begin{array}{l}m < 0\\{\left( { – 7} \right)^2} – 4m.4 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\m > \frac{{49}}{{16}}\end{array} \right.\) (Vô lý)
Vậy không có giá trị nào của tham số m thỏa mãn yêu cầu.
c) \(f\left( x \right)\) có \(a = 3 > 0\), suy ra \(f\left( x \right)\) dương với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(\Delta < 0\)
hay \({\left( { – 4} \right)^2} – 4.3.\left( {3m – 1} \right) < 0 \Leftrightarrow – 36m + 28 < 0 \Leftrightarrow m > \frac{7}{9}\)
Vậy để \(f\left( x \right) = 3{x^2} – 4x + \left( {3m – 1} \right)\)là tam thức bậc hai dương với mọi \(x \in \mathbb{R}\) thì \(m > \frac{7}{9}\)
d) \(f\left( x \right) = \left( {{m^2} + 1} \right){x^2} – 3mx + 1\) có \(a = {m^2} + 1 > 0\forall m \in \mathbb{R}\)
mà để \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\) thì \(a < 0\) và \(\Delta < 0\)
Vậy không tồn tại giá trị m để \(f\left( x \right) = \left( {{m^2} + 1} \right){x^2} – 3mx + 1\) là tam thức bậc hai âm với mọi \(x \in \mathbb{R}\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 7 Bài 1
Giải bài 7 trang 10 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Chứng minh rằng
a) \(2{x^2} + \sqrt 3 x + 1 > 0\) với mọi \(x \in \mathbb{R}\)
b) \({x^2} + x + \frac{1}{4} \ge 0\) với mọi \(x \in \mathbb{R}\)
c) \( – {x^2} < – 2x + 3\) với mọi \(x \in \mathbb{R}\)
Phương pháp giải
a) Tam thức \(2{x^2} + \sqrt 3 x + 1\) có \(\Delta = {\left( {\sqrt 3 } \right)^2} – 4.2 = – 5 < 0\) và \(a = 2 > 0\)
b) Tam thức \({x^2} + x + \frac{1}{4}\) có \(\Delta = {1^2} – 4.\frac{1}{4} = 0\), có nghiệm kép \(x = – \frac{1}{2}\) và \(a = 1 > 0\)
c) \( – {x^2} < – 2x + 3\) với mọi \(x \in \mathbb{R}\) \( \Leftrightarrow {x^2} – 2x + 3 > 0\) với mọi \(x \in \mathbb{R}\)
Lời giải chi tiết
a) Tam thức \(2{x^2} + \sqrt 3 x + 1\) có \(\Delta = {\left( {\sqrt 3 } \right)^2} – 4.2 = – 5 < 0\) và \(a = 2 > 0\)
Suy ra \(2{x^2} + \sqrt 3 x + 1 > 0\forall x \in \mathbb{R}\) (đpcm)
b) Tam thức \({x^2} + x + \frac{1}{4}\) có \(\Delta = {1^2} – 4.\frac{1}{4} = 0\), có nghiệm kép \(x = – \frac{1}{2}\) và \(a = 1 > 0\)
Suy ra \({x^2} + x + \frac{1}{4} \ge 0\) với mọi \(x \in \mathbb{R}\) (đpcm)
c) \( – {x^2} < – 2x + 3\) với mọi \(x \in \mathbb{R}\) \( \Leftrightarrow {x^2} – 2x + 3 > 0\) với mọi \(x \in \mathbb{R}\)
Xét tam thức \({x^2} – 2x + 3\) ta có \(\Delta = {\left( { – 2} \right)^2} – 4.3 = – 8 < 0\) và \(a = 1 > 0\)
Suy ra \({x^2} – 2x + 3 > 0\) với mọi \(x \in \mathbb{R}\)\( \Leftrightarrow – {x^2} < – 2x + 3\) (đpcm)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 7 Bài 1
Giải bài 8 trang 10 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) trong mỗi trường hợp sau:
a) Đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( { – 1; – 4} \right),\left( {0;3} \right)\) và \(\left( {1; – 14} \right)\)
b) Đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( {0; – 2} \right),\left( {2;6} \right)\) và \(\left( {3;13} \right)\)
c) \(f\left( { – 5} \right) = 33,f\left( 0 \right) = 3\) và \(f\left( 2 \right) = 19\)
Phương pháp giải
Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)
a) Vì đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( { – 1; – 4} \right),\left( {0;3} \right)\) và \(\left( {1; – 14} \right)\) nên thay tọa độ của ba điểm vào phương trình tổng quát
b) Vì đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( {0; – 2} \right),\left( {2;6} \right)\) và \(\left( {3;13} \right)\) nên thay tọa độ của ba điểm vào phương trình tổng quát
Lời giải chi tiết
a) Vì đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( { – 1; – 4} \right),\left( {0;3} \right)\) và \(\left( {1; – 14} \right)\) nên thay tọa độ của ba điểm vào phương trình tổng quát ta có:
\(\left\{ \begin{array}{l} – 4 = a{\left( { – 1} \right)^2} + b\left( { – 1} \right) + c\\3 = a{.0^2} + b.0 + c\\ – 14 = a{\left( 1 \right)^2} + b\left( 1 \right) + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a – b + c = – 4\\c = 3\\a + b + c = – 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – 12\\b = – 5\\c = 3\end{array} \right.\)
Từ a, b, c đã xác định được ta có \(\Delta = 169 > 0\), tam thức có hai nghiệm phân biệt \(x = – \frac{3}{4}\) và \(x = \frac{1}{3}\), trong đó \(a = – 12 < 0\)
Ta có bảng biến thiên sau đây

Vậy tam thức đã cho có dạng là \(f\left( x \right) = – 12{x^2} – 5x + 3\) dương trên khoảng \(\left( { – \frac{3}{4};\frac{1}{3}} \right)\), âm trên khoảng \(\left( { – \infty ; – \frac{3}{4}} \right)\) và \(\left( {\frac{1}{3}; + \infty } \right)\)
b) Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)
Vì đồ thị của hàm số \(y = f\left( x \right)\) đi qua ba điểm có tọa độ là \(\left( {0; – 2} \right),\left( {2;6} \right)\) và \(\left( {3;13} \right)\)
nên thay tọa độ của ba điểm vào phương trình tổng quát ta có:
\(\left\{ \begin{array}{l} – 2 = a{.0^2} + b.0 + c\\6 = a{.2^2} + b.2 + c\\13 = a{.3^2} + b.3 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = – 2\\4a + 2b + c = 6\\9a + 3b + c = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = – 2\end{array} \right.\)
Từ a, b, c đã xác định được ta có \(\Delta = 12 > 0\), tam thức có hai nghiệm phân biệt \(x = – 1 – \sqrt 3 \) và \(x = – 1 + \sqrt 3 \), trong đó \(a = 1 > 0\)
Ta có bảng biến thiên sau đây

Vậy tam thức đã cho có dạng là \(f\left( x \right) = {x^2} + 2x – 2\) âm trên khoảng \(\left( { – 1 – \sqrt 3 ; – 1 + \sqrt 3 } \right)\), dương trên khoảng \(\left( { – \infty ; – 1 – \sqrt 3 } \right)\) và \(\left( { – 1 + \sqrt 3 ; + \infty } \right)\)
c) Giả sử tam thức bậc hai có công thức tổng quát là \(f\left( x \right) = a{x^2} + bx + c\)
Vì \(f\left( { – 5} \right) = 33\) nên \(a.{( – 5)^2} + b.( – 5) + c = 33\)
Vì \(f\left( 0 \right) = 3\) nên \(a{.0^2} + b.0 + c = 3\)
Vì \(f\left( 2 \right) = 19\) nên \(a{.2^2} + b.2 + c = 19\)
Từ đó ta có hệ
\(\left\{ \begin{array}{l}a.{( – 5)^2} + b.( – 5) + c = 33\\a{.0^2} + b.0 + c = 3\\a{.2^2} + b.2 + c = 19\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25a – 5b + c = 33\\c = 3\\4a + 2b + c = 19\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25a – 5b = 30\\4a + 2b = 16\\c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\\c = 3\end{array} \right.\)
Vậy \(f(x) = 2{x^2} + 4x + 3\), có \(\Delta ‘ = {2^2} – 2.3 = – 2 < 0\) và \(a = 2 > 0\)nên \(f(x) > 0\) với mọi \(x \in \mathbb{R}\).
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 7 Bài 1
===========
THUỘC: Giải sách bài tập Toán 10 – Chân trời
