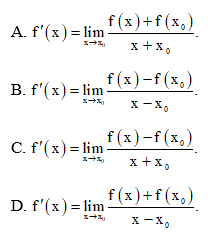
Giải Sách bài tập Toán 11 Bài 1 (Cánh diều): Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Giải Sách bài tập Toán 11 Bài 1 (Cánh diều): Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm – SÁCH GIÁO KHOA SGK Cánh diều 2024

================

Giải SBT Toán 11 Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Bài 1 trang 65 SBT Toán 11 Tập 2: Cho hàm số y = f(x) có đạo hàm x₀ là f’(x₀). Phát biểu nào sau đây là đúng?

Lời giải:

Đáp án đúng là: B

Hàm số y = f(x) có đạo hàm x₀ là f’(x₀) thì $f^{‘}\left(x\right)=\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}.$

Bài 2 trang 65 SBT Toán 11 Tập 2: Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t, Q = Q(t). Cường độ trung bình trong khoảng thời gian |t – t₀| được xác định bởi công thức $\frac{Q\left(t\right)-Q\left(t_0\right)}{t-t_0}.$Cường độ tức thời tại thời điểm t₀ là:

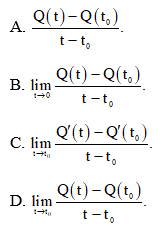
Lời giải:

Đáp án đúng là: D

Cường độ tức thời tại thời điểm t₀ là $\underset{t\to t_0}{\lim }\frac{Q\left(t\right)-Q\left(t_0\right)}{t-t_0}.$

Bài 3 trang 65 SBT Toán 11 Tập 2: Hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M₀(x₀; f(x₀)) là:

A. f(x₀).

B. f’(x₀).

C. x₀.

D. –f’(x₀).

Lời giải:

Đáp án đúng là: B

Hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M₀(x₀; f(x₀)) là: f’(x₀).

Bài 4 trang 65 SBT Toán 11 Tập 2: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M₀(x₀; f(x₀)) là:

A. y = f(x₀)(x – x₀) + f(x₀).

B. y = f’(x₀)(x + x₀) + f(x₀).

C. y = f’(x₀)(x – x₀) + f(x₀).

D. y = f’(x₀)(x – x₀) – f(x₀).

Lời giải:

Đáp án đúng là: C

Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M₀(x₀; f(x₀)) là:

y = f’(x₀)(x – x₀) + f(x₀).

Bài 5 trang 65 SBT Toán 11 Tập 2: Vận tốc tức thời của chuyển động s = f(t) tại thời điểm t₀ là:

A. f’(t₀).

B. f(t₀) – f’(t₀).

C. f(t₀).

D. – f’(t₀).

Lời giải:

Đáp án đúng là: A

Vận tốc tức thời của chuyển động s = f(t) tại thời điểm t₀ là: s’(t₀) = f’(t₀).

Bài 6 trang 65 SBT Toán 11 Tập 2: Tính đạo hàm của mỗi hàm số sau bằng định nghĩa:

a) f(x) = x + 2;

b) g(x) = 4x² – 1;

c) $h\left(x\right)=\frac{1}{x-1}.$

Lời giải:

a) Hàm số y = f(x) = x + 2.

Xét ∆x là số gia của biến số tại điểm x.

Ta có: ∆y = f(x + ∆x) – f(x) = (x + ∆x + 2) – (x + 2) = ∆x.

Suy ra $\frac{\Delta y}{\Delta x}=\frac{\Delta x}{\Delta x}=1$

Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }1=1$

Vậy f'(x) = 1.

b) Hàm số y = g(x) = 4x² – 1.

Xét ∆x là số gia của biến số tại điểm x.

Ta có: ∆y = g(x + ∆x) – g(x) = 4(x + ∆x)² – 1 – (4x² – 1)

= 4x² + 8x. ∆x + (∆x)² – 1 – 4x² + 1

= 8x.∆x + (∆x)².

Suy ra $\frac{\Delta y}{\Delta x}=\frac{8x\cdot \Delta x+{\left(\Delta x\right)}^2}{\Delta x}=8x+\Delta x.$

Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\left(8x+\Delta x\right)=8x.$

Vậy g'(x) = 8x.

c) Hàm số $y=h\left(x\right)=\frac{1}{x-1}.$

Xét ∆x là số gia của biến số tại điểm x.

Ta có: $\Delta y=h\left(x+\Delta x\right)-h\left(x\right)=\frac{1}{x+\Delta x-1}-\frac{1}{x-1}$

$=\frac{x-1-\left(x+\Delta x-1\right)}{\left(x+\Delta x-1\right)\left(x-1\right)}=\frac{-\Delta x}{\left(x+\Delta x-1\right)\left(x-1\right)}$

Suy ra $\frac{\Delta y}{\Delta x}=\frac{}{}\frac{-\Delta x}{\left(x+\Delta x-1\right)\left(x-1\right)}\Delta x=\frac{-1}{\left(x+\Delta x-1\right)\left(x-1\right)}.$

Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{-1}{\left(x+\Delta x-1\right)\left(x-1\right)}=\frac{-1}{{\left(x-1\right)}^2}.$

Vậy $h^{‘}\left(x\right)=\frac{-1}{{\left(x-1\right)}^2}.$

Bài 7 trang 65 SBT Toán 11 Tập 2: Chứng minh hàm số f(x) = |x – 2| không có đạo hàm tại điểm x₀ = 2, nhưng có đạo hàm tại mọi điểm x ≠ 2….

Lời giải:

Hàm số y = f(x) = |x – 2|.

• Với x > 2, ta có: f(x) = |x – 2| = x – 2.

Xét ∆x là số gia của biến số tại điểm x > 2.

Ta có: ∆y = f(x + ∆x) – f(x) = (x + ∆x – 2) – (x – 2) = ∆x.

Suy ra: $\frac{\text{Δ}y}{\text{Δ}x}=\frac{\text{Δ}x}{\text{Δ}x}=1.$

Ta thấy: $\underset{\Delta x\to 0}{\lim }\frac{\text{Δy}}{\text{Δ}x}=\underset{\Delta x\to 0}{\lim }1=1.$

Vậy đạo hàm của hàm số f(x) = |x – 2| tại điểm x > 2 là 1.

• Với x < 2, ta có: f(x) = |x – 2| = 2 – x.

Ta có: ∆y = f(x + ∆x) – f(x) = (2 – x – ∆x) – (2 – x) = –∆x.

Suy ra: $\frac{\text{Δ}y}{\text{Δ}x}=\frac{-\text{Δ}x}{\text{Δ}x}=-1.$

Ta thấy: $\underset{\Delta x\to 0}{\lim }\frac{\text{Δy}}{\text{Δ}x}=\underset{\Delta x\to 0}{\lim }\left(-1\right)=-1.$

Vậy đạo hàm của hàm số f(x) = |x – 2| tại điểm x < 2 là –1.

• Xét ∆x là số gia của biến số tại điểm x₀ = 2.

Ta có: ∆y = f(2 + ∆x) – f(2) = |2 + ∆x – 2| – |2 – 2| = ∆x.

Suy ra: $\frac{\text{Δ}y}{\text{Δ}x}=\frac{\left|\text{Δ}x\right|}{\text{Δ}x}$.

Ta thấy: $\underset{\Delta x\to 0^{+}}{\lim }\frac{\text{Δ}y}{\text{Δ}x}=\underset{\Delta x\to 0^{+}}{\lim }\frac{\left|\text{Δ}x\right|}{\text{Δ}x}=\underset{\Delta x\to 0^{+}}{\lim }\frac{\text{Δ}x}{\text{Δ}x}=1.$

$\underset{\text{Δ}x\to 0^{-}}{\text{lim}}\frac{\text{Δ}y}{\text{Δ}x}=\underset{\text{Δ}x\to 0^{-}}{\text{lim}}\frac{\left|\text{Δ}x\right|}{\text{Δ}x}=\underset{\text{Δ}x\to 0^{-}}{\text{lim}}\frac{-\text{Δ}x}{\text{Δ}x}=-1.$

Do đó, không tồn tại $\underset{\Delta x\to 0}{\lim }\frac{\text{Δ}f}{\text{Δ}x}$ nên hàm số không có đạo hàm tại điểm x₀ = 2.

Vậy hàm số f(x) = |x – 2| không có đạo hàm tại điểm x₀ = 2, nhưng có đạo hàm tại mọi điểm x ≠ 2.

Bài 8 trang 66 SBT Toán 11 Tập 2: Cho hàm số f(x) = x³ có đồ thị (C).

a) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng –1.

b) Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 8.

Lời giải:

Hàm số f(x) = x³.

Xét ∆x là số gia của biến số tại điểm x.

Ta có: ∆y = f(x + ∆x) – f(x) = (x + ∆x)³ – x³

= x³ + 3x².∆x + 3x(∆x)² + (∆x)³ – x³

= 3x².∆x + 3x(∆x)² + (∆x)³

= ∆x[3x² + 3x.∆x + (∆x)²]

Suy ra $\frac{\Delta y}{\Delta x}=\frac{\Delta x\cdot \left[3x^2+3x\cdot \Delta x+{\left(\Delta x\right)}^2\right]}{\Delta x}=3x^2+3x\cdot \Delta x+{\left(\Delta x\right)}^2.$

Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\left[3x^2+3x\cdot \Delta x+{\left(\Delta x\right)}^2\right]=3x^2+3x\cdot 0+0^2=3x^2.$

Vậy f'(x) = 3x².

a) Ta có f'(–1) = 3.(–1)² = 3 và f(–1) = (–1)³ = –1.

Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng –1 là:

y = f’(–1)(x – (–1)) + f(–1)

Hay y = 3(x + 1) – 1, tức là y = 3x + 2.

b) Gọi hoành độ của tiếp điểm có tung độ bằng 8 là x₀.

Do tiếp điểm thuộc (C), nên ta có:

f(x₀) = (x₀)³ = 8. Suy ra x₀ = 2.

Ta có: f'(2) = 3.2² = 12.

Vậy phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 8 là:

y = f’(2)(x – 2) + 8, hay y = 12(x – 2) + 8, tức là y = 12x – 16.

Bài 9 trang 66 SBT Toán 11 Tập 2: Một vật rơi tự do có phương trình chuyển động là $s\left(t\right)=\frac{1}{2}g{t}^2,$ trong đó g = 9,8 m/s²

a) Tìm vận tốc tức thời của vật tại thời điểm t = 3 (s).

b) Tìm thời điểm mà vận tốc tức thời của vật tại thời điểm đó bằng 39,2 (m/s).

Lời giải:

Xét ∆t là số gia của biến số tại điểm t.

Ta có:

$\text{Δ}s=s\left(t+\text{Δt}\right)-s\left(t\right)=\frac{1}{2}\cdot 9,8\cdot {\left(t+\text{Δt}\right)}^2-\frac{1}{2}\cdot 9,8\cdot t^2$

$=4,9t^2+9,8t\cdot \text{Δ}t+4,9{\left(\text{Δ}t\right)}^2-4,9t^2=\text{Δ}t\left(9,8t+4,9\text{Δt}\right).$

Suy ra: $\frac{\text{Δ}s}{\text{Δ}t}=\frac{\text{Δ}t\left(9,8t+4,9\text{Δt}\right)}{\text{Δ}t}=9,8t+4,9\text{Δ}t.$

Ta thấy: $\underset{\Delta t\to 0}{\lim }\frac{\text{Δ}s}{\text{Δ}t}=\underset{\Delta t\to 0}{\lim }\left(9,8t+4,9\text{Δ}t\right)=9,8t.$

Vậy v(t) = s’(t) = 9,8t (m/s).

a) Vận tốc tức thời của vật tại thời điểm t = 3 (s) là:

v(3) = 9,8.3 = 29,4 (m/s).

b) Theo đề bài, ta có: v(t) = 9,8t = 39,2, suy ra t = 4.

Vậy vận tốc tức thời của vật đạt 39,2 m/s tại thời điểm t = 4 (s).

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 6

Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Bài 2: Các quy tắc tính đạo hàm

=============
THUỘC: Giải SÁCH bài tập Toán 11 – SGK Cánh diều