Giải bài tập Cuối chương 9 (Toán 10 – Kết nối)

Giải bài tập Cuối chương 9 (Toán 10 – SGK Kết nối) KNTT
—————–

A. Trắc nghiệm:

Bài 9.13: Một hộp có bốn loại bi: bi xanh, bi đỏ, bi trắng và bi vàng. Lấy ngẫu nhiên ra một viên bi. Gọi E là biến cố: “Lấy được viên bi đỏ”. Biến cố đối của E là biến cố

A. Lấy được viên bi xanh.

B. Lấy được viên bi vàng hoặc bi trắng

C. Lấy được viên bi trắng.

D. Lấy được viên bi vàng hoặc bi trắng hoặc bi xanh.

Phương pháp giải

E và \(\overline E \) là hai biến cố đối khi và chỉ khi \(E \cup \overline E = \Omega \) và \(E \cap \overline E = \emptyset \)

Lời giải chi tiết

Chọn D.
Bài 9.14 : Rút ngẫu nhiên ra một thẻ từ một hộp có 30 tấm thẻ được đánh số từ 1 đến 30. Xác suất để số trên tấm thẻ được rút ra chia hết cho 5 là:

A. \(\frac{1}{{30}}\)

B. \(\frac{1}{5}\)

C. \(\frac{1}{3}\)

D. \(\frac{2}{5}\)

Phương pháp giải – Xem chi tiết

Các số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5.

Lời giải chi tiết

Số phần tử của không gian mẫu là\(n\left( \Omega \right) = 30\).

Gọi E là biến cố: “Số trên thẻ được rút ra là số chia hết cho 5”

Ta có \(E = \left\{ {5;10;15;20;25;30} \right\} \Rightarrow n\left( E \right) = 6\)

Vậy xác suất của biến cố E là \(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}} = \frac{1}{5}\).

Chọn B
Bài 9.15 : Gieo hai con xúc xắc cân đối. Xác suất để tổng số chấm xuất hiện trên hai con xúc xắc không lớn hơn 4 là:

A. \(\frac{1}{7}\)

B. \(\frac{1}{6}\)

C. \(\frac{1}{8}\)

D. \(\frac{2}{9}\)

Phương pháp giải – Xem chi tiết

Sử dụng công thức xác suất cổ điển \(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}}\).

Lời giải chi tiết

Số phần tử của không gian mẫu là \(n\left( \Omega \right) = 36\)

Gọi E là biến cố \(E = \left\{ {\left( {1,1} \right);\left( {1;2} \right);\left( {1,3} \right);\left( {2 & ;1} \right);\left( {2;2} \right);\left( {3,1} \right)} \right\}\) suy ra \(n\left( E \right) = 6\)

Vậy \(P\left( E \right) = \frac{6}{{36}} = \frac{1}{6}\).

Chọn B
Bài 9.16 : Một tổ trong lớp 10T có 4 bạn nữ và 3 bạn nam. Giáo viên chọn ngẫu nhiên hai bạn trong tổ đó tham gia đội làm báo của lớp. Xác suất để hai bạn được chọn có một bạn nam và một bạn nữ là:

A. \(\frac{4}{7}\)

B. \(\frac{2}{7}\)

C. \(\frac{1}{6}\)

D. \(\frac{2}{{21}}\)

Phương pháp giải

Sử dụng công thức xác suất cổ điển \(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}}\).

Lời giải chi tiết

Cách chọn 2 bạn từ 10 bạn là \(C_{10}^2 \Rightarrow n\left( \Omega \right) = C_{10}^2 = 21\)

Gọi A là biến cố: “Hai bạn được chọn có một bạn nam và một bạn nữ”.

Cách chọn một bạn nam là: 3 cách chọn

Cách chọn một bạn nữ là: 4 cách chọn

Theo quy tắc nhân ta có \(n\left( A \right) = 3.4 = 12\)

Vậy xác suất của biến cố A là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{12}}{{21}} = \frac{4}{7}\).

Chọn A

B. Tự luận:

Giải bài 9.17 trang 88 SGK Toán 10 Kết nối tri thức tập 2

Một hộp đựng bảy thẻ màu xanh đánh số từ 1 đến 7; năm thẻ màu đỏ đánh số từ 1 đến 5 và hai thẻ màu vàng đánh số từ 1 đến 2 . Rút ngẫu nhiên ra một tấm thẻ.

a) Mô tả không gian mẫu.

b) Mỗi biến cố sau là tập con nào của không gian mẫu?

A: “Rút ra được thẻ màu đỏ hoặc màu vàng”;

B: “Rút ra được thẻ mang số hoặc là 2 hoạc là 3 “.

Phương pháp giải

– Kí hiệu X là màu xanh, D là màu đỏ, V là màu vàng

– Tìm không gian mẫu

– Xác định các phần tử biến cố A, biến cố B

Lời giải chi tiết

a) Không gian mẫu: \(\Omega\) = {X1; X2; X3; X4; X5; X6; X7; D1; D2; D3; D4; D5; V1; V2}

=> \(n(\Omega )\) = 14.

b)

A= {X1; X2; X3; X4; X5; X6; X7; D1; D2; D3; D4; D5}.

B = {X2; X3; D2; D3; V2}.

Giải bài 9.18 trang 88 SGK Toán 10 Kết nối tri thức tập 2

Có hộp I và hộp II, mỗi hộp chứa 5 tấm thẻ đánh số từ 1 đến 5. Từ mỗi hộp, rút ngẫu nhiên ra một tấm thẻ. Tính xác suất để thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I.

Phương pháp giải

– Tìm \(n(\Omega )\)

– Gọi Biến cố A: “thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I”

– Tính n(A) => P(A)

Lời giải chi tiết

Rút từ hộp I có 5 cách, từ hợp II có 5 cách, số khả năng xảy ra khi rút mỗi hộp 1 thẻ là: 5.5 = 25, hay \(n(\Omega )\) = 25.

	1	2	3	4	5
1	11	12	13	14	15
2	21	22	23	24	25
3	31	32	33	34	35
4	41	42	43	44	45
5	51	52	53	54	55

Biến cố A: “thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I”.

A= {11; 12; 13 14; 15; 16; 23; 24; 25; 26; 34; 35; 36; 45; 46; 56}.

=> n(A) = 15

=> P(A) = \(\frac{15}{25}= \frac{3}{5}\).

Giải bài 9.19 trang 88 SGK Toán 10 Kết nối tri thức tập 2

Gieo đồng thời hai con xúc xắc cân đối. Tính xác suất đề:

a) Tổng số chấm trên hai con xúc xắc bằng 8;

b) Tồng số chấm trên hai con xúc xắc nhỏ hơn 8 .

Phương pháp giải

– Tính \(n(\Omega )\)

– Gọi Biến cố A: “Tổng số chấm trên hai con xúc xắc bằng 8”. Tính số kết quả thuận lợi với A

– Gọi Biến cố B: “Tổng số chấm trên hai con xúc xắc nhỏ hơn 8”.

+ Tính số chấm xúc xắc thứ hai khi số chấm của xúc xắc thứ nhất lần lượt là 1, 2, 3, 4, 5, 6

Lời giải chi tiết

Gieo hai con xúc xắc nên số kết quả có thể xảy ra là: 6.6 = 36, hay \(n(\Omega )\) = 36.

a) Biến cố A: “Tổng số chấm trên hai con xúc xắc bằng 8”.

Có 8 = 2 + 6 = 3 + 5 = 4 + 4. Nên số kết quả thuận lợi với A là: 5.

P(A) = \(\frac{5}{36}\).

b) Biến cố B: “Tổng số chấm trên hai con xúc xắc nhỏ hơn 8”.

+ Nếu số chấm của xúc xắc thứ nhất là 1 thì số chấm xúc xắc thứ hai có thể từ 1 đến 6: có 6 cách.

+ Nếu số chấm của xúc xắc thứ nhất là 2 thì số chấm xúc xắc thứ hai có thể từ 1 đến 5: có 5 cách.

+ Nếu số chấm của xúc xắc thứ nhất là 3 thì số chấm xúc xắc thứ hai có thể từ 1 đến 4: có 4 cách.

+ Nếu số chấm của xúc xắc thứ nhất là 4 thì số chấm xúc xắc thứ hai có thể từ 1 đến 3: có 3 cách.

+ Nếu số chấm của xúc xắc thứ nhất là 5 thì số chấm xúc xắc thứ hai có thể từ 1 đến 2: có 2 cách.

+ Nếu số chấm của xúc xắc thứ nhất là 6 thì số chấm xúc xắc thứ hai có thể từ 1: có 1 cách.

=> Số cách là: 6+5+4+3+2+1 = 21 cách, hay n(B) = 21.

=> P(B) = \(\frac{21}{36}=\frac{7}{12}\).

Giải bài 9.20 trang 89 SGK Toán 10 Kết nối tri thức tập 2

Dự báo thời tiết trong ba ngày thứ Hai, thứ Ba, thứ Tư của tuần sau cho biết, trong mỗi ngày này, khả năng có mưa và không mưa như nhau.

a) Vẽ sơ đồ hình cây mô tả không gian mẫu.

b) Tính xác suất của các biến cố:

F: “Trong ba ngày, có đúng một ngày có mưa”;

G: “Trong ba ngày, có ít nhất hai ngày không mưa”.

Phương pháp giải

– Vẽ hình sơ đồ hình cây, kí hiệu: M là mưa, KM là không mưa => \(n(\Omega )\)

– Dựa vào sơ đồ xác định số phần tử của các biến cố F, G. Từ đó ta tìm được P(F), P(G)

Lời giải chi tiết

a) Kí hiệu M là mưa, KM là không mưa.

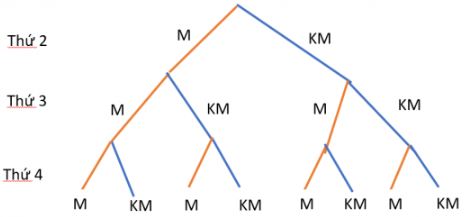
\(n(\Omega )\)= 8.

b)

+ Biến cố F:

Theo sơ đồ, n(F) = 3

=> P(F) = \(\frac{3}{8}\).

+ Biến cố G:

Theo sơ đồ, n(G) = 4

=> P(F) = \(\frac{4}{8}=\frac{1}{2}\).

Giải bài 9.21 trang 89 SGK Toán 10 Kết nối tri thức tập 2

Gieo một đồng xu cân đối liên tiếp bốn lần.

a) Vẽ sơ đồ hình cây mô tả không gian mẫu.

b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.

Phương pháp giải

– Vẽ hình sơ đồ hình cây, kí hiệu: S là mặt sấp, N là mặt ngửa => \(n(\Omega )\)

– Dựa vào sơ đồ xác định số phần tử của các biến cố A. Từ đó ta tìm được P(A)

Lời giải chi tiết

a) Kí hiệu S là mặt sấp, N là mặt ngửa.

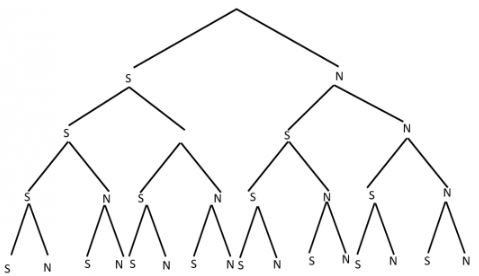
\(n(\Omega )\) = 16.

b) Biến cố A: “Trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.”

n(A) = 6

=> P(A) = \(\frac{6}{16}=\frac{3}{8}\).

Giải bài 9.22 trang 89 SGK Toán 10 Kết nối tri thức tập 2

Chọn ngẫu nhiên 4 viên bi từ một túi đựng 4 viên bi đỏ và 6 viên bi xanh đôi một khác nhau. Gọi A là biến cố: “Trong bốn viên bi đó có cả bi đỏ và cả bi xanh”. Tính P(A) và P(\(\overline{A}\)).

Phương pháp giải

– Chọn 4 viên bi từ 10 viên bi => \(n(\Omega )\)

– Tính số cách chọn với các trường hợp sau:

+ Trường hợp 1: có 1 xanh, 3 đỏ

+ Trường hợp 2: có 2 xanh, 2 đỏ

+ Trường hợp 3: có 3 xanh, 1 đỏ

– Sử dụng quy tắc cộng

Lời giải chi tiết

Chọn 4 viên bi từ 10 viên bi, thì số cách là: \(C_{10}^{4}\)= 210 cách.

=> \(n(\Omega )\) = 210.

Xét biến cố A, để có cả đỏ và xanh thì có các trường hợp sau:

+ Trường hợp 1: có 1 xanh, 3 đỏ, số cách là: 6.\(C_{4}^{3}\) = 24

+ Trường hợp 2: có 2 xanh, 2 đỏ, số cách là: \(C_{6}^{2}.C_{4}^{2}\) = 90.

+  Trường hợp 3: có 3 xanh, 1 đỏ, số cách là: \(C_{6}^{3}\).4 = 80.

=> n(A) = 24+90+80 = 194.

=> P(A) = \(\frac{194}{210}= \frac{97}{105}\).

=> P(\(\overline{A}\)) = 1 – P(A) = \(\frac{8}{105}\).