Giải bài tập Bài 19: Phương trình đường thẳng (Kết nối)

Giải bài tập Bài 19: Phương trình đường thẳng (Kết nối)
—————-

Giải bài 7.1 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Trong mặt phẳng tọa độ cho \(\overrightarrow{n}(2;1), \overrightarrow{v}(3; 2), A(1; 3), B(-2; 1)\)

a) Lập phương trình tổng quát của đường thẳng \(\Delta _{1}\) đi qua A và có vecto pháp tuyến \(\overrightarrow{n}\).

b) Lập phương trình tham số của đường thẳng \(\Delta _{2}\) đi qua B và có vecto chỉ phương \(\overrightarrow{v}\).

c) Lập phương trình tham số của đường thẳng AB.

Giải bài 7.1 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Trong mặt phẳng tọa độ cho \(\overrightarrow{n}(2;1), \overrightarrow{v}(3; 2), A(1; 3), B(-2; 1)\)

a) Lập phương trình tổng quát của đường thẳng \(\Delta _{1}\) đi qua A và có vecto pháp tuyến \(\overrightarrow{n}\).

b) Lập phương trình tham số của đường thẳng \(\Delta _{2}\) đi qua B và có vecto chỉ phương \(\overrightarrow{v}\).

c) Lập phương trình tham số của đường thẳng AB.

Phương pháp giải

– Phương trình tổng quát dạng ax + by + c =0, nhận \(\overrightarrow n \left( {a;b} \right)\) là một vectơ pháp tuyến.

– Đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u \left( {a;b} \right)\). Phương trình tham số của đường thẳng \(\Delta \) là \(\left\{ \begin{array}{l}
x = {x_0} + at\\
y = {y_0} + bt
\end{array} \right.\;\;\;\;\;\;\;\;\)

Lời giải chi tiết

a) Phương trình tổng quát của đường thẳng \(\Delta _{1}\) đi qua A và có vecto pháp tuyến $\overrightarrow{n}$:

2(x – 1) + 1.(y – 3) = 0 hay  2x + y -5 = 0.

b) Phương trình tham số của đường thẳng \(\Delta _{2}\) đi qua B và có vecto chỉ phương $\overrightarrow{v}$.

\(\left\{\begin{matrix}x=-2+3t\\ y=1+2t\end{matrix}\right.\)

c) Đường thẳng AB có vecto chỉ phương: \(\overrightarrow{AB}(-3; -2)\).

=> Chọn vecto chỉ phương: \(\overrightarrow{u}(3; 2)\).

Phương trình tham số của đường thẳng AB:

\(\left\{\begin{matrix}x=-2+3t\\ y=1+2t\end{matrix}\right.\)

Giải bài 7.2 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Lập phương trình tổng quát của các trục tọa độ

Giải bài 7.2 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Lập phương trình tổng quát của các trục tọa độ

Phương pháp giải

Phương trình tổng quát dạng ax + by + c =0, nhận \(\overrightarrow n \left( {a;b} \right)\) là một vectơ pháp tuyến.

Lời giải chi tiết

+) trục Ox: có vecto pháp tuyến \(\overrightarrow{n}(0; 1)\), đi qua điểm O(0; 0).

Phương trình tổng quát của đường thẳng chứa trục Ox: y = 0

+ trục Oy: có vecto pháp tuyến \(\overrightarrow{n}(1; 0)\), đi qua điểm O(0; 0).

Phương trình tổng quát của đường thẳng chứa trục Oy: x = 0

Giải bài 7.3 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Cho hai đường thẳng \(\Delta _{1}:\left\{\begin{matrix}x=1+2t\\ y=3+5t\end{matrix}\right.\) và 2x + 3y – 5 = 0.

a) Lập phương trình tổng quát của \(\Delta _{1}\)

b) Lập phương trình tham số của \(\Delta _{2}\)

Giải bài 7.3 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Cho hai đường thẳng \(\Delta _{1}:\left\{\begin{matrix}x=1+2t\\ y=3+5t\end{matrix}\right.\) và 2x + 3y – 5 = 0.

a) Lập phương trình tổng quát của \(\Delta _{1}\)

b) Lập phương trình tham số của \(\Delta _{2}\)

Phương pháp giải

– Phương trình tổng quát dạng ax + by + c =0, nhận \(\overrightarrow n \left( {a;b} \right)\) là một vectơ pháp tuyến.

– Đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u \left( {a;b} \right)\). Phương trình tham số của đường thẳng \(\Delta \) là \(\left\{ \begin{array}{l}
x = {x_0} + at\\
y = {y_0} + bt
\end{array} \right.\;\;\;\;\;\;\;\;\)

Lời giải chi tiết

a) \(\Delta _{1}\) có vecto chỉ phương \(\overrightarrow{u}(2;5)\)

=> \(\Delta _{1}\) có vecto pháp tuyến \(\overrightarrow{n}(5;-2)\)

Phương trình tổng quát: 5(x – 1) – 2(y – 3) = 0, hay 5x – 2y +1 = 0.

b) \(\Delta _{2}\) có vecto pháp tuyến \(\overrightarrow{n}(2;3)\)

=> \(\Delta _{2}\) có vecto chỉ phương \(\overrightarrow{n}(3;-2)\)

\(\Delta _{2}\) đi qua điểm có tọa độ: (1; 1)

Phương trình tham số: \(\left\{\begin{matrix}x=1+3t\\ y=1-2t\end{matrix}\right.\)

Giải bài 7.4 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 2), B(3; 0) và C(-2; -1).

a) Lập phương trình đường cao kẻ từ A.

b) Lập phương trình đường trung tuyến kẻ từ B.

Giải bài 7.4 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 2), B(3; 0) và C(-2; -1).

a) Lập phương trình đường cao kẻ từ A.

b) Lập phương trình đường trung tuyến kẻ từ B.

Phương pháp giải

– Phương trình tổng quát dạng ax + by + c =0, nhận \(\overrightarrow n \left( {a;b} \right)\) là một vectơ pháp tuyến.

– Đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u \left( {a;b} \right)\). Phương trình tham số của đường thẳng \(\Delta \) là \(\left\{ \begin{array}{l}
x = {x_0} + at\\
y = {y_0} + bt
\end{array} \right.\;\;\;\;\;\;\;\;\)

Lời giải chi tiết

a) Phương trình đường cao kẻ từ A của tam giác ABC nhận vecto \(\overrightarrow{BC}(-5; -1)\) làm vecto pháp tuyển.

=> Phương trình đường cao qua A và có vecto pháp tuyển \(\overrightarrow{BC}(-5; -1)\) là:

-5(x – 1) – 1.(y – 2) = 0 Hay 5x + y – 7 = 0.

b) Gọi M(x; y) là trung điểm của AC. Suy ra tọa độ điểm M là: \(\left\{\begin{matrix}x=\frac{1-2}{2}=\frac{-1}{2}\\ y=\frac{2-1}{2}=\frac{1}{2}\end{matrix}\right.\Rightarrow M\left ( \frac{-1}{2};\frac{1}{2} \right )\)

+ phương trình đường trung tuyến kẻ từ B có vecto chỉ phương là \(\overrightarrow{BM}(-3,5; 0,5)\)

=> Chọn một vecto chỉ phương của đường thẳng là: \(\overrightarrow{u}(-7; 1)\)

Phương trình tham số của đường thẳng qua B có vecto chỉ phương  \(\overrightarrow{u}(-7; 1)\):

\(\left\{\begin{matrix}x=3-7t\\ y=t\end{matrix}\right.\)

Giải bài 7.5 trang 34 SGK Toán 10 Kết nối tri thức tập 2

(Phương trình đoạn chắn của đường thẳng)

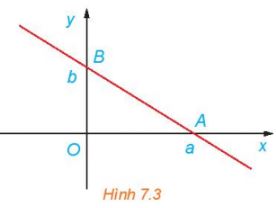
Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0) và B(0; b) với ab \(\neq \) 0 có phương trình là \(\frac{x}{a}+\frac{y}{b}=1\)

Giải bài 7.5 trang 34 SGK Toán 10 Kết nối tri thức tập 2

(Phương trình đoạn chắn của đường thẳng)

Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0) và B(0; b) với ab \(\neq \) 0 có phương trình là \(\frac{x}{a}+\frac{y}{b}=1\)

Phương pháp giải

– Tìm vectơ chỉ phương của đường thẳng AB => Vecto pháp tuyến.

=> Phương trình tổng quát của đường thẳng.

Lời giải chi tiết

Đường thẳng AB có vecto chỉ phương \(\overrightarrow{AB}(-a; b)\).

=> Đường thẳng có vecto pháp tuyến là: \(\overrightarrow{n}(b; a)\).

=> Phương trình tổng quát của đường thẳng là: b.(x – a) + a.(y – 0) = 0 hay b.x + a. y – ab = 0 (1)

Chia cả hai vế của (1) cho ab \(\neq \) 0 ta có: \(\frac{x}{a}+\frac{y}{b}=1\).

Vậy đường thẳng đi qua hai điểm A(a; 0) và B(0; b) với ab \(\neq \) 0 có phương trình là \(\frac{x}{a}+\frac{y}{b}=1\)

Giải bài 7.6 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Theo Google Maps, sân bay Nội Bài có vĩ độ 21,2^o Bắc, kinh độ 105,8^o Đông, sân bay Đà Nẵng có vĩ độ 16,1^o Bắc, kinh độ 108,2^o Đông. Một máy bay, bay từ Nội Bài đến sân bay Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ x^o Bắc, kinh độ y^o Đông được tính theo công thức

\(\left\{\begin{matrix}x=21,2-\frac{153}{40}t\\ y=105,8+\frac{9}{5}t\end{matrix}\right.\)

a) Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?

b) Tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến 17 (17^o Bắc) chưa?

Giải bài 7.6 trang 34 SGK Toán 10 Kết nối tri thức tập 2

Theo Google Maps, sân bay Nội Bài có vĩ độ 21,2^o Bắc, kinh độ 105,8^o Đông, sân bay Đà Nẵng có vĩ độ 16,1^o Bắc, kinh độ 108,2^o Đông. Một máy bay, bay từ Nội Bài đến sân bay Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ x^o Bắc, kinh độ y^o Đông được tính theo công thức

\(\left\{\begin{matrix}x=21,2-\frac{153}{40}t\\ y=105,8+\frac{9}{5}t\end{matrix}\right.\)

a) Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?

b) Tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến 17 (17^o Bắc) chưa?

Phương pháp giải

a) Nếu máy bay đến Đà Nẵng thì x = 16,1 và y = 108,2. Thay vào phương trình đã cho tìm được t

b) Tại thời điểm 1 giờ thì t = 1. Thay vào phương trình đã cho tìm được kết quả

Lời giải chi tiết

a) Nếu máy bay đến Đà Nẵng thì x = 16,1 và y = 108,2.

Ta có: \(\left\{\begin{matrix}16,1=21,2-\frac{153}{40}t\\ 108,2=105,8+\frac{9}{5}t\end{matrix}\right.\)

\(\Leftrightarrow t=\frac{4}{3}\)

Vậy chuyến bay từ Hà Nội đến Đà Nẵng mất gần 1,33 giờ.

b) Tại thời điểm 1 giờ thì t = 1 thay vào phương trình có:

\(\left\{\begin{matrix}x=21,2-\frac{153}{40}.1=17,375\\ y=105,8+\frac{9}{5}.1=107,6\end{matrix}\right.\)

Vậy tại thời điểm 1 giờ, máy bay đã qua vĩ tuyến 17.