Giải bài tập Bài 1. Giá trị lượng giác của một góc từ 0 đến 180. Định lí cosin và định lí sin trong tam giác (C4 – Toán 10 Cánh diều)
Giải bài tập Bài 1 trang 71 SGK Toán 10 Cánh diều tập 1
Cho tam giác ABC có \(AB = 3,5;\;AC = 7,5;\;\widehat A = {135^o}.\) Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
Phương pháp giải
Bước 1: Tính BC, bằng cách áp dụng định lí cosin trong tam giác ABC:
\({a^2} = {b^2} + {c^2} – 2bc.\cos A\)
Bước 2: Tính R, dựa vào định lí sin trong tam giác ABC:
\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{BC}}{{2.\sin A}}\)
Hướng dẫn giải
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} – 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} – 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)
Giải bài tập Bài 2 trang 71 SGK Toán 10 Cánh diều tập 1
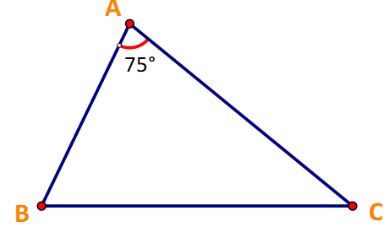
Cho tam giác ABC có \(\widehat B = {75^o},\widehat C = {45^o}\) và BC = 50. Tính độ dài cạnh AB.
Phương pháp giải
Bước 1: Tính \(\widehat A\)
Bước 2: Tính AB, bằng cách áp dụng định lí sin trong tam giác ABC:
Hướng dẫn giải
Ta có: \(\widehat B = {75^o},\widehat C = {45^o}\)\( \Rightarrow \widehat A = {180^o} – \left( {{{75}^o} + {{45}^o}} \right) = {60^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin {45^o}.\frac{{50}}{{\sin {{60}^o}}} \approx 40,8\)
Vậy độ dài cạnh AB là 40,8.
Giải bài tập Bài 3 trang 71 SGK Toán 10 Cánh diều tập 1
Cho tam giác ABC có \(AB = 6,AC = 7,BC = 8\). Tính \(\cos A,\sin A\) và bán kính R của đường trong ngoại tiếp tam giác ABC.
Phương pháp giải
Bước 1: Tính cosA, bằng cách áp dụng định lí cosin trong tam giác ABC:
\(B{C^2} = A{C^2} + A{B^2} – 2.AC.AB.\cos A\)
Bước 2: Tính sinA, dựa vào cos A.
Bước 3: Tính R, bằng cách áp dụng định lí sin trong tam giác ABC
\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{BC}}{{2.\sin A}}\)
Hướng dẫn giải
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} – 2.AC.AB.\cos A\)
\( \Rightarrow \cos A = \frac{{A{C^2} + A{B^2} – B{C^2}}}{{2.AB.AC}} = \frac{{{7^2} + {6^2} – {8^2}}}{{2.7.6}} = \frac{1}{4}\)
Lại có: \({\sin ^2}A + {\cos ^2}A = 1 \Rightarrow \sin A = \sqrt {1 – {{\cos }^2}A} \)(do \({0^o} < A \le {90^o}\))
\( \Rightarrow \sin A = \sqrt {1 – {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt {15} }}{4}\)
Áp dụng định lí sin trong tam giác ABC ta có:\(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{8}{{2.\frac{{\sqrt {15} }}{4}}} = \frac{{16\sqrt {15} }}{{15}}.\)
Vậy \(\cos A = \frac{1}{4};\)\(\sin A = \frac{{\sqrt {15} }}{4};\)\(R = \frac{{16\sqrt {15} }}{{15}}.\)
Giải bài tập Bài 4 trang 71 SGK Toán 10 Cánh diều tập 1
Tính giá trị đúng của các biểu thức sau (không dùng máy tính cầm tay):
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
b) \(B = \sin {5^o} + \sin {150^o} – \sin {175^o} + \sin {180^o}\)
c) \(C = \cos {15^o} + \cos {35^o} – \sin {75^o} – \sin {55^o}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
Phương pháp giải
a)
Bước 1: Tìm \(\cos {0^o};\cos {120^o}\) dựa vào bảng giá trị lượng giác của một số góc đặc biệt
Bước 2: Tính \(\cos {140^o}\) theo \(\cos {40^o}\) dựa vào công thức: \(\cos \alpha = – \cos \left( {{{180}^o} – \alpha } \right)\)
Bước 3: Rút gọn biểu thức.
b)
Bước 1: Tìm \(\sin {150^o};\sin {180^o}\) dựa vào bảng giá trị lượng giác của một số góc đặc biệt
Bước 2: Tính \(\sin {175^o}\) theo \(\sin {5^o}\) dựa vào công thức: \(\sin \alpha = \sin \left( {{{180}^o} – \alpha } \right)\)
Bước 3: Rút gọn biểu thức.
c)
Bước 1: Tính \(\sin {75^o}\) theo \(\cos {15^o}\) dựa vào công thức: \(\sin \alpha = \cos \left( {{{90}^o} – \alpha } \right)\)
Bước 2: Tính \(\sin {55^o}\) theo \(\cos {35^o}\) dựa vào công thức: \(\sin \alpha = \sin \left( {{{180}^o} – \alpha } \right)\)
Bước 3: Rút gọn biểu thức.
d)
Bước 1: Tính \(\tan {115^o}\) theo \(\tan {65^o}\) dựa vào công thức: \(\tan \alpha = – \tan \left( {{{180}^o} – \alpha } \right)\)
Bước 2: Tính \(\tan {65^o}\) theo \(\cot {25^o}\) dựa vào công thức: \(\tan \alpha = \cot \left( {{{90}^o} – \alpha } \right)\)
Bước 3: Rút gọn biểu thức.
e)
Bước 1: Tính \(\cot {100^o}\) theo \(\cot {80^o}\) dựa vào công thức: \(\cot \alpha = – \cot \left( {{{180}^o} – \alpha } \right)\)
Bước 2: Tính \(\cot {80^o}\) theo \(\tan {10^o}\) dựa vào công thức: \(\cot \alpha = \tan \left( {{{90}^o} – \alpha } \right)\)
Bước 3: Rút gọn biểu thức.
Hướng dẫn giải
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {0^o} = 1;\;\cos {120^o} = – \frac{1}{2}\)
Lại có: \(\cos {140^o} = – \cos \left( {{{180}^o} – {{40}^o}} \right) = – \cos {40^o}\)
\(\begin{array}{l} \Rightarrow A = 1 + \cos {40^o} + \left( { – \frac{1}{2}} \right) – \cos {40^o}\\ \Leftrightarrow A = \frac{1}{2}.\end{array}\)
b) \(B = \sin {5^o} + \sin {150^o} – \sin {175^o} + \sin {180^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\;\sin {180^o} = 0\)
Lại có: \(\sin {175^o} = \sin \left( {{{180}^o} – {{175}^o}} \right) = \sin {5^o}\)
\(\begin{array}{l} \Rightarrow B = \sin {5^o} + \frac{1}{2} – \sin {5^o} + 0\\ \Leftrightarrow B = \frac{1}{2}.\end{array}\)
c) \(C = \cos {15^o} + \cos {35^o} – \sin {75^o} – \sin {55^o}\)
Ta có: \(\sin {75^o} = \sin \left( {{{90}^o} – {{75}^o}} \right) = \cos {15^o}\); \(\sin {55^o} = \sin \left( {{{90}^o} – {{55}^o}} \right) = \cos {35^o}\)
\(\begin{array}{l} \Rightarrow C = \cos {15^o} + \cos {35^o} – \cos {15^o} – \cos {35^o}\\ \Leftrightarrow C = 0.\end{array}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
Ta có: \(\tan {115^o} = – \tan \left( {{{180}^o} – {{115}^o}} \right) = – \tan {65^o}\)
Mà: \(\tan {65^o} = \cot \left( {{{90}^o} – {{65}^o}} \right) = \cot {25^o}\)
\(\begin{array}{l} \Rightarrow D = \tan {25^o}.\tan {45^o}.\cot {25^o}\\ \Leftrightarrow D = \tan {45^o} = 1\end{array}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
Ta có: \(\cot {100^o} = – \cot \left( {{{180}^o} – {{100}^o}} \right) = – \cot {80^o}\)
Mà: \(\cot {80^o} = \tan \left( {{{90}^o} – {{80}^o}} \right) = \tan {10^o}\)
\(\begin{array}{l} \Rightarrow E = \cot {10^o}.\cot {30^o}.\tan {10^o}\\ \Leftrightarrow E = \cot {30^o} = \sqrt 3 .\end{array}\)
Giải bài tập Bài 5 trang 71 SGK Toán 10 Cánh diều tập 1
Cho tam giác ABC. Chứng minh:
a) \(\sin \frac{A}{2} = \cos \frac{{B + C}}{2}\)
b) \(\tan \frac{{B + C}}{2} = \cot \frac{A}{2}\)
Phương pháp giải
Bước 1: Tìm mối liên hệ giữa góc \(\frac{{\widehat A}}{2}\) và góc \(\frac{{\widehat B + \widehat C}}{2}\)
Bước 2: Áp dung: \(\sin \alpha = \cos \left( {{{90}^o} – \alpha } \right)\)và \(\tan \alpha = \cot \left( {{{90}^o} – \alpha } \right)\) suy ra đpcm.
Hướng dẫn giải
Xét tam giác ABC, ta có:
\(\widehat A + \widehat B + \widehat C = {180^o} \Rightarrow \frac{{\widehat A}}{2} + \frac{{\widehat B + \widehat C}}{2} = {90^o}\)
Do đó \(\frac{{\widehat A}}{2}\) và \(\frac{{\widehat B + \widehat C}}{2}\) là hai góc phụ nhau.
a) Ta có: \(\sin \frac{A}{2} = \cos \left( {{{90}^o} – \frac{A}{2}} \right) = \cos \frac{{B + C}}{2}\)
b) Ta có: \(\tan \frac{{B + C}}{2} = \cot \left( {{{90}^o} – \frac{{B + C}}{2}} \right) = \cot \frac{A}{2}\)
Giải bài tập Bài 6 trang 71 SGK Toán 10 Cánh diều tập 1
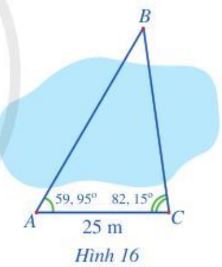
Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết AC = 25 m, \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\) Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Phương pháp giải
Bước 1: Tìm góc ABC.
Bước 2: Tính AB: Áp dụng định lí sin trong tam giác BAC: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
Hướng dẫn giải
Xét tam giác ABC, ta có: \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\)
\( \Rightarrow \widehat {ABC} = {180^o} – \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}\)
Áp dụng định lí sin trong tam giác BAC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin 59,{{95}^o}}} \approx 28,6\)
Vậy khoảng cách từ vị trí A đến vị trí B là 28,6 m.
Giải bài tập Bài 7 trang 71 SGK Toán 10 Cánh diều tập 1
Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc \({75^o}\). Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ và tàu thứ hai chạy với tốc độ 12 hải lí một giờ. Sau 2,5 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí (làm tròn kết quả đến hàng phần mười)?
Phương pháp giải
Bước 1: Quãng đường mỗi tàu đi được sau 2,5 giờ.
Bước 2: Tính khoảng cách giữa hai tàu bằng cách áp dụng định lí cosin.
Hướng dẫn giải
Gọi B, C lần lượt là vị trí của tàu thứ nhất và tàu thứ hai sau 2,5 giờ.
Sau 2,5 giờ:
Quãng đường tàu thứ nhất đi được là: AB = 8.2,5 = 20 (hải lí)
Quãng đường tàu thứ hai đi được là: AC = 12.2,5 = 30 (hải lí)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} – 2.AC.AB.\cos A\)
\(\begin{array}{l} \Rightarrow B{C^2} = {30^2} + {20^2} – 2.30.20.\cos {75^o}\\ \Rightarrow B{C^2} \approx 989,4\\ \Rightarrow BC \approx 31,5\end{array}\)
Vậy hai tàu cách nhau 31,5 hải lí.
Giải bài tập Bài 8 trang 71 SGK Toán 10 Cánh diều tập 1
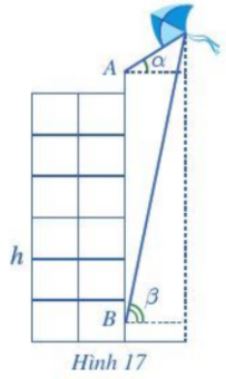
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là \(\alpha = {35^o}\); khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là \(\beta = {75^o}\); khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)?
Phương pháp giải
Bước 1: Vẽ hình, gọi các điểm O, C, D, H như hình vẽ.
Bước 2: Đặt x = OC. Tính AC, BD theo \(x,\alpha ,\beta \).
Bước 3: Lập luận tìm x. Từ đó suy ra khoảng cách OH.
Hướng dẫn giải
Gọi các điểm:
O là vị trí của chiếc diều.
H là hình chiếu vuông góc của chiếc diều trên mặt đất.
C, D lần lượt là hình chiếu vuông góc của A, B trên OH.
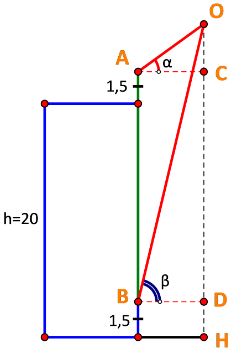
Đặt OC = x, suy ra OH = x + 20 + 1,5 =x + 21,5.
Xét tam giác OAC, ta có: \(\tan \alpha = \frac{{OC}}{{AC}} \Rightarrow AC = \frac{{OC}}{{\tan \alpha }} = \frac{x}{{\tan {{35}^o}}}\)
Xét tam giác OBD, ta có: \(\tan \beta = \frac{{OD}}{{BD}} \Rightarrow BD = \frac{{OD}}{{\tan \beta }} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
Mà:\(AC = BD\)\( \Rightarrow \frac{x}{{\tan {{35}^o}}} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
\(\begin{array}{l} \Leftrightarrow x.\tan {75^o} = \left( {x + 20} \right).\tan {35^o}\\ \Leftrightarrow x = \frac{{20.\tan {{35}^o}}}{{\tan {{75}^o} – \tan {{35}^o}}} \approx 4,6\end{array}\)
Suy ra OH = 26,1.
Vậy chiếc diều bay cao 26,1 m so với mặt đất.
