Giải Bài 4: Nhị thức Newton – Chuyên đề Toán 10 (Kết nối)

Giải Bài 4. Nhị thức Newton – Chuyên đề Toán 10 (Kết nối)
==========

Giải mục 1 trang 32, 33, 34 Chuyên đề học tập Toán 10

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Trong Bài 25 SGK Toán 10 (bộ sách Kết nối tri thức với cuộc sống), ta đã biết:

\({(a + b)^1} = a + b\)

\({(a + b)^2} = {a^2} + 2ab + {b^2}\)

\({(a + b)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\)

\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

\({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\)

Với \(n \in \left\{ {1;2;3;4;5} \right\}\) trong khai triển của mỗi nhị thức \({(a + b)^n}\):

a) Có bao nhiêu số hạng?

b) Tổng số mũ của a và b trong mỗi số hạng bằng bao nhiêu?

c) Số mũ của a và b thay đổi thế nào khi chuyển từ số hạng này đến số hạng tiếp theo, tính từ trái sangg phải?

Lời giải chi tiết:

Trong khai triển của mỗi nhị thức \({(a + b)^n}\):

a) Có \(n + 1\) số hạng.

b) Tổng số mũ của a và b trong mỗi số hạng luôn bằng n.

c) Số mũ của a giảm dần từ n về 0 khi chuyển từ số hạng này đến số hạng tiếp theo, tính từ trái sangg phải.

Số mũ của b tăng dần từ 0 đến n khi chuyển từ số hạng này đến số hạng tiếp theo, tính từ trái sangg phải.

Câu hỏi

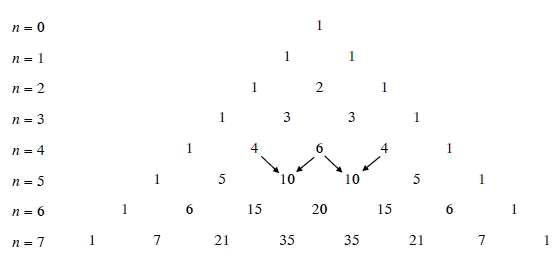
Tìm các hàng 7 và 8 của tam giác Pascal.

Lời giải chi tiết:

Ta đã có hàng 6 từ Hoạt động 2 trang 33:

\(\begin{array}{l}{(a + b)^6}\quad \quad 1\quad 6\quad 15\quad 20\quad 15\quad 6\quad 1\\{(a + b)^7}\quad \,1\quad 7\quad 21\quad 35\quad 35\quad 21\quad 7\quad 1\\{(a + b)^7}\;\;1\quad 8\quad 28\quad 56\quad 70\quad 56\quad 28\quad 8\quad 1\end{array}\)

Hàng 7: \(1 + 6 = 7,{\rm{ }}6 + 15 = 21,{\rm{ }}15 + 20 = 35\)

Hàng 8: \(1 + 7 = 8,{\rm{ 7}} + 21 = 28,{\rm{ 21 + 35 = 56,}}\;{\rm{35 + 35 = 70}}\)

Luyện tập 1

a) Sử dụng tam giác Pascal viết khai triển của \({(a + b)^7}\)

b) Sử dụng tam giác Pascal viết khai triển của \({(2x – 1)^4}\)

Phương pháp giải:

Dựa vào hàng tương ứng của tam giác Pascal

b) Viết khai triển của \({(a + b)^4}\)rồi thay \(a = 2x,b =  – 1\) vào khai triển nhận được.

Lời giải chi tiết:

a) Khai triển của \({(a + b)^7}\) có dạng

\({(a + b)^7} = {a^7} + ?{a^6}b + ?{a^5}{b^2} + ?{a^4}{b^3} + ?{a^3}{b^4} + ?{a^2}{b^5} + ?a{b^6} + ?{b^7}\)

Các hệ số trong khai triển này là các hệ số ở hàng 7 của tam giác Pascal. Do đó ta có ngay

\({(a + b)^7} = {a^7} + 7{a^6}b + 21{a^5}{b^2} + 35{a^4}{b^3} + 35{a^3}{b^4} + 21{a^2}{b^5} + 7a{b^6} + {b^7}\)

b) Ta viết khai triển của \({(a + b)^4}\)rồi thay \(a = 2x,b =  – 1\) vào khai triển nhận được.

Dựa vào hàng 4 của tam giác Pascal, ta có

\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

Với \(a = 2x,b =  – 1\) ta được:

\(\begin{array}{l}{(2x – 1)^4} = {\left( {2x} \right)^4} + 4.{\left( {2x} \right)^3}\left( { – 1} \right) + 6.{\left( {2x} \right)^2}{\left( { – 1} \right)^2} + 4.2x.{\left( { – 1} \right)^3} + {\left( { – 1} \right)^4}\\ = 16{x^4} – 32{x^3} + 24{x^2} – 8x + 1\end{array}\)

HĐ3

a) Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu:

\({(a + b)^1} = a + b = C_1^0a + C_1^1b\)

\({(a + b)^2} = {a^2} + 2ab + {b^2} = C_2^0{a^2} + C_2^1ab + C_2^2{b^2}\)

\({(a + b)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3} = C_3^0{a^3} + C_3^1{a^2}b + C_3^2a{b^2} + C_3^3{b^3}\)

\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4} = …\)

\({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5} = …\)

Nhận xét rằng các hệ số khai triển của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn \(C_4^1\) và \(C_4^3\), \(C_5^2\) và \(C_5^3\). Từ đó hãy dự đoán hệ thức giữa \(C_n^k\) và \(C_n^{n – k}(0 \le k \le n)\)

b) Từ tính chất của tam giác Pascal, hãy so sánh \(C_1^0 + C_1^1\) và \(C_2^1\), \(C_2^0 + C_2^1\) và \(C_3^1,…\) Từ đó hãy dự đoán hệ thức giữa \(C_{n – 1}^{k – 1} + C_{n – 1}^k\) và \(C_n^k.\)

Lời giải chi tiết:

a) \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4} = C_4^0{a^4} + C_4^1{a^3}b + C_4^2{a^2}{b^2} + C_4^3a{b^3} + C_4^4{b^4}\)

\(\begin{array}{l}{(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\\ = C_5^0{a^5} + C_5^1{a^4}b + C_5^2{a^3}{b^2} + C_5^3{a^2}{b^3} + C_5^4a{b^4} + C_5^5{b^5}\end{array}\)

Dễ thấy \(C_4^1 = C_4^3\) , \(C_5^2 = C_5^3\). Dự đoán \(C_n^k = C_n^{n – k}(0 \le k \le n)\)

b) Từ tính chất trong tam giác Pascal: Mọi số (khác 1) đều là tổng của hai số ở ngay phía trên nó.

Ta suy ra: \(C_1^0 + C_1^1 = C_2^1\), \(C_2^0 + C_2^1 = C_3^1\)

Dự đoán: \(C_{n – 1}^{k – 1} + C_{n – 1}^k = C_n^k.\)

Câu hỏi

Hãy chứng minh các công thức trên bằng cách sử dụng công thức tính số các tổ hợp

Phương pháp giải:

\(C_n^k = \frac{{n!}}{{k!\left( {n – k} \right)!}}\)

Lời giải chi tiết:

Tính chất đối xứng

\(C_n^k = \frac{{n!}}{{k!\left( {n – k} \right)!}} = \frac{{n!}}{{\left( {n – k} \right)!\left[ {n – (n – k)} \right]!}} = C_n^{n – k}\)

Hệ thức Pascal

\(\begin{array}{l}C_{n – 1}^{k – 1} + C_{n – 1}^k = \frac{{(n – 1)!}}{{(k – 1)!\left( {n – k} \right)!}} + \frac{{(n – 1)!}}{{k!\left( {n – 1 – k} \right)!}}\\ = \frac{{(n – 1)!}}{{(k – 1)!\left( {n – k – 1} \right)!}}\left( {\frac{1}{{n – k}} + \frac{1}{k}} \right)\\ = \frac{{(n – 1)!}}{{(k – 1)!\left( {n – k – 1} \right)!}}.\frac{n}{{(n – k).k}} = \frac{{n!}}{{k!\left( {n – k} \right)!}} = C_n^k\end{array}\)

Giải mục 2 trang 35, 36 Chuyên đề học tập Toán 10

Lựa chọn câu để xem lời giải nhanh hơn

HĐ4

Quan sát khai triển nhị thức của \({(a + b)^n}\) với \(n \in \left\{ {1;2;3;4;5} \right\}\) ở HDD3, hãy dự đoán công thức khai triển trong tường hợp tổng quát.

Lời giải chi tiết:

Quan sát khai triển nhị thức của \({(a + b)^n}\) với \(n \in \left\{ {1;2;3;4;5} \right\}\), ta thấy:

+ Công thức khai triển có n+1 số hạng,

+ Từ trái qua phải:

Hệ số khai triển của các số hạng lần lượt là \(C_n^0,C_n^1,…,C_n^n\).

Số mũ của a giảm dần từ n về 0.

Số mũ của b tăng dần từ 0 đến n.

=> Dự đoán \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Luyện tập 2

Khai triển \({(x – 2y)^6}\)

Phương pháp giải:

Áp dụng \({(a + b)^6} = C_6^0{a^6} + C_6^1{a^5}b + C_6^2{a^4}{b^2} + C_6^3{a^3}{b^3} + C_6^4{a^2}{b^4} + C_6^5a{b^5} + C_6^6{b^6}\)

Với \(a = x,b =  – 2y\)

Lời giải chi tiết:

Theo công thức nhị thức Newton, ta có:

\(\begin{array}{l}{(x – 2y)^6} = C_6^0{x^6} + C_6^1{x^5}.2y + C_6^2{x^4}{\left( {2y} \right)^2} + C_6^3{x^3}{\left( {2y} \right)^3} + C_6^4{x^2}{\left( {2y} \right)^4} + C_6^5x{\left( {2y} \right)^5} + C_6^6{\left( {2y} \right)^6}\\ = 1.{x^6} + 6.{x^5}.2y + 15.{x^4}.4{y^2} + 20{x^3}.8{y^3} + 15{x^2}16{y^4} + 6x.32{y^5} + 1.64{y^6}\\ = {x^6} + 12{x^5}y + 60{x^4}{y^2} + 160{x^3}{y^3} + 240{x^2}{y^4} + 192x{y^5} + 64{y^6}\end{array}\)

 

Luyện tập 3

Tìm hệ số của \({x^7}\) trong khai triển thành đa thức của \({(2 – 3x)^{10}}\)

Phương pháp giải:

Số hạng chứa \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{(ax)^k}{b^{n – k}}\)

Do đó hệ số của \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{a^k}{b^{n – k}}\)

Lời giải chi tiết:

Vì \({(2 – 3x)^{10}} = {( – 3x + 2)^{10}}\) nên

Số hạng chứa \({x^k}\) trong khai triển của \({(2 – 3x)^{10}}\) hay \({( – 3x + 2)^{10}}\)là \(C_{10}^{10 – k}{( – 3x)^k}{2^{10 – k}}\)

Số hạng chứa \({x^7}\) ứng với \(k = 7\), tức là số hạng \(C_{10}^3{( – 3x)^7}{2^3}\) hay \( – 2099520{x^7}\)

Vậy hệ số của \({x^7}\) trong khai triển của \({(2 – 3x)^{10}}\) là \( – 2099520\)

 

Vận dụng

a) Viết khai triển nhị thức Newton của \({(1 + x)^n}\)

b) Cho \(x = 1\) trong khai triển ở câu a), viết đẳng thức nhận được. Giải thích ý nghĩa của đẳng thức này với lưu ý rằng \(C_n^k(0 \le k \le n)\) chính là số tập con gồm k phần tử của một tập hợp có n phần tử.

c) Tương tự, cho \(x =  – 1\) trong khai triển ở câu a), viết đẳng thức nhận được. Giải thích ý nghĩa của đẳng thức này.

Lời giải chi tiết:

a) \({(1 + x)^n} = C_n^0 + C_n^1x + C_n^2{x^2} + … + C_n^n{x^n}\)

b) Thay \(x = 1\) trong khai triển ở câu a), ta được:

\({2^n} = C_n^0 + C_n^1 + C_n^2 + … + C_n^n\)

Với \(C_n^k(0 \le k \le n)\) chính là số tập con gồm k phần tử của một tập hợp có n phần tử, thì vế phải là tổng số tập con của tập hợp có n phần tử.

=> Số tập con của tập có n phần tử là: \({2^n}\)

c) Thay \(x =  – 1\) trong khai triển ở câu a), ta được:

\(\begin{array}{l}0 = C_n^0 – C_n^1 + C_n^2 + … + {( – 1)^n}C_n^n{x^n}\\ \Leftrightarrow C_n^0 + C_n^2 + C_n^4 + … = C_n^1 + C_n^3 + C_n^5 + …\end{array}\)

Ý nghĩa: Tập hợp có n phần tử có số tập con có chẵn phần tử = số tập con có lẻ phần tử.

Giải bài 2.9 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Sử dụng tam giác Pascal, viết khai triển:

a) \({(x – 1)^5}\)

b) \({(2x – 3y)^4}\)

Tam giác Pascal

Lời giải chi tiết

a)

\(\begin{array}{l}{(x – 1)^5} = {x^5} + 5.{x^4}.( – 1) + 10.{x^3}.{( – 1)^2} + 10.{x^2}.{( – 1)^3} + 5x.{( – 1)^4} + {( – 1)^5}\\ = {x^5} – 5{x^4} + 10{x^3} + 10{x^2} + 5x – 1\end{array}\)

b)

\(\begin{array}{l}{(2x – 3y)^4} = {\left( {2x} \right)^4} + 4{\left( {2x} \right)^3}.( – 3y) + 6{\left( {2x} \right)^2}.{( – 3y)^2} + 4\left( {2x} \right).{( – 3y)^3} + {( – 3y)^4}\\ = 16{x^4} – 96{x^3}y + 216{x^2}{y^2} – 216x{y^3} + 81{y^4}\end{array}\)

Giải bài 2.10 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Viết khai triển theo Nhị Thức Newton:

a) \({(x + y)^6}\)

b) \({(1 – 2x)^5}\)

\({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Lời giải chi tiết

a)

\(\begin{array}{l}{(x + y)^6} = C_6^0{x^6} + C_6^1{x^5}.y + C_6^2{x^4}.{y^2} + C_6^3{x^3}.{y^3} + C_6^4{x^2}.{y^4} + C_6^5x.{y^5} + C_6^6{y^6}\\ = {x^6} + 6{x^5}y + 15{x^4}{y^2} + 20{x^3}{y^3} + 15{x^2}{y^4} + 6x{y^5} + {y^6}\end{array}\)

b)

\(\begin{array}{l}{(1 – 2x)^5} = C_5^0{.1^5} + C_5^1{.1^4}.( – 2x) + C_5^2{.1^3}.{( – 2x)^2} + C_5^3{.1^2}.{( – 2x)^3} + C_5^4.1.{( – 2x)^4} + C_5^5{( – 2x)^5}\\ = 1 – 10x + 40{x^2} – 80{x^3} + 80{x^4} – 32{x^5}\end{array}\)

Giải bài 2.11 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Tìm hệ số của \({x^8}\) trong khai triển của \({\left( {2x + 3} \right)^{10}}\)

Số hạng chứa \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{(ax)^k}{b^{n – k}}\)

Do đó hệ số của \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{a^k}{b^{n – k}}\)

Lời giải chi tiết

Số hạng chứa \({x^k}\) trong khai triển của \({\left( {2x + 3} \right)^{10}}\) là \(C_{10}^{10 – k}{(2x)^k}{3^{10 – k}}\)

Số hạng chứa \({x^8}\) ứng với \(k = 8\), tức là số hạng \(C_{10}^2{(2x)^8}{3^2}\) hay \(103680{x^8}\)

Vậy hệ số của \({x^8}\) trong khai triển của \({\left( {2x + 3} \right)^{10}}\) là \(103680.\)

Giải bài 2.12 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Biết hệ số của \({x^2}\) trong khai triển của \({(1 – 3x)^n}\) là 90. Tìm n.

Số hạng chứa \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{(ax)^k}{b^{n – k}}\)

Do đó hệ số của \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{a^k}{b^{n – k}}\)

Lời giải chi tiết

Số hạng chứa \({x^k}\) trong khai triển của \({(1 – 3x)^n}\) hay \({( – 3x + 1)^n}\) là \(C_n^{n – k}{( – 3x)^k}{1^{n – k}}\)

Số hạng chứa \({x^2}\) ứng với \(k = 2\), tức là số hạng \(C_n^{n – 2}{( – 3x)^2}\) hay \(9.C_n^{n – 2}\)

Do đó \(9.C_n^{n – 2} = 90 \Leftrightarrow C_n^{n – 2} = 10 \Leftrightarrow \frac{{n!}}{{\left( {n – 2} \right)!(n – (n – 2))!}} = 10\)

 \(\begin{array}{l} \Leftrightarrow \frac{{n!}}{{\left( {n – 2} \right)!2!}} = 10 \Leftrightarrow \frac{{n(n – 1)}}{2} = 10\\ \Leftrightarrow {n^2} – n – 20 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n =  – 4\;(L)\end{array} \right.\end{array}\)

Vậy \(n = 5\) thì hệ số của \({x^2}\) trong khai triển của \({(1 – 3x)^n}\) là 90.

Giải bài 2.13 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Từ khai triển biểu thức \({(3x – 5)^4}\) thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.

Tam giác Pascal

Lời giải chi tiết

\(\begin{array}{l}{(3x – 5)^4} = {(3x)^4} + 4.{(3x)^3}.( – 5) + 6.{(3x)^2}.{( – 5)^2} + 4.3x.{( – 5)^3} + {( – 5)^4}\\ = 81{x^4} – 540{x^3} + 1350{x^2} – 1500x + 625\end{array}\)

Tổng các hệ số của đa thức là: \(81 – 540 + 1350 – 1500 + 625 = 16\)

Giải bài 2.14 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Tìm hệ số của \({x^5}\) trong khai triển thành đa thức của biểu thức

 \(x{\left( {1 – 2x} \right)^5} + {x^2}{(1 + 3x)^{10}}\)

Tìm hệ số a của \({x^4}\) trong khai triển thành đa thức của \({\left( {1 – 2x} \right)^5}\)

Tìm hệ số a’ của \({x^3}\) trong khai triển thành đa thức của \({(1 + 3x)^{10}}\)

=> Hệ số của \({x^5}\) trong khai triển thành đa thức của biểu thức đã cho là a + a’.

Lời giải chi tiết

+) Tìm hệ số của \({x^4}\) trong khai triển thành đa thức của \({\left( {1 – 2x} \right)^5}\)

Số hạng chứa \({x^k}\) trong khai triển của \({\left( {1 – 2x} \right)^5}\) hay \({\left( { – 2x + 1} \right)^5}\) là \(C_5^{5 – k}{( – 2x)^k}{1^{5 – k}}\)

Số hạng chứa \({x^4}\) ứng với \(k = 4\), tức là số hạng \(C_5^1{( – 2x)^4}\) hay \(80{x^4}\)

Vậy hệ số của \({x^4}\) trong khai triển của \({\left( {1 – 2x} \right)^5}\) là \(80.\)

+) Tìm hệ số của \({x^3}\) trong khai triển thành đa thức của \({(1 + 3x)^{10}}\)

Số hạng chứa \({x^k}\) trong khai triển của \({(1 + 3x)^{10}}\) hay \({(3x + 1)^{10}}\) là \(C_{10}^{10 – k}{(3x)^k}{1^{10 – k}}\)

Số hạng chứa \({x^3}\) ứng với \(k = 3\), tức là số hạng \(C_{10}^7{(3x)^3}\) hay \(3240{x^3}\)

Vậy hệ số của \({x^3}\) trong khai triển của \({(1 + 3x)^{10}}\) là \(3240.\)

=> Hệ số của \({x^5}\) trong khai triển thành đa thức của biểu thức đã cho là 3320.

Giải bài 2.15 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Tính tổng sau đây:

\(C_{2021}^0 – 2C_{2021}^1 + {2^2}C_{2021}^2 – {2^3}C_{2021}^3 + … – {2^{2021}}C_{2021}^{2021}\)

Lời giải chi tiết

Ta có:

\(\begin{array}{l}{(x – 2)^{2021}} = C_{2021}^0{x^{2021}} + C_{2021}^1{x^{2020}}( – 2) + C_{2021}^2{x^{2019}}{( – 2)^2} + C_{2021}^3{x^{2018}}{( – 2)^3} + … + C_{2021}^{2021}{( – 2)^{2021}}\\ = C_{2021}^0{x^{2021}} – 2C_{2021}^1{x^{2020}} + {2^2}C_{2021}^2{x^{2019}} – {2^3}C_{2021}^3{x^{2018}} + … – {2^{2021}}C_{2021}^{2021}\end{array}\)

Thay \(x = 1\) vào cả hai vế, ta suy ra

\(C_{2021}^0 – 2C_{2021}^1 + {2^2}C_{2021}^2 – {2^3}C_{2021}^3 + … – {2^{2021}}C_{2021}^{2021} = {( – 1)^{2021}} =  – 1\)

Giải bài 2.16 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Tìm số tự nhiên n thỏa mãn

\(C_{2n}^0 + C_{2n}^2 + C_{2n}^4… + C_{2n}^{2n} = {2^{2021}}\)

Lời giải chi tiết

\({(1 + x)^{2n}} = C_{2n}^0 + C_{2n}^1x + C_{2n}^2{x^2} + … + C_{2n}^{2n}{x^{2n}}\)

Thay \(x = 1\) vào hai vế, ta suy ra

\(C_{2n}^0 + C_{2n}^1 + C_{2n}^2 + … + C_{2n}^{2n} = {2^{2n}}\)

Thay \(x =  – 1\) vào hai vế, ta suy ra

\(C_{2n}^0 – C_{2n}^1 + C_{2n}^2 – … + C_{2n}^{2n} = 0\)

\(\begin{array}{l} \Rightarrow \left( {C_{2n}^0 + C_{2n}^1 + C_{2n}^2 + … + C_{2n}^{2n}} \right) + \left( {C_{2n}^0 – C_{2n}^1 + C_{2n}^2 – … + C_{2n}^{2n}} \right) = {2^{2n}}\\ \Leftrightarrow 2\left( {C_{2n}^0 + C_{2n}^1 + C_{2n}^2 + … + C_{2n}^{2n}} \right) = {2^{2n}}\\ \Leftrightarrow C_{2n}^0 + C_{2n}^1 + C_{2n}^2 + … + C_{2n}^{2n} = {2^{2n – 1}}\\ \Leftrightarrow 2n – 1 = 2021\\ \Leftrightarrow n = 1011\end{array}\)

Giải bài 2.17 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Tìm số nguyên dương n sao cho

\(C_n^0 + 2C_n^1 + 4C_n^2… + {2^n}C_n^n = 243\)

Lời giải chi tiết

Ta có:

\({(1 + x)^n} = C_n^0 + C_n^1x + C_n^2{x^2} + … + C_n^n{x^n}\)

Thay \(x = 2\) vào hai vế, ta suy ra

\(\begin{array}{l}C_n^0 + 2C_n^1 + {2^2}C_n^2 + … + {2^n}C_n^n = {3^n}\\ \Rightarrow {3^n} = 243 = {3^5}\\ \Leftrightarrow n = 5\end{array}\)

Giải bài 2.18 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức

Đề bài

Biết rằng \({(2 + x)^{100}} = {a_0} + {a_1}x + {a_2}{x^2} + … + {a_{100}}{x^{100}}\). Với giá trị nào của k \((0 \le k \le 100)\) thì \({a_k}\) lớn nhất?

Lời giải chi tiết

Ta có:

\(\begin{array}{l}{(2 + x)^{100}} = C_{100}^0{2^{100}} + C_{100}^1{2^{99}}x + C_{100}^2{2^{98}}{x^2} + … + C_{100}^{100}{x^{100}}\\ \Rightarrow {a_k} = {2^{100 – k}}C_{100}^k\end{array}\)

Để \({a_k}\) lớn nhất thì \({a_{k – 1}} \le {a_k} \ge {a_{k + 1}}\forall k\)

\(\begin{array}{l} \Leftrightarrow {2^{101 – k}}C_{100}^{k – 1} \le {2^{100 – k}}C_{100}^k \ge {2^{99 – k}}C_{100}^{k + 1}\\ \Leftrightarrow {2^{101 – k}}\frac{{100!}}{{(k – 1)!\left( {101 – k} \right)!}} \le {2^{100 – k}}\frac{{100!}}{{k!\left( {100 – k} \right)!}} \ge {2^{99 – k}}\frac{{100!}}{{(k + 1)!\left( {99 – k} \right)!}}\\ \Leftrightarrow {2^2}\frac{1}{{\left( {101 – k} \right)(100 – k)}} \le 2.\frac{1}{{k\left( {100 – k} \right)}} \ge \frac{1}{{k(k + 1)}}\\ \Leftrightarrow \left\{ \begin{array}{l}\frac{4}{{\left( {101 – k} \right)(100 – k)}} \le \frac{2}{{k\left( {100 – k} \right)}}\\\frac{2}{{k\left( {100 – k} \right)}} \ge \frac{1}{{k(k + 1)}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\frac{2}{{101 – k}} \le \frac{1}{k}\\\frac{2}{{100 – k}} \ge \frac{1}{{k + 1}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2k \le 101 – k\\2(k + 1) \ge 100 – k\end{array} \right.\\ \Leftrightarrow \frac{{98}}{3} \le k \le \frac{{101}}{3} \Rightarrow k = 33\;(k \in \mathbb{N})\end{array}\)

Vậy \({a_{33}}\) là lớn nhất.