Giải Bài 3. Parabol – Chuyên đề Toán 10 (Chân trời)
===========
Giải mục 1 trang 56, 57, 58 Chuyên đề học tập Toán 10
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1
Chứng tỏ rằng nếu điểm \(M({x_0};{y_0})\) nằm trên parabol (P) thì điểm \(N({x_0}; – {y_0})\) cũng nằm trên parabol (P)

Lời giải chi tiết:
Nếu điểm \(M({x_0};{y_0})\) nằm trên parabol thì \({y_0}^2 = 2p{x_0} \Leftrightarrow {( – {y_0})^2} = 2p{x_0}\)
nên điểm \(M'({x_0}; – {y_0})\) cũng nằm trên parabol.
Thực hành 1
Tìm tọa độ tiêu điểm, tọa độ đỉnh, phương trình đường chuẩn và trục đối xứng của các parabol sau:
a) \(({P_1}):{y^2} = 2x\)
b) \(({P_2}):{y^2} = x\)
c) \(({P_3}):{y^2} = \frac{1}{5}x\)
Phương pháp giải:
Cho parabol có PTCT \({y^2} = 2px\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đỉnh O(0;0)
+ Đường chuẩn: \(\Delta : x = – \frac{p}{2}\)
+ Trục đối xứng: Ox
Lời giải chi tiết:
a) Ta có: \(2p = 2\), suy ra \(p = 1\).
Vậy \(({P_1})\) có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta : x = – \frac{1}{2}\) và nhận Ox làm trục đối xứng.
b) Ta có: \(2p = 1\), suy ra \(p = \frac{1}{2}\).
Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta : x = – \frac{1}{4}\) và nhận Ox làm trục đối xứng.
c) Ta có: \(2p = \frac{1}{5}\), suy ra \(p = \frac{1}{{10}}\).
Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{{20}};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta : x = – \frac{1}{{20}}\) và nhận Ox làm trục đối xứng.
Vận dụng 1
Trong mặt phẳng Oxy, cho điểm \(A(2;0)\) và đường thẳng \(d: x + 2 = 0\). Viết phương trình của đường (L) là tập hợp các tâm \(J(x;y)\) của các đường tròn (C) thay đổi nhưng luôn luôn đi qua A và tiếp xúc với d.
Lời giải chi tiết:
Ta có: (C) đi qua \(A(2;0)\) và tiếp xúc với \(d: x + 2 = 0\)
\(\begin{array}{l} \Rightarrow d(J,d) = JA\\ \Leftrightarrow \left| {x + 2} \right| = \sqrt {{{(x – 2)}^2} + {y^2}} \\ \Leftrightarrow {\left( {x + 2} \right)^2} = {(x – 2)^2} + {y^2}\\ \Leftrightarrow {x^2} + 4x + 4 = {x^2} – 4x + 4 + {y^2}\\ \Leftrightarrow {y^2} = 8x\end{array}\)
Tức là tâm \(J(x;y)\) của (C) nằm trên parabol (P) \({y^2} = 8x\)
Giải mục 2 trang 55, 56, 57, 58 Chuyên đề học tập Toán 10
Lựa chọn câu để xem lời giải nhanh hơn
HĐ2
Cho điểm \(M(x;y)\) trên parabol (P) \({y^2} = 2px\) (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm \(F\) của (P).
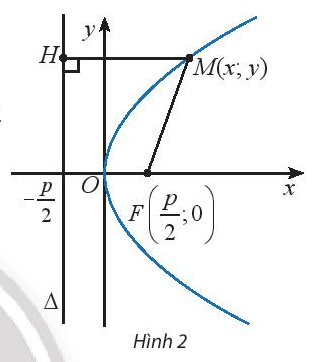
Lời giải chi tiết:
Tiêu điểm \(F(\frac{p}{2};0)\)
Ta có:
\(MF = \sqrt {{{\left( {x – \frac{p}{2}} \right)}^2} + {y^2}} = \sqrt {{{\left( {x – \frac{p}{2}} \right)}^2} + 2p{x_0}} = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}} = x + \frac{p}{2}\);
Thực hành 2
Tính bán kính qua tiêu của điểm dưới đây trên parabol tương ứng.
a) Điểm \({M_1}(1; – 4)\) trên \(({P_1}):{y^2} = 16x\)
b) Điểm \({M_2}(3; – 3)\) trên \(({P_2}):{y^2} = 3x\)
c) Điểm \({M_3}(4;1)\) trên \(({P_3}):{y^2} = \frac{1}{4}x\)
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Với \(M({x_0};{y_0})\) thuộc parabol, bán kính qua tiêu: \(FM = {x_0} + \frac{p}{2}\)
Lời giải chi tiết:
a) \(({P_1}):{y^2} = 16x\)
Ta có \(2p = 16\), suy ra \(p = 8\). Vậy độ dài bán kính qua tiêu của điểm \({M_1}(1; – 4)\) là: \(FM = x + \frac{p}{2} = 1 + \frac{8}{2} = 5.\)
b) \(({P_2}):{y^2} = 3x\)
Ta có \(2p = 3\), suy ra \(p = \frac{3}{2}\). Vậy độ dài bán kính qua tiêu của điểm \({M_2}(3; – 3)\) là: \(FM = x + \frac{p}{2} = 3 + \frac{{\frac{3}{2}}}{2} = \frac{{15}}{4}.\)
c) \(({P_3}):{y^2} = \frac{1}{4}x\)
Ta có \(2p = \frac{1}{4}\), suy ra \(p = \frac{1}{8}\). Vậy độ dài bán kính qua tiêu của điểm \({M_3}(4;1)\) là: \(FM = x + \frac{p}{2} = 4 + \frac{{\frac{1}{8}}}{2} = \frac{{65}}{{16}}.\)
Vận dụng 2
Một cổng có dạng một đường parabol (P). Biết chiều cao của cổng là 7,6 m và khoảng cách giữa hai chân cổng là 9m. Người ta muốn treo một ngôi sao tại tiêu điểm F của (P) bằng một đoạn dây nối từ đỉnh S của cổn. Tính khoảng cách từ tâm ngôi sao đến đỉnh cổng.
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Tiêu điểm \(F(\frac{p}{2};0)\)
Lời giải chi tiết:
Gọi phương trình chính tắc của parabol là: \({y^2} = 2px\)
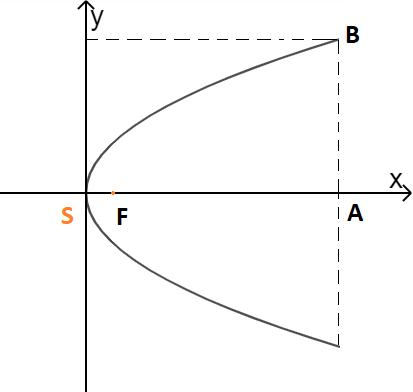
Chiều cao của cổng là 7,6 m nên \(A(7,6;0)\)
Khoản cách giữa hai chân cổng là 9m nên \(B(7,6;4,5)\)
\(B \in (P)\) suy ra \(4,{5^2} = 2p.7,6 \Rightarrow p = \frac{{405}}{{304}}\)
Tiêu điểm F của (P) có tọa độ: \(F\left( {\frac{{405}}{{608}};0} \right)\)
Hay khoảng cách từ tâm ngôi sao đến đỉnh cổng là \(\frac{{405}}{{608}} \approx 0,67(m)\),
Vận dụng 3
Mặt cắt của một chảo ăng-ten có dạng một parabol (P) có phương trình chính tắc \({y^2} = 0,25x\). Biết đầu thu tín hiệu của chảo ăng-ten tại tiêu điểm F của (P). Tính khoảng cách từ điểm \(M(0,25;0,25)\) trên ăng-ten đến F.
Phương pháp giải:
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
+) Tiêu điểm \(F(\frac{p}{2};0)\)
Lời giải chi tiết:
(P) \({y^2} = 0,25x\) có \(2p = 0,25 \Leftrightarrow p = \frac{1}{8}\)
Khoảng cách từ điểm \(M(0,25;0,25)\) trên ăng-ten đến \(F\) là:
\(MF = {x_M} + \frac{p}{2} = 0,25 + \frac{{\frac{1}{8}}}{2} = 0,3125\)
Giải bài 1 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Đề bài
Tìm tọa độ tiêu điểm và phương trình đường chuẩn của các parabol sau:
a) \(({P_1}):{y^2} = 2x\)
b) \(({P_2}):{y^2} = x\)
c) \(({P_3}):{y^2} = \frac{1}{5}x\)
Cho parabol có PTCT \({y^2} = 2px\)
+ Tiêu điểm: \(F(\frac{p}{2};0)\)
+ Đường chuẩn: \(\Delta : x = – \frac{p}{2}\)
Lời giải chi tiết
a) Ta có: \(2p = 2\), suy ra \(p = 1\).
Vậy \(({P_1})\) có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\), đường chuẩn \(\Delta : x = – \frac{1}{2}\).
b) Ta có: \(2p = \frac{1}{3}\), suy ra \(p = \frac{1}{6}\).
Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{{12}};0} \right)\), đường chuẩn \(\Delta : x = – \frac{1}{{12}}\).
c) Ta có: \(2p = \sqrt 2 \), suy ra \(p = \frac{{\sqrt 2 }}{2}\).
Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{{\sqrt 2 }}{4};0} \right)\), đường chuẩn \(\Delta : x = – \frac{{\sqrt 2 }}{4}\).
Giải bài 2 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Đề bài
Tìm bán kính qua tiêu của điểm đã cho trên các parabol sau:
a) Điểm \({M_1}(3; – 6)\) trên \(({P_1}):{y^2} = 12x\)
b) Điểm \({M_2}(6;1)\) trên \(({P_2}):{y^2} = \frac{1}{6}x\)
c) Điểm \({M_3}(\sqrt 3 ;\sqrt 3 )\) trên \(({P_3}):{y^2} = \sqrt 3 x\)
Cho parabol có phương trình chính tắc \({y^2} = 2px\)
Với \(M({x_0};{y_0})\) thuộc parabol, bán kính qua tiêu: \(FM = {x_0} + \frac{p}{2}\)
Lời giải chi tiết
a) \(({P_1}):{y^2} = 12x\)
Ta có \(2p = 12\), suy ra \(p = 6\). Vậy độ dài bán kính qua tiêu của điểm \({M_1}(3; – 6)\) là: \(FM = x + \frac{p}{2} = 3 + \frac{6}{2} = 6.\)
b) \(({P_2}):{y^2} = \frac{1}{6}x\)
Ta có \(2p = \frac{1}{6}\), suy ra \(p = \frac{1}{{12}}\). Vậy độ dài bán kính qua tiêu của điểm \({M_2}(6;1)\) là: \(FM = x + \frac{p}{2} = 6 + \frac{{\frac{1}{{12}}}}{2} = \frac{{145}}{{24}}.\)
c) \(({P_3}):{y^2} = \sqrt 3 x\)
Ta có \(2p = \sqrt 3 \), suy ra \(p = \frac{{\sqrt 3 }}{2}\). Vậy độ dài bán kính qua tiêu của điểm \({M_3}(\sqrt 3 ;\sqrt 3 )\) là: \(FM = x + \frac{p}{2} = \sqrt 3 + \frac{{\frac{{\sqrt 3 }}{2}}}{2} = \frac{{5\sqrt 3 }}{4}.\)
Giải bài 3 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Đề bài
Trong mặt phẳng Oxy, cho điểm \(A(\frac{1}{4};0)\) và đường thẳng \(d: x + \frac{1}{4} = 0\). Viết phương trình của đường (P) là tập hợp các tâm \(M(x;y)\) của các đường tròn (C) thay đổi nhưng luôn luôn đi qua A và tiếp xúc với d.
Lời giải chi tiết
Ta có: (C) đi qua \(A(\frac{1}{4};0)\) và tiếp xúc với \(d: x + \frac{1}{4} = 0\)
\(\begin{array}{l} \Rightarrow d(M,d) = MA\\ \Leftrightarrow \left| {x + \frac{1}{4}} \right| = \sqrt {{{\left( {x – \frac{1}{4}} \right)}^2} + {y^2}} \\ \Leftrightarrow {\left( {x + \frac{1}{4}} \right)^2} = {\left( {x – \frac{1}{4}} \right)^2} + {y^2}\\ \Leftrightarrow {y^2} = x\end{array}\)
Tức là tâm \(M(x;y)\) của (C) nằm trên parabol (P) \({y^2} = x\)
Giải bài 4 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Đề bài
Cho parabol (P). Trên (P) lấy hai điểm M, N sao cho đoạn thẳng MN đi qua tiêu điểm F của (P). Chứng minh rằng khoảng cách từ trung điểm I của đoạn thẳng MN đến đường chuẩn của (P) bằng \(\frac{1}{2}MN\) và đường tròn đường kính MN tiếp xúc với \(\Delta \).
Với điểm M bất kì nằm trên parabol ta có: \(d(M,\Delta ) = MF\)
Lời giải chi tiết
Gọi PTCT của parabol là \({y^2} = 2px\)
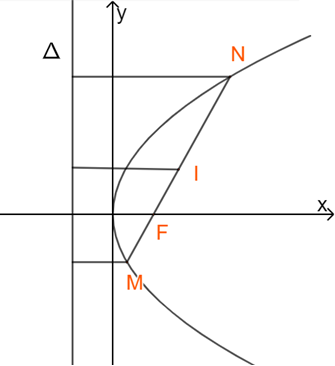
M, N nằm trên parabol nên ta có: \(d(M,\Delta ) = MF;d(N,\Delta ) = NF\)
\( \Rightarrow d\left( {I,\Delta } \right) = \frac{{d(M,\Delta ) + d(N,\Delta )}}{2} = \frac{{MF + NF}}{2} = \frac{{MN}}{2}\)
Giải bài 5 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Đề bài
Hãy so sánh bán kính qua tiêu của điểm M trên parabol (P) với bán kính của đường tròn tâm M, tiếp xúc với đường chuẩn của (P).
Lời giải chi tiết
Gọi PTCT của parabol là \({y^2} = 2px\)
Có phương trình đường chuẩn là \(\Delta : x = – \frac{p}{2}\)
Giả sử \(M(x;y)\) nằm trên parabol, ta có: \(d(M,\Delta ) = MF\)
Vì \(MF = \sqrt {{{\left( {x – \frac{p}{2}} \right)}^2} + {y^2}} = \sqrt {{{\left( {x – \frac{p}{2}} \right)}^2} + 2px} = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}} = \left| {x + \frac{p}{2}} \right| = d(M,\Delta )\)
Hay \(MF = d(M,\Delta ) = R\) là bán kính của đường tròn tâm M và tiếp xúc với \(\Delta \).
Giải bài 6 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Đề bài
Một sao chổi A chuyển động theo quỹ đạo có dạng một parabol (P) nhận tâm Mặt Trời là tiêu điểm. Cho biết khoảng cách ngắn nhất giữa sao chổi A và tâm Mặt Trời là khoảng 112 km.
a) Viết phương trình chính tắc của parabol (P)
b) Tính khoảng cách giữa sao chổi A và tâm Mặt Trời khi sao chổi nằm trên đường thẳng đi qua tiêu điểm và vuông góc với trục đối xứng của (P).
Cho parabol \({y^2} = 2px\)
Tiêu điểm \(F\left( {\frac{p}{2};0} \right)\)
Khoảng cách ngắn nhất của \(MF\) là \(MF = \frac{p}{2}\), xảy ra ra khi M là đỉnh của parabol.
Lời giải chi tiết
a) Gọi PTCT của parabol là \({y^2} = 2px\)
Với \(M(x;y)\) bất kì nằm trên parabol, ta có: \(MF = x + \frac{p}{2} \ge \frac{p}{2}\) (do \(x \ge 0\))
Vì khoảng cách ngắn nhất giữa sao chổi A và tâm Mặt Trời là khoảng 112 km nên \(\frac{p}{2} = 112 \Leftrightarrow p = 224\)
\( \Rightarrow \) Phương trình chính tắc của (P) là: \({y^2} = 448x\)
b)
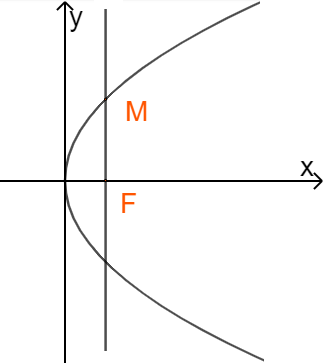
Gọi \(M(x;y)\) là vị trí sao chổi A, nằm trên đường thẳng đi qua tiêu điểm và vuông góc với trục đối xứng của (P).
Parabol (P) có tiêu điểm \(F(112;0)\) \( \Rightarrow M(112;y)\)
\(MF = \left| {{y_M}} \right| = \sqrt {2.224.112} = 224\)
Vậy khoảng cách là 224 km.
Giải bài 7 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Đề bài
Mặt cắt của gương phản chiếu của một đèn pha có dạng một parabol (P) có phương trình chính tắc \({y^2} = 6x\). Tính khoảng cách từ điểm \(M(1;\sqrt 6 )\) trên gương đến tiêu điểm của (P). (với đơn vị trên hệ trục tọa độ là xentimet)
Cho parabol \({y^2} = 2px\), \(M({x_0};{y_0})\) thuộc parabol, bán kính qua tiêu: \(FM = {x_0} + \frac{p}{2}\)
Lời giải chi tiết
Ta có: \(2p = 6 \Leftrightarrow p = 3\)
\(M(1;\sqrt 6 )\) nằm trên parabol vì \({\left( {\sqrt 6 } \right)^2} = 6.1\)
Bán kính qua tiêu: \(MF = x + \frac{p}{2} = 1 + \frac{3}{2} = 2,5\) (cm)
