
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy, \(SA = a\sqrt 2\). Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD.
- A. \(V = \frac{{32}}{3}\pi {a^3}\).
- B. \(V = \frac{{4}}{3}\pi {a^3}\).
- C. \(V =4\pi {a^3}\).
- D. \(V = \frac{{4\sqrt 2 }}{3}\pi {a^3}\).
Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Đáp án đúng: B
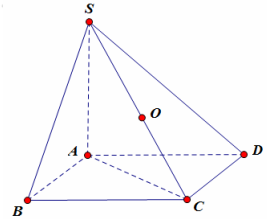
Dễ thấy SAC, SAC, SDC là các tam giác vuông nhận SC làm cạnh huyền, nên tâm mặt cầu ngoại tiếp khối chóp S.ABCD là trung điểm của SC.
Bán kính khối cầu ngoại tiếp hình chóp SABCD là: \(R = \frac{{SC}}{2} = \frac{{\sqrt {S{A^2} + A{C^2}} }}{2} = a.\)
Thể tích khối cầu \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {a^3}\).
=======
Xem thêm Lý thuyết khối tròn xoay
