Cắt hình trụ bởi mặt phẳng (\(\alpha \)) vuông góc với mặt đáy, ta được thiết diện là hình vuông có diện tích bằng 16. Khoảng cách từ tâm đường tròn đáy của hình trụ đến mặt phẳng (\(\alpha \)) bằng 3. Thể tích khối trụ bằng:

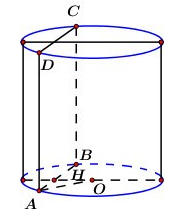
Ta có ABCD là hình vuông \(
\Rightarrow {S_{ABCD}} = A{B^2} = 16 \Rightarrow AB = AD = 4\)

Gọi H là trung điểm của AB⇒OH⊥AB

Lại có: (ABCD) vuông góc với mặt phẳng đáy ⇒OH⊥AD

\(
\Rightarrow OH \bot \left( {ABCD} \right) \Rightarrow d\left( {O;{\mkern 1mu} {\mkern 1mu} \left( {ABCD} \right)} \right) = OH = 3\)

Áp dụng định lý Pitago cho ΔOAH vuông tại H ta có:

\(
OA = \sqrt {O{H^2} + {{\left( {\frac{{AB}}{2}} \right)}^2}} = \sqrt {{3^2} + {2^2}} = \sqrt {13} \)

Khi đó ta có thể tích của hình trụ đã cho là:

\(
V = \pi {R^2}h = \pi .O{A^2}.AD = \pi .13.4 = 52\pi .\)