Câu hỏi:
Cho hình trụ có bán kính đáy bằng R và chiều cao bằng \(3R\over 2\) . Mặt phẳng \((\alpha)\)song song với trục của hình trụ và cách trục một khoảng bằng \(R\over 2\). Diện tích thiết diện của hình trụ với mp (α ) là:
Lời Giải:
Đây là các bài toán tính toán S, V về Mặt trụ, Hình trụ, Khối trụ trong Phần Mặt tròn xoay.
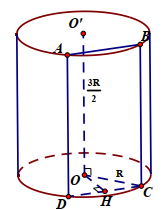
Theo đề bài ta có:
\(\begin{array}{l}
h = \frac{{3R}}{2};OH = \frac{R}{2}\\
\Rightarrow HC = \sqrt {O{C^2} – O{H^2}} = \sqrt {{R^2} – {{\left( {\frac{R}{2}} \right)}^2}} = \frac{{{R^2}\sqrt 3 }}{2}\\
Vậy\,\,{S_{ABCD}} = DC.AB = 2HC.AD = 2.\frac{{{R^2}\sqrt 3 }}{2}.\frac{{3R}}{2} = \frac{{3{R^2}\sqrt 3 }}{2}
\end{array}\)
===============
====================
Thuộc chủ đề: Trắc nghiệm Mặt Trụ
