Cho lăng trụ \(ABCD.EFGH\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(\widehat {ABD} = 60^\circ \). Góc giữa mặt phẳng \(\left( {EBD} \right)\) và mặt đáy bằng \(60^\circ \). Đỉnh \(E\) cách đều các điểm \(A\), \(B\), \(D\). Tính theo \(a\) thể tích \(V\) của khối lăng trụ đã cho. A. \(V = \frac{{{a^3}\sqrt 3 }}{2}\). B. \(V = \frac{{{a^3}\sqrt 3 }}{6}\). C. \(V = … [Đọc thêm...] vềCho lăng trụ \(ABCD.EFGH\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(\widehat {ABD} = 60^\circ \). Góc giữa mặt phẳng \(\left( {EBD} \right)\) và mặt đáy bằng \(60^\circ \). Đỉnh \(E\) cách đều các điểm \(A\), \(B\), \(D\). Tính theo \(a\) thể tích \(V\) của khối lăng trụ đã cho.
Cho lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều cạnh \(a\). Hình chiếu vuông góc của điểm \(A’\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA’\) và \(BC\) bằng \(\frac{{a\sqrt 3 }}{4}\). Khi đó thể tích của khối lăng trụ là
Cho lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Hình chiếu vuông góc của điểm \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA'\) và \(BC\) bằng \(\frac{{a\sqrt 3 }}{4}\). Khi đó thể tích của khối lăng trụ là A. \(\frac{{{a^3}\sqrt 3 }}{{12}}.\) B. \(\frac{{{a^3}\sqrt 3 … [Đọc thêm...] vềCho lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều cạnh \(a\). Hình chiếu vuông góc của điểm \(A’\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA’\) và \(BC\) bằng \(\frac{{a\sqrt 3 }}{4}\). Khi đó thể tích của khối lăng trụ là
Đề thi thử TN THPT môn Toán năm 2024 – SỞ CẦN THƠ -.docx
Đề thi thử TN THPT môn Toán năm 2024 - SỞ CẦN THƠ -.docx ========== booktoan.com chia sẻ đến các ĐỀ THI TN THPT MÔN TOÁN 2024. Đề THI có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong kỳ thi TN THPT năm nay, ĐỖ NGUYỆN VỌNG 1. NGUỒN: BOOKTOAN.COM sưu tập trên internet.... ———– xem file de thi … [Đọc thêm...] vềĐề thi thử TN THPT môn Toán năm 2024 – SỞ CẦN THƠ -.docx
Đề thi thử TN THPT Toán 2024 – SỞ KON TUM -.docx
Đề thi thử TN THPT Toán 2024 – SỞ KON TUM -.docx ========== booktoan.com chia sẻ đến các ĐỀ THI TN THPT MÔN TOÁN 2024. Đề THI có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong kỳ thi TN THPT năm nay, ĐỖ NGUYỆN VỌNG 1. NGUỒN: BOOKTOAN.COM sưu tập trên internet.... ———– xem file de thi … [Đọc thêm...] vềĐề thi thử TN THPT Toán 2024 – SỞ KON TUM -.docx
Đề thi thử TN THPT Toán 2024 – KIM LIÊN – HÀ NỘI – LẦN 3 -.docx
Đề thi thử TN THPT Toán 2024 – KIM LIÊN - HÀ NỘI – LẦN 3 -.docx ========== booktoan.com chia sẻ đến các ĐỀ THI TN THPT MÔN TOÁN 2024. Đề THI có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong kỳ thi TN THPT năm nay, ĐỖ NGUYỆN VỌNG 1. NGUỒN: BOOKTOAN.COM sưu tập trên internet.... ———– xem file … [Đọc thêm...] vềĐề thi thử TN THPT Toán 2024 – KIM LIÊN – HÀ NỘI – LẦN 3 -.docx
Đề thi thử TN THPT TOÁN 2024 – SỞ GD NINH BÌNH LẦN 3.docx
Đề thi thử TN THPT TOÁN 2024 - SỞ GD NINH BÌNH LẦN 3.docx ========== booktoan.com chia sẻ đến các ĐỀ THI TN THPT MÔN TOÁN 2024. Đề THI có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong kỳ thi TN THPT năm nay, ĐỖ NGUYỆN VỌNG 1. NGUỒN: BOOKTOAN.COM sưu tập trên internet.... ———– xem file de … [Đọc thêm...] vềĐề thi thử TN THPT TOÁN 2024 – SỞ GD NINH BÌNH LẦN 3.docx
Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.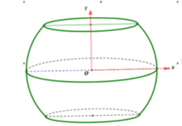
Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.
A. \(\frac{{100}}{3}\pi \left( {d{m^3}} \right)\).
B. \(\frac{{43}}{3}\pi \left( … [Đọc thêm...] về Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( x \right) + f\left( x \right) = x,\)\(\forall x \in \mathbb{R}.\)Tính \(\int\limits_0^2 {f\left( x \right)} dx.\)
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( x \right) + f\left( x \right) = x,\)\(\forall x \in \mathbb{R}.\)Tính \(\int\limits_0^2 {f\left( x \right)} dx.\) A. \(\frac{5}{4}\). B. \(\frac{3}{2}\). C. \(\frac{1}{2}\). D. \(2\). Lời giải Đặt: \(y = f\left( x \right) \Rightarrow x = {y^3} + y.\) \( \Rightarrow dx = … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( x \right) + f\left( x \right) = x,\)\(\forall x \in \mathbb{R}.\)Tính \(\int\limits_0^2 {f\left( x \right)} dx.\)
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(2f\left( x \right) – f’\left( x \right) = 3x\left( {2x – 5} \right)\), \(\forall x \in \mathbb{R}\). Biết rằng \(f\left( 0 \right) = – 1\). Giá trị của \(f\left( 2 \right)\) bằng
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(2f\left( x \right) - f'\left( x \right) = 3x\left( {2x - 5} \right)\), \(\forall x \in \mathbb{R}\). Biết rằng \(f\left( 0 \right) = - 1\). Giá trị của \(f\left( 2 \right)\) bằng A. \(7\). B. \(6\). C. \(1\). D. \(2\). Lời giải Ta có: \(2f\left( x \right) - f'\left( x … [Đọc thêm...] về Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(2f\left( x \right) – f’\left( x \right) = 3x\left( {2x – 5} \right)\), \(\forall x \in \mathbb{R}\). Biết rằng \(f\left( 0 \right) = – 1\). Giá trị của \(f\left( 2 \right)\) bằng
Cho hàm số \(f(x)\) liên tục với mọi \(x \ne 0\) thỏa mãn:\(f(x) + 2f\left( {\frac{1}{x}} \right) = 3x\) với \(x \ne 0\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), và hai đường thẳng \(x = 1;\,x = 2\).
Cho hàm số \(f(x)\) liên tục với mọi \(x \ne 0\) thỏa mãn:\(f(x) + 2f\left( {\frac{1}{x}} \right) = 3x\) với \(x \ne 0\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), và hai đường thẳng \(x = 1;\,x = 2\). A. \(\frac{{{\pi ^2}}}{{12}}\). B. \(\frac{\pi }{3}\). C. \(\frac{\pi … [Đọc thêm...] về Cho hàm số \(f(x)\) liên tục với mọi \(x \ne 0\) thỏa mãn:\(f(x) + 2f\left( {\frac{1}{x}} \right) = 3x\) với \(x \ne 0\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), và hai đường thẳng \(x = 1;\,x = 2\).
