Giải Bài 4. Tính chất chung của ba đường conic – Chuyên đề Toán 10 (Chân trời)

Giải Bài 4. Tính chất chung của ba đường conic – Chuyên đề Toán 10 (Chân trời)

============

Giải mục 1 trang 60, 61 Chuyên đề học tập Toán 10

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Gắn một đoạn ống nhựa vào đầu bóng của một đèn chiếu nhỏ để tạo ra một chùm ánh sáng hình mặt nón tròn xoay (Hình 1a, b). Chiếu đèn lên một bức tường với các góp nghiêng khác nhau để ánh sáng từ đèn hắt lên bức tường tạo thành các bóng khác nhau (HÌnh 1c, d, e). Nhận xét hình ảnh bạn nhìn thấy trên bức tường.

Lời giải chi tiết:

Hình 1c: Hình ảnh trên bức tường là hình elip

Hình 1d: Hình ảnh trên bức tường là hypebol

Hình 1e: Hình ảnh trên bức tường là parabol

Thực hành 1

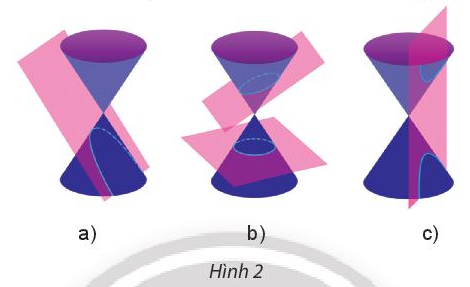
Giao của mặt phẳng và mặt nón trong Hình 2b, c có dạng đường gì?

Lời giải chi tiết:

Trong Hình 2b, giao của mặt phẳng và mặt nón là một elip hoặc một đường tròn.

Trong Hình 2c, giao của mặt phẳng và mặt nón là một hypebol.

Vận dụng 1

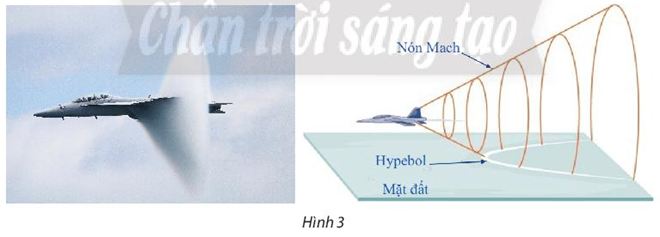
Khi máy bay bay song song với mặt đất với vận tốc lớn hơn vận tốc của âm thanh sẽ tạo ra các lớp không khí dao động có hình mặt nón (nón Mach) (Hình 3) và tạo ra tiếng nổ mạnh, gọi là tiếng nổ siêu thanh. Những người trên mặt đất nếu nghe thấy tiếng nổ này cùng một thời điểm thì vị trí của họ cùng thuộc một đường hypebol. Hãy giải thích.

Lời giải chi tiết:

Những người trên mặt đất nếu nghe thấy tiếng nổ này cùng một thời điểm thì vị trí của họ thuộc giao của nón Mach với mặt đất.

Quan sát thấy giao tuyến này chính là một nhánh của hypebol.

Giải mục 2 trang 61, 62, 63, 64 Chuyên đề học tập Toán 10

Lựa chọn câu để xem lời giải nhanh hơn

HĐ2

Cho đường conic có tiêu điểm F, đường chuẩn \(\Delta \) và một điểm M là điểm nằm trên đường conic đó. Tìm mối liên hệ giữa tỉ số \(\frac{{MF}}{{d(M,\Delta )}}\) và tên gọi của đường conic đó.

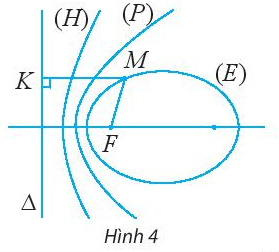
Lời giải chi tiết:

+ Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \(M(x;y) \in (E)\)

\(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{a + ex}}{{\frac{{a + ex}}{e}}} = e\), \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{{a – ex}}{{\frac{{a – ex}}{e}}} = e\)

Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = e = \frac{c}{a} < 1\)

+ Hypebol (H):  \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\), \(M(x;y) \in (H)\)

\(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{\left| {a + ex} \right|}}{{\left| {x + \frac{a}{e}} \right|}} = \frac{{\left| {a + ex} \right|}}{{\frac{{\left| {a + ex} \right|}}{e}}} = e\); \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{\left| {a – ex} \right|}}{{\left| {x – \frac{a}{e}} \right|}} = \frac{{\left| {a – ex} \right|}}{{\frac{{\left| {a – ex} \right|}}{e}}} = e\) ;

Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = e = \frac{c}{a} > 1\)

+ Parabol (P)  \({y^2} = 2px\)

\(\frac{{MF}}{{d(M,\Delta )}} = e = 1\)

Kết luận các đường conic đều có \(\frac{{MF}}{{d(M,\Delta )}} = e\) và

\(\frac{{MF}}{{d(M,\Delta )}} < 1\) thì conic là đường elip

\(\frac{{MF}}{{d(M,\Delta )}} = 1\) thì conic là đường parabol

\(\frac{{MF}}{{d(M,\Delta )}} > 1\) thì conic là đường hypebol

Thực hành 2

Xác định tâm sai, tọa độ tiêu điểm và phương trình đường chuẩn tương ứng của mỗi đường conic sau:

a) \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{2} = 1\)

b) \(\frac{{{x^2}}}{{12}} – \frac{{{y^2}}}{4} = 1\)

c) \({y^2} = \frac{1}{2}x\)

Phương pháp giải:

a) Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \(c = \sqrt {{a^2} – {b^2}} \)

+ Tâm sai của elip: \(e = \frac{c}{a}\)

+ Tiêu điểm \({F_1}( – c;0),{F_2}(c;0)\)

+ Đường chuẩn: \({\Delta _1}: x =  – \frac{a}{e}\) và \({\Delta _2}: x = \frac{a}{e}\).

b) Hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\), \(c = \sqrt {{a^2} + {b^2}} \)

+ Tâm sai của hypebol: \(e = \frac{c}{a}\)

+ Tiêu điểm \({F_1}( – c;0),{F_2}(c;0)\)

+ Đường chuẩn: \({\Delta _1}: x =  – \frac{a}{e}\) và \({\Delta _2}: x = \frac{a}{e}\).

c) Parabol (P)  \({y^2} = 2px\)

+ Tâm sai \(e = 1\)

+ Tiêu điểm \(F(\frac{p}{2};0)\)

+ Đường chuẩn: \(\Delta : x =  – \frac{p}{2}\)

Lời giải chi tiết:

a) Elip (E): \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{2} = 1\), suy ra \(c = \sqrt {{a^2} – {b^2}}  = \sqrt 3 \)

+ Tâm sai của elip: \(e = \frac{c}{a} = \frac{{\sqrt 3 }}{{\sqrt 5 }} = \frac{{\sqrt {15} }}{5}\)

+ Tiêu điểm \({F_1}( – \sqrt 3 ;0),{F_2}(\sqrt 3 ;0)\)

+ Đường chuẩn: \({\Delta _1}: x =  – \frac{{5\sqrt 3 }}{3}\) và \({\Delta _2}: x = \frac{{5\sqrt 3 }}{3}\).

b) Hypebol (H): \(\frac{{{x^2}}}{{12}} – \frac{{{y^2}}}{4} = 1\), \(c = \sqrt {{a^2} + {b^2}}  = 4\)

+ Tâm sai của hypebol: \(e = \frac{c}{a} = \frac{4}{{2\sqrt 3 }} = \frac{{2\sqrt 3 }}{3}\)

+ Tiêu điểm \({F_1}( – 4;0),{F_2}(4;0)\)

+ Đường chuẩn: \({\Delta _1}: x =  – 3\) và \({\Delta _2}: x = 3\).

c) Parabol (P): \({y^2} = \frac{1}{2}x\), suy ra \(p = \frac{1}{4}\)

+ Tâm sai \(e = 1\)

+ Tiêu điểm \(F(\frac{1}{8};0)\)

+ Đường chuẩn: \(\Delta : x =  – \frac{1}{8}\)

Vận dụng 2

Quỹ đạo của các vật thể sau đây là những đường conic. Những đường này là elip, parabol hay hypebol.

 

Tên	Tâm sai
Trái Đất	0,0167
Sao chổi Halley	0,9671
Sao chổi Great Southern of 1887	1,0
Vật thể Oumuamua	1,2

(Nguồn: https://vi.wikipedia.org/wiki/oumuamud)

Phương pháp giải:

Đường conic có tâm sai e:

+ \(0 < e < 1\) thì conic là đường elip

+ \(e = 1\) thì conic là đường parabol

+ \(e > 1\) thì conic là đường hypebol

Lời giải chi tiết:

 

Tên	Tâm sai	So sánh với 0 và 1	Kết luận
Trái Đất	0,0167	0 < 0,0167 < 1	Elip
Sao chổi Halley	0,9671	0 < 0,9671 < 1	Elip
Sao chổi Great Southern of 1887	1,0	1	Parabol
Vật thể Oumuamua	1,2	1,2 > 1	hypebol

Giải bài 1 trang 64 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Xác định tâm sai, tọa độ tiêu điểm và phương trình đường chuẩn tương ứng của mỗi đường conic sau:

a) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\)

b) \(\frac{{{x^2}}}{{15}} – \frac{{{y^2}}}{{10}} = 1\)

c) \({y^2} = x\)

a) Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \(c = \sqrt {{a^2} – {b^2}} \)

+ Tâm sai của elip: \(e = \frac{c}{a}\)

+ Tiêu điểm \({F_1}( – c;0),{F_2}(c;0)\)

+ Đường chuẩn: \({\Delta _1}: x =  – \frac{a}{e}\) và \({\Delta _2}: x = \frac{a}{e}\).

b) Hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\), \(c = \sqrt {{a^2} + {b^2}} \)

+ Tâm sai của hypebol: \(e = \frac{c}{a}\)

+ Tiêu điểm \({F_1}( – c;0),{F_2}(c;0)\)

+ Đường chuẩn: \({\Delta _1}: x =  – \frac{a}{e}\) và \({\Delta _2}: x = \frac{a}{e}\).

c) Parabol (P)  \({y^2} = 2px\)

+ Tâm sai \(e = 1\)

+ Tiêu điểm \(F(\frac{p}{2};0)\)

+ Đường chuẩn: \(\Delta : x =  – \frac{p}{2}\)

Lời giải chi tiết

a) Elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\), suy ra \(c = \sqrt {{a^2} – {b^2}}  = \sqrt 2 \)

+ Tâm sai của elip: \(e = \frac{c}{a} = \frac{{\sqrt 2 }}{3}\)

+ Tiêu điểm \({F_1}( – \sqrt 2 ;0),{F_2}(\sqrt 2 ;0)\)

+ Đường chuẩn: \({\Delta _1}: x =  – \frac{{9\sqrt 2 }}{2}\) và \({\Delta _2}: x = \frac{{9\sqrt 2 }}{2}\).

b) Hypebol (H): \(\frac{{{x^2}}}{{15}} – \frac{{{y^2}}}{{10}} = 1\), \(c = \sqrt {{a^2} + {b^2}}  = 5\)

+ Tâm sai của hypebol: \(e = \frac{c}{a} = 3\)

+ Tiêu điểm \({F_1}( – 5;0),{F_2}(5;0)\)

+ Đường chuẩn: \({\Delta _1}: x =  – \frac{{\sqrt {15} }}{3}\) và \({\Delta _2}: x = \frac{{\sqrt {15} }}{3}\).

c) Parabol (P): \({y^2} = x\), suy ra \(p = \frac{1}{2}\)

+ Tâm sai \(e = 1\)

+ Tiêu điểm \(F(\frac{1}{4};0)\)

+ Đường chuẩn: \(\Delta : x =  – \frac{1}{4}\)

Giải bài 2 trang 64 Chuyên đề học tập Toán 10 – Chân trời sáng tạoChuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Viết phương trình của đường conic có tâm sai bằng 1, tiêu điểm \(F(1;0)\) và đường chuẩn là \(\Delta : x + 1 = 0\)

Bước 1: Xác định loại đường conic dựa vào tâm sai e:

+ \(0 < e < 1\) thì conic là đường elip

+ \(e = 1\) thì conic là đường parabol

+ \(e > 1\) thì conic là đường hypebol

Bước 2: Tìm tập hợp các điểm M sao cho \(\frac{{MF}}{{d(M,\Delta )}} = e\)

Từ đó kết luận phương trình đường conic.

Lời giải chi tiết

Đường conic có tâm sai bằng 1 thì là parabol.

Điểm \(M(x,y)\) thuộc đường conic khi và chỉ khi

\(\begin{array}{l}\frac{{MF}}{{d(M,\Delta )}} = 1 \Leftrightarrow \frac{{\sqrt {{{\left( {x – 1} \right)}^2} + {y^2}} }}{{\left| {x + 1} \right|}} = 1\\ \Leftrightarrow \sqrt {{{\left( {x – 1} \right)}^2} + {y^2}}  = \left| {x + 1} \right|\\ \Leftrightarrow {\left( {x – 1} \right)^2} + {y^2} = {\left( {x + 1} \right)^2}\\ \Leftrightarrow {y^2} = 4x\end{array}\)

Vậy phương trình đường parabol là \({y^2} = 4x\)

Giải bài 3 trang 64 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Viết phương trình của đường conic (C) trong mỗi trường hợp sau:

a) (C) có tiêu điểm \(F(8;0)\), đường chuẩn là \(\Delta : x – 2 = 0\)và tâm sai \(e = 2\)

b) (C) có tiêu điểm \(F( – 4;0)\), đường chuẩn là \(\Delta : x + \frac{{25}}{4} = 0\)và tâm sai \(e = \frac{4}{5}\)

Bước 1: Xác định loại đường conic dựa vào tâm sai e:

+ \(0 < e < 1\) thì conic là đường elip

+ \(e = 1\) thì conic là đường parabol

+ \(e > 1\) thì conic là đường hypebol

Bước 2: Tìm tập hợp các điểm M sao cho \(\frac{{MF}}{{d(M,\Delta )}} = e\)

Từ đó kết luận phương trình đường conic.

Lời giải chi tiết

a) Đường conic có tâm sai bằng 2 thì là hypebol.

Điểm \(M(x,y)\) thuộc đường conic khi và chỉ khi

\(\begin{array}{l}\frac{{MF}}{{d(M,\Delta )}} = 2 \Leftrightarrow \frac{{\sqrt {{{\left( {x – 8} \right)}^2} + {y^2}} }}{{\left| {x – 2} \right|}} = 2\\ \Leftrightarrow \sqrt {{{\left( {x – 8} \right)}^2} + {y^2}}  = 2\left| {x – 2} \right|\\ \Leftrightarrow {\left( {x – 8} \right)^2} + {y^2} = 4{\left( {x – 2} \right)^2}\\ \Leftrightarrow {y^2} = 3{x^2} – 48\\ \Leftrightarrow \frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{{48}} = 1\end{array}\)

Vậy phương trình đường hypebol là \(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{{48}} = 1\)

b) Đường conic có tâm sai \(e = \frac{4}{5} < 1\) thì là elip

Điểm \(M(x,y)\) thuộc đường conic khi và chỉ khi

\(\begin{array}{l}\frac{{MF}}{{d(M,\Delta )}} = \frac{4}{5} \Leftrightarrow \frac{{\sqrt {{{\left( {x + 4} \right)}^2} + {y^2}} }}{{\left| {x + \frac{{25}}{4}} \right|}} = \frac{4}{5}\\ \Leftrightarrow 5\sqrt {{{\left( {x + 4} \right)}^2} + {y^2}}  = 4\left| {x + \frac{{25}}{4}} \right|\\ \Leftrightarrow 25{\left( {x + 4} \right)^2} + 25{y^2} = 16{\left( {x + \frac{{25}}{4}} \right)^2}\\ \Leftrightarrow 25{y^2} + 9{x^2} = 225\\ \Leftrightarrow \frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\end{array}\)

Vậy phương trình đường elip là \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)

Bài 4 trang 64

---

Đề bài

Quỹ đạo của các vật thể sau đây là những đường conic. Những đường này là elip, parabol hay hypebol?

Tên	Tâm sai
Sao Hỏa	0,0934
Mặt Trăng	0,0549
Sao Thủy	0,2056
Sao chổi Ikeya-Seki	0,9999
C/2019 Q4	3,5

(Nguồn: https://vi.wikipedia.org)

Đường conic có tâm sai e:

+ \(0 < e < 1\) thì conic là đường elip

+ \(e = 1\) thì conic là đường parabol

+ \(e > 1\) thì conic là đường hypebol

Lời giải chi tiết

Tên	Tâm sai	So sánh với 0 và 1	Kết luận
Sao Hỏa	0,0934	0 < 0,0934 < 1	Elip
Mặt Trăng	0,0549	0 < 0,0549 < 1	Elip
Sao Thủy	0,2056	0 < 0,2056 < 1	Elip
Sao chổi Ikeya-Seki	0,9999	\( \approx 1\)	Parabol
C/2019 Q4	3,5	3,5 > 1	Hypebol