Giải bài tập Bài 33 Quan hệ giữa ba cạnh của một tam giác (Chương 9 Toán 7 Kết nối)
============
bài 33 Quan hệ giữa ba cạnh của một tam giác
Giải bài 9.10 trang 69 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Cho các bộ ba đoạn thẳng có độ dài như sau:
a) 2 cm, 3 cm, 5 cm
b) 3 cm, 4 cm, 6 cm
c) 2 cm, 4 cm, 5 cm.
Hỏi bộ ba nào không thể là độ dài ba cạnh của một tam giác? Vì sao? Với mỗi bộ ba còn lại, hãy vẽ một tam giác có độ dài ba cạnh được cho trong bộ ba đó.
Phương pháp giải
Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không
Lời giải chi tiết
Theo bất đẳng thức tam giác:
a) Vì 2 + 3 = 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 3 cm, 5 cm không thể là độ dài ba cạnh của một tam giác
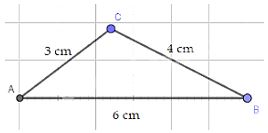
b) Vì 3+4 > 6 nên bộ ba đoạn thẳng có độ dài 3 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác

* Cách vẽ: + Vẽ độ dài cạnh AB = 6cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 3 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.
c) Vì 2+4 > 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 4 cm, 5 cm có thể là độ dài ba cạnh của một tam giác
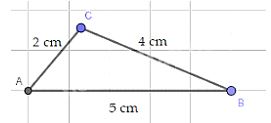
* Cách vẽ: + Vẽ độ dài cạnh AB = 5cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 2 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.
–>
— *****
Giải bài 9.11 trang 69 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
a) Cho tam giác ABC có AB = 1 cm, BC = 7 cm. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên ( cm).
b) Cho tam giác ABC có AB= 2 cm, BC = 6 cm và BC là cạnh lớn nhất. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên ( cm).
Phương pháp giải
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh CA là số nguyên
Lời giải chi tiết
Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:
7 – 1 < CA < 7 + 1
6 < CA < 8
Mà CA là số nguyên
CA = 7 cm.
Vậy CA = 7 cm.
b) Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:
AB + CA > BC
2 + CA > 6
CA > 4 cm
Mà CA là số nguyên và CA < 6 ( vì BC = 6 cm là cạnh lớn nhất của tam giác)
CA = 5 cm
Vậy CA = 5 cm.
–>
— *****
Giải bài 9.12 trang 69 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC. (H.9.18)
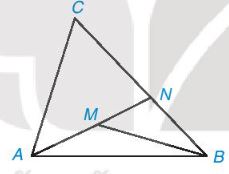
a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB
b) So sánh NA với CA + CN, từ đó suy ra NA + NB < CA + CB
c) Chứng minh MA + MB < CA + CB.
Phương pháp giải
Sử dụng định lí:
+ Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
+ Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất.
Lời giải chi tiết
a) 3 điểm M,N,B không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác MNB có:
MB < MN + NB
MA + MB < MA + MN + NB
MA + MB < NA + NB ( vì MA + MN = NA) (1)
b) 3 điểm A,N,C không thẳng hàng.
Áp dụng bất đẳng thức tam giác trong tam giác ACN có:
NA < CA + CN
NA + NB < CA + CN + NB
NA + NB < CA + CB ( vì CN + NB = CB) (2)
c) Từ (1) và (2) ta có:
MA + MB < NA + NB < CA + CB
Vậy MA + MB < CA + CB
–>
— *****
Giải bài 9.13 trang 69 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
Phương pháp giải
Áp dụng quan hệ giữa ba cạnh của tam giác ABD và tam giác ACD.
Lời giải chi tiết
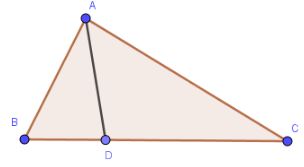
Áp dụng quan hệ giữa ba cạnh của tam giác ABD, ta có: AD < AB + BD
Áp dụng quan hệ giữa ba cạnh của tam giác ACD, ta có: AD < CD + AC
\(\Rightarrow AD + AD < AB+BD+CD+AC\)
\(\Rightarrow 2AD<AB+BC+AC\) ( vì \(DB+DC=BC\))
\(\Rightarrow\) 2AD < Chu vi tam giác ABC hay AD < (Chu vi tam giác ABC) : 2
Vậy AD nhỏ hơn nửa chu vi tam giác ABC.
–>
— *****
