Giải bài tập Bài cuối Chương 9 Toán 7 Kết nối
=============
Giải bài 9.36 trang 84 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Cho tam giác ABC \(\widehat{BAC}\) là góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
Phương pháp giải
DC>DE (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC => \(\widehat{BDC}\) là góc tù (2)
Từ (1) và (2) suy ra: BC>DE
Lời giải chi tiết
Vì \(\widehat{BAC}\) là góc tù nên \(\widehat{ADE}\) , \(\widehat{AED}\) là các góc nhọn
=> \(\widehat{DEC}\) là góc tù.
=>DC>DE (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC có:
\(\widehat{DAC}\) là góc tù nên \(\widehat{ADC}\) , \(\widehat{ACD}\) là các góc nhọn
=> \(\widehat{BDC}\) là góc tù.
=>BC>DC (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
– Từ (1) và (2) suy ra: BC>DE
–>
— *****
Giải bài 9.37 trang 84 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
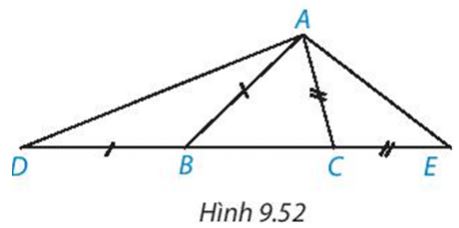
Cho tam giác ABC ( AB> AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa B D và C, C nằm giữa B và E, BD = BA, CE= CA ( H.9.52)
a) So sánh \(\widehat{ADE}\) và \(\widehat{AED}\)
b) So sánh các đoạn thẳng AD và AE

Phương pháp giải
a) AB > AC => \(\widehat{ABC}\) < \(\widehat{ACB}\), tìm số đo \(\widehat{ACE}\), \(\widehat{ABD}\) rồi so sánh
Tam giác ABD cân tại B ( BD= BA) => \(\widehat{ABD}\) = 180°- 2\(\widehat{ADB}\)
Tam giác ACE cân tại C ( CE= CA) => \(\widehat{ACE}\) = 180°- 2\(\widehat{AEC}\)
Tìm số đo hai góc \(\widehat{ADB}\), \(\widehat{AEC}\) rồi so sánh
b) Xét tam giác ADE
Lời giải chi tiết
a) AB > AC => \(\widehat{ABC}\) < \(\widehat{ACB}\) ( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\widehat{ABD}\) + \(\widehat{ABC}\) = 180° => \(\widehat{ABC}\) = 180°- \(\widehat{ABD}\)
\(\widehat{ACE}\) + \(\widehat{ACB}\) = 180° => \(\widehat{ACB}\) = 180°- \(\widehat{ACE}\)
=> 180°- \(\widehat{ABD}\) < 180°- \(\widehat{ACE}\)
=> \(\widehat{ACE}\) < \(\widehat{ABD}\)
Tam giác ABD cân tại B ( BD= BA) => \(\widehat{ABD}\) = 180°- 2\(\widehat{ADB}\)
Tam giác ACE cân tại C ( CE= CA) => \(\widehat{ACE}\) = 180°- 2\(\widehat{AEC}\)
=> 180°- 2\(\widehat{ADB}\) > 180°- 2\(\widehat{AEC}\)
=> \(\widehat{ADB}\) < \(\widehat{AEC}\)
b) Xét tam giác ADE ta có : \(\widehat{ADB}\) < \(\widehat{AEC}\)
=> AD > AE
–>
— *****
Giải bài 9.38 trang 84 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
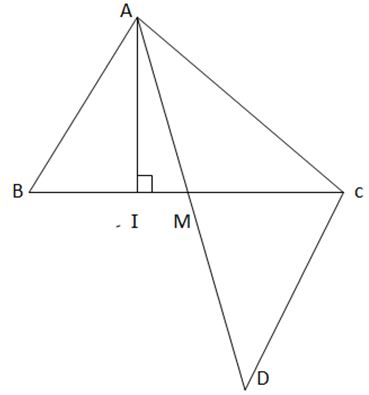
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng
a) AI < \(\frac{1}{2}\) (AB + AC)
b) AM < \(\frac{1}{2}\) (AB + AC)
Phương pháp giải
a) AI là đường cao từ A xuống đoạn thẳng BC
=> AI < AB và AI < AC
Cộng 2 vế với nhau ta có => AI <\(\frac{1}{2}\) (AB + AC)
b) Lấy D sao cho M là trung điểm của AD
Xét ∆ ABM và ∆ DCM, chứng minh ∆ ABM = ∆ DCM
Lời giải chi tiết
a) AI là đường cao từ A xuống đoạn thẳng BC=> AI là khoảng cách từ A đến BC => AI ngắn nhất
=> AI < AB và AI < AC
Cộng 2 vế với nhau ta có : 2 AI < AB + AC
=> AI <\(\frac{1}{2}\) (AB + AC)
b) Lấy D sao cho M là trung điểm của AD
Xét ∆ ABM và ∆ DCM có
AM = DM ( M là trung điểm củaAD)
BM=CM ( M là trung điểm của BC)
\(\widehat{AMB}\) = \(\widehat{CMD}\) (2 góc đối đỉnh)
=> ∆ ABM = ∆ DCM
=>AB = CD
Xét ∆ ADC ta có: AD < AC + CD
=> 2AM < AC + AB
=> AM < \(\frac{1}{2}\) (AB + AC)
–>
— *****
Giải bài 9.39 trang 84 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
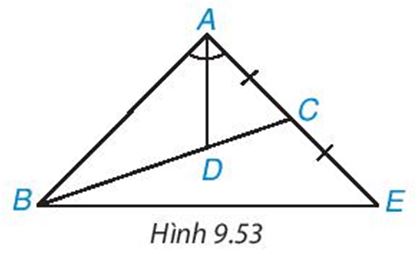
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A
Gợi ý D là trọng tâm của tam gíac ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
Phương pháp giải
D là trọng tâm của tam gíac ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
Lời giải chi tiết
C là trung điểm của AE => BC là trung tuyến của tam giác ABE (1)
D thuộc BC, BD= 2DC
=> BC= BD + DC = 2DC + DC = 3DC => DC = \(\frac{1}{3}\) BC (2)
Từ (1) và (2)=> D là trọng tâm của tam giác ABE
=> AD là đường trung tuyến ứng với BE
mà AD là đường phân giác của \(\widehat{BAC}\) hay \(\widehat{BAE}\) thuộc tam giác ABE
=> Tam giác ABE cân tại A
–>
— *****
