Lý thuyết Bài 1: Dấu của tam thức bậc hai – Chân trời

Lý thuyết Bài 1: Dấu của tam thức bậc hai – Chân trời
============

1.1. Tam thức bậc hai

* Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) \(a \ne 0\). Khi thay x bằng giá trị x₀ vào ƒ(x), ta được \(f\left( {{x_0}} \right) = a{x_0}^2 + b{x_0} + c\), gọi là giá trị của tam thức bậc lai tại x₀.

+ Nếu \(f\left( {{x_0}} \right) > 0\) thì ta nói f(x) đương tại x₀;

+ Nếu \(f\left( {{x_0}} \right) < 0\) thì ta nói f(x) âm tại x_0;

+ Nếu f(x) đương (âm) tại mọi điểm x thuộc một khoảng hoặc một đoạn thì ta nói f{x) dương (âm) trên khoảng hoặc đoạn đó.

* Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\) \(a \ne 0\). Khi đó

+ Nghiệm của phương trình bậc hai \(a{x^2} + bx + c\) là nghiệm của f(x).

+ Biểu thức \(\Delta  = {b^2} – 4{\rm{a}}c\) và \(\Delta ‘ = {\left( {\frac{b}{2}} \right)^2} – ac\) lần lượt là biệt thức và biệt thức thu gọn của f(x).

Ví dụ:  Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét đâu của nó tại x=2

\(\begin{array}{l}
a)f(x) =  – {x^2} + x + 3\\
b)g(x) =  – 3x + \frac{{13}}{2}
\end{array}\)

Giải

a) Biểu thức \(f(x) =  – {x^2} + x + 3\) là một tam thức bậc hai.

\(f(2) =  – {2^2} + 2 + 3 = 1 > 0\) nên f(x) đương tại x= 2.

b) Biểu thức \(g(x) =  – 3x + \frac{{13}}{2}\) không phải lả một tam thức bậc hai

1.2. Định lí về dấu của tam thức bậc hai

Chú ý

a) Để xét dâu tam thức bậc hai \(f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)\), ta thực hiện các bước sau:

Bước 1: Tỉnh và xác định đâu của biệt thức \(\Delta \);

Bước 2: Xác định nghiệm của ƒ(x) (nếu có);

Bước 3: Xác định đâu của hệ sô a,

Bước 4: Xác định dâu của ƒ(x)

b) Khi xét dấu của tam thức bậc hai, ta có thể đùng biệt thúc thu gọn \(\Delta ‘\) thay cho biệt thức \(\Delta\).

Ví dụ

Xét dẫu của tam thức bậc hai sau: \(f(x) =  – {x^2} + 3{\rm{x}} + 10\)

Giải

\(f(x) =  – {x^2} + 3{\rm{x}} + 10\) \(\Delta \) = 49 > 0, hai nghiệm phân biệt là x₁ = -2, x₂ = 5 và a = – 1 < 0

Ta có bảng xét dấu f(x) như sau:

Vậy f(x) dương trong khoảng (-2; 5) và âm trong hai khoảng \(\left( { – \infty ; – 2} \right)\) và \(\left( {5; + \infty } \right)\).

Câu 1:  Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại \(x = 1\).

a) \(f\left( x \right) = 2{x^2} + x – 1\);

b) \(g\left( x \right) =  – {x^4} + 2{x^2} + 1\)

c) \(h\left( x \right) =  – {x^2} + \sqrt 2 .x – 3\)

Hướng dẫn giải

a) Biểu thức \(f\left( x \right) = 2{x^2} + x – 1\) là một tam thức bậc hai

\(f\left( 1 \right) = {2.1^2} + 1 – 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)

b) Biểu thức \(g\left( x \right) =  – {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai

c) Biểu thức \(h\left( x \right) =  – {x^2} + \sqrt 2 .x – 3\) là một tam thức bậc hai

\(h\left( 1 \right) =  – {1^2} + \sqrt 2 .1 – 3 = \sqrt 2  – 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)

Câu 2:  Xét dấu của các tam thức bậc hai sau:

a) \(f\left( x \right) = 2{x^2} – 3x – 2\)         

b) \(g\left( x \right) =  – {x^2} + 2x – 3\)

Hướng dẫn giải

a) \(f\left( x \right) = 2{x^2} – 3x – 2\) có \(\Delta  = 25 > 0\), hai nghiệm phân biệt là \({x_1} =  – \frac{1}{2};{x_2} = 2\)

và \(a = 2 > 0\)

Ta có bảng xét dấu như sau:

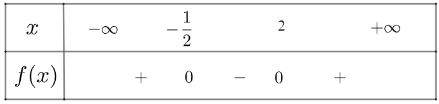
Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { – \frac{1}{2},2} \right)\) và dương trong hai khoảng

 \(\left( { – \infty , – \frac{1}{2}} \right)\) và \(\left( {2, + \infty } \right)\)

b) \(g\left( x \right) =  – {x^2} + 2x – 3\) có \(\Delta  = {2^2} – 4.\left( { – 1} \right).\left( { – 3} \right) =  – 8 < 0\) và \(a =  – 1 < 0\)

Vậy \(g\left( x \right)\)âm với mọi \(x \in \mathbb{R}\)

===========
Chuyên mục: Chương 7: Bất phương trình bậc hai một ẩn