Lý thuyết Bài tập cuối chương 6 – Chân trời

Lý thuyết Bài tập cuối chương 6 – Chân trời
============

1.1. Số gần đúng và sai số

a) Số gần đúng, sai số tuyệt đối, sai số tương đối

* Sai số tuyệt đối

+) Sai số tuyệt đối của số gần đúng a: \({\Delta _a} = \;|a – \overline a |\)

Ý nghĩa: Phản ánh mức độ sai lệch giữa số đúng \(\overline a \) và số gần đúng \(a\).

Ta viết:  \(\overline a  = a \pm d\) hoặc \(a – d \le \overline a  \le a + d\) hoặc \(\overline a  \in [a – d;a + d]\)

+) Đánh giá sai số tuyệt đối: \({\Delta _a} \le d\) (\(d\) gọi là độ chính xác của số gần đúng)

* Sai số tương đối

Trong các phép đo không tương đồng, người ta sử dụng sai số tương đối.

+) Sai số tương đối của số gần đúng a: \({\delta _a} = \frac{{{\Delta _a}}}{{|a|}} \le \frac{d}{{|a|}}\)

Ý nghĩa: Sai số tương đối càng nhỏ thì chất lượng của phép đo hay tính toán càng cao.

b) Số quy tròn

Quy tắc làm tròn số +) Nếu chữ số sau hàng quy tròn nhỏ hơn 5 thì ta thay nó và các chữ số bên phải nó bởi chữ số 0. +) Nếu chữ số sau hàng quy tròn lớn hơn hoặc bằng 5 thì ta cũng làm như trên nhưng cộng thêm 1 đơn vị vào chữ số hàng quy tròn.

Chú ý:

– Khi thay số đúng bởi sô quy tròn đến một hàng nào đó thì sai số tuyệt đổi của số quy tròn không vượt quá nửa đơn vị của hàng quy tròn. Ta cỏ thể nói đô chính xác của số quy tròn băng nửa đơn vị của hàng quy tròn.

– Khi quy tròn số đúng \(\overline a \) đến một hàng nào đó thì ta nói sô gần đúng a nhân được là chính xác đền hàng đó. Ví dụ số gần đúng của \(\pi \) chính xác đền hàng phân trăm là 3,14

* Xác định số quy tròn của số gần đúng a với độ chính xác d cho trước:

Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d.

Bước 2: Quy tròn a ở hàng gấp 10 lần hàng tìm đc ở trên.

* Xác định số gần đúng của một số với độ chính xác d cho trước:

Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d.

Bước 2: Quy tròn \(\overline a \) đến hàng tìm đc ở trên.

1.2. Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

a) Số trung bình

Cho mẫu số liệu \({x_1},{x_2},{x_3},…,{x_n}\)

+) Số trung bình (hay TB cộng) của mẫu số liệu kí hiệu là \(\overline x \), được tính bằng công thức: \(\overline x  = \frac{{{x_1} + {x_2} + {x_3} + … + {x_n}}}{n}\) +) Mẫu số liệu cho dưới dạng bảng tần số thì: \(\overline x  = \frac{{{n_1}{x_1} + {n_2}{x_2} + {n_3}{x_3} + … + {n_k}{x_k}}}{n}\)

Với \({n_i}\) là tần số của giá trị \({x_i}\) và \(n = {n_1} + {n_2} + … + {n_k}\)

Ý nghĩa: Số trung bình dùng để đại diện cho các số liệu của mẫu. Nó là một số đo xu thế trung tâm của mẫu đó.

b) Trung vị và tứ phân vị

* Trung vị

+) Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác), ta dùng trung vị để đo xu thế trung tâm. +) Tìm trung vị \({M_e}\): Bước 1: Sắp xếp các giá trị theo thứ tự không giảm \({X_1},{X_2},..,{X_n}\) Bước 2: Cỡ mẫu = n. + Nếu n lẻ (\(n = 2k – 1\)) thì \({M_e} = {X_k}\) + Nếu n chẵn (\(n = 2k\)) thì \({M_e} = \frac{1}{2}({X_k} + {X_{k + 1}})\)

+) Ý nghĩa: Trung vị là giá trị ở vị trí chính giữa của mẫu số liệu đã sắp xếp theo thứ tự không giảm. Trung vị không bị ảnh hưởng bởi giá trị bất thường như số trung bình.

* Tứ phân vị

Tứ phân vị gồm 3 giá trị \({Q_1},{Q_2},{Q_3}\), nó chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành 4 phần, mỗi phần đều chứa 25

+) Các bước tìm tứ phân vị: Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm. Bước 2: Tìm trung vị, chính là \({Q_2}\) Bước 3: \({Q_1}\) là trung vị của nửa số liệu bên trái \({Q_2}\)(không bao gồm \({Q_2}\) nếu n lẻ). Bước 4: \({Q_3}\)là trung vị của nửa số liệu bên phải \({Q_2}\)(không bao gồm \({Q_2}\) nếu n lẻ).

Chú ý

\({Q_1}\) còn được gọi là tứ phân vị thứ nhất hoặc tứ phân vị dưới, đại diện cho nửa mẫu số liệu phía dưới.

 \({Q_3}\) còn được gọi là tứ phân vị thứ ba hoặc tứ phân vị trên, đại diện cho nửa mẫu số liệu phía trên.

c) Mốt

Mốt của mẫu số liệu là giá trị xuất hiện nhiều nhất trong mẫu. Ý nghĩa: Dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu có nhiều giá trị trùng nhau.

Nhận xét

– Mốt có thể không là duy nhất. Một mẫu có thể có nhiều mốt

– Khi các giá trị trong mẫu xuất hiện với tần số như nhau thì mẫu số liệu đó không có mốt.

1.3. Các số đặc trưng đo mức độ phân tán

a) Khoảng biến thiên và khoảng tứ phân vị

– Khoảng biến thiên (R) = Giá trị lớn nhất – Giá trị nhỏ nhất. – Khoảng tứ phân vị:  \({\Delta _Q} = {Q_3} – {Q_1}\)

Ý nghĩa:

– Dùng để đo độ phân tán của toàn bộ mẫu số liệu: Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

– Dùng để đo độ phân tán của một nửa các số liệu có giá trị thuộc đoạn từ \({Q_1}\) đến \({Q_3}\) trong mẫu.

– Không bị ảnh hưởng bởi các giá trị bất thường.

Giá trị ngoại lệ: \(x\) là giá trị ngoại lệ nếu \(\left[ \begin{array}{l}x < {Q_1} – 1,5.{\Delta _Q}\\x > {Q_3} + 1,5.{\Delta _Q}\end{array} \right.\)

b) Phương sai và độ lệch chuẩn

Cho mẫu số liệu \({x_1},{x_2},{x_3},…,{x_n}\), số trung bình là \(\overline x \) + Phương sai: \({s^2} = \frac{{{{({x_1} – \overline x )}^2} + {{({x_2} – \overline x )}^2} + … + {{({x_n} – \overline x )}^2}}}{n} = \frac{1}{n}({x_1}^2 + {x_2}^2 + … + {x_n}^2) – {\overline x ^2}\) + Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)

Ý nghĩa: Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn

Chú ý: Phương sai của mẫu số liệu cho dạng bảng tần số:

\({s^2} = \frac{{{m_1}{{({x_1} – \overline x )}^2} + {m_2}{{({x_2} – \overline x )}^2} + … + {m_k}{{({x_k} – \overline x )}^2}}}{n}\)

Với \({m_i}\) là tần số của giá trị \({x_i}\) và \(n = {m_1} + {m_2} + … + {m_k}\)

* Giả sử mẫu số liệu được cho dưới dạng bảng tần số:

Khi đó, công thức tính phương sai trở thành:

\({S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{x_1} – \overline x } \right)}^2} + {n_2}{{\left( {{x_2} – \overline x } \right)}^2} + … + {n_k}{{\left( {{x_k} – \overline x } \right)}^2}} \right]\)

trong đó n = n1 + n2 +…+ nk

Có thể biến đổi công thức tính phương sai trên thành:

\({S^2} = \frac{1}{n}\left( {{n_1}.x_1^2 + {n_2}.x_2^2 + … + {n_k}.x_k^2} \right) – {\overline x ^2}\). 

Câu 1: Cho biết \(1,41 < \sqrt 2  < 1,42.\) Hãy tính độ dài đường chéo của một hình vuông có cạnh bằng 10 cm và xác định độ chính xác của kết quả tìm được.

Hướng dẫn giải

Ta có: \(1,41 < \sqrt 2  < 1,42\) hay \(1,415 – 0,005 < \sqrt 2  < 1,415 + 0,005\)

\( \Rightarrow \) Số gần đúng của \(\sqrt 2 \) là 1,415 với độ chính xác 0,005

Khi đó: Độ dài đường chéo của hình vuông cạnh 10 cm là: \(10.1,415 = 14,15\;(cm)\)

Độ dài đúng là \(10\sqrt 2 \)cm, thỏa mãn: \(10.1,41 < 10\sqrt 2  < 10.1,42\) hay \(14,1 < 10\sqrt 2  < 14,2\)

Do đó \(14,1 – 14,15 < 10\sqrt 2  – 14,15 < 14,2 – 14,15\), tức là \(\left| {10\sqrt 2  – 14,15} \right| < 0,05.\)

Vậy kết quả 14,15 cm có độ chính xác là 0,05.

Câu 2: Bình vẽ biểu đồ biểu thị tỉ lệ số lượng mỗi loại gia cầm trong một trang trại theo bảng thông kê dưới đây:

 

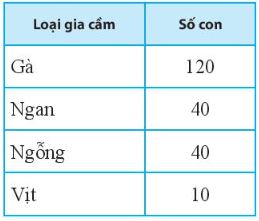
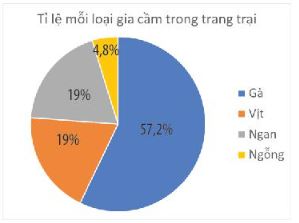
Bạn hãy cho biết biểu đồ Bình vẽ đã chính xác chưa. Nêu chưa thì cần điều chỉnh lại như thê nào cho đúng?

Hướng dẫn giải

Theo bảng thông kê thì số ngan và ngỗng bằng nhau nên trên biểu đồ quạt, hình quạt biểu diễn tỉ lệ ngan và ngỗng phải bằng nhau. Do đó biểu đồ Bình vẽ chưa chính xác.

Nếu ở phần chú giải, Bình đổi chỗ “Vịt” và “Ngống” thì sẽ được biểu đồ chính xác.

Câu 3: Hãy tìm tứ phân vị của các mẫu số liệu sau:

a) 10; 13; 15; 2; 10; 19; 2; 5; 7

b) 15; 19; 10; 5; 9; 10; 1; 2; 5; 15

Hướng dẫn giải

a) Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được:

2; 2; 5; 7; 10; 10; 13; 15; 19

+) Vì cỡ mẫu là \(n = 9\), là số lẻ, nên giá trị tứ phân vị thứ hai là \({Q_2} = 10\)

+) Tứ phân vị thứ nhất là trung vị của mẫu: 2; 2; 5; 7.

Do đó \({Q_1} = \frac{1}{2}(2 + 5) = 3,5\)

+) Tứ phân vị thứ nhất là trung vị của mẫu: 10; 13; 15; 19.

Do đó \({Q_3} = \frac{1}{2}(13 + 15) = 14\)

b) Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được:

1; 2; 5; 5; 9; 10; 10; 15; 15; 19

+) Vì cỡ mẫu là \(n = 10\), là số chẵn, nên giá trị tứ phân vị thứ hai là \({Q_2} = \frac{1}{2}(9 + 10) = 9,5\)

+) Tứ phân vị thứ nhất là trung vị của mẫu: 1; 2; 5; 5; 9.

Do đó \({Q_1} = 5\)

+) Tứ phân vị thứ nhất là trung vị của mẫu: 10; 10; 15; 15; 19.

Do đó \({Q_3} = 15\)

Câu 4: Bảng dưới đây thống kê tổng số giờ nắng trong năm 2019 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở Tuyên Quang và Cà Mau.

Tháng

1

2

3

4

5

6

7

8

9

10

11

12

Tuyên Quang

25

89

72

117

106

177

156

203

227

146

117

145

Cà Mau

180

223

257

245

191

111

141

134

130

122

157

173

a) Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh.

b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh.

Hướng dẫn giải

+) Tuyên Quang:

Số giờ nắng trung bình \(\overline x  = \frac{{25 + 89 + 72 + 117 + 106 + 177 + 156 + 203 + 227 + 146 + 117 + 145}}{{12}} = 131,67\)

Phương sai: \({S^2} = \frac{1}{{12}}\left( {{{25}^2} + {{89}^2} + … + {{145}^2}} \right) – 131,{67^2} \approx 2921,2\)

Độ lệch chuẩn \(S = \sqrt {2921,2}  \approx 54\)

+) Cà Mau:

Số giờ nắng trung bình \(\overline x  = \frac{{180 + 223 + 257 + 245 + 191 + 111 + 141 + 134 + 130 + 122 + 157 + 173}}{{12}} = 172\)

Phương sai: \({S^2} = \frac{1}{{12}}\left[ {\left( {{{180}^2} + {{223}^2} + … + {{173}^2}} \right) – {{172}^2}} \right] = 2183\)

Độ lệch chuẩn \(S = \sqrt {2183}  = 46,7\)

=> Nhận xét: Ở Tuyên Quang tổng số giờ nắng theo từng tháng thay đổi nhiều hơn so với ở Cà Mau.

===========
Chuyên mục: Chương 6: Thống kê