Trả lời câu hỏi trong bài 2 Hệ bất phương trình bậc nhất hai ẩn – Chân trời

Trả lời câu hỏi trong bài 2 Hệ bất phương trình bậc nhất hai ẩn – Chân trời
============

KHỞI ĐỘNG

Hai đường thẳng d: = -x – 2 và d’: y = x + 1 chia mặt phẳng tọa độ thành bốn miền khác nhau (không tính đường thẳng d và d’) như hình bên.

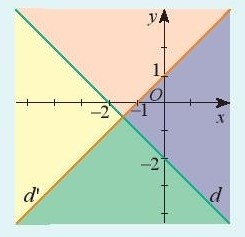
Để kí hiệu một trong bốn miền đó, người ta đã tạo nhãn:

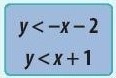
Hãy đặt nhãn này vào miền phù hợp.

Hướng dẫn giải:

1. KHÁI NIỆM VỀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Khám phá 1:  Một người nông dân dự định quy hoạch x sào đất trồng cà tím vfa y sào đất trồng cà chua. Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng. 

a. Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y.

b. Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên? 

(20; 40), (40; 20); (-30; 10).

Hướng dẫn giải:

a. $\left\{\begin{matrix} 0,2x + 0,1y \leq 9\\ x \geq 0\\y \geq 0\end{matrix}\right.$

b. Cặp số (20; 40) thỏa mãn đồng thời tất cả các bất phương trình nêu trên.

Thực hành 1:  Hãy chỉ ra hai nghiệm của bất phương trình trong Ví dụ 1.

Hướng dẫn giải:

a. $\left\{\begin{matrix}  3x + y – 1 \leq 0\\ 2x – y + 2 \geq  0\end{matrix}\right.$

(0; 0) và (0; 1) là hai nghiệm của bất phương trình trên.

b. $\left\{\begin{matrix} y – 1 < 0\\ x + 2 \geq  0\end{matrix}\right.$

(0; 0) và (1; -1) là hai nghiệm của bất phương trình trên.

c. $\left\{\begin{matrix} x + y – 3 \leq 0\\ -2x + y + 3 \geq 0\\ x \geq 0\\ y \geq 0\end{matrix}\right.$

(0; 1) và ( 1; 1) là hai nghiệm của bất phương trình trên.

2. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

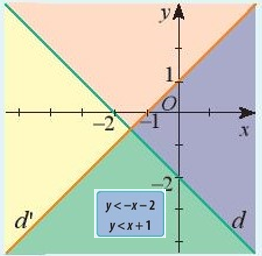
Khám phá 2:  Cho hệ bất phương trình: $\left\{\begin{matrix} x + y – 3 \leq 0\\ -2x + y + 3 \geq 0\end{matrix}\right.$

Miền nào trong Hình 1 biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho?

Hướng dẫn giải:

Miền không gạch chéo trong hình 1 là miền nghiệm của hệ bất phương trình trên.

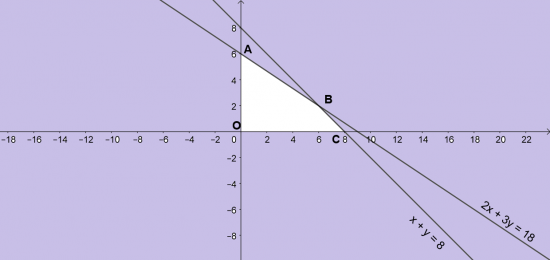
Thực hành 2:  Biểu diễn miền nghiệm của hệ bất phương trình: $\left\{\begin{matrix} x + y \leq  8\\ 2x + 3y \leq 18\\ x \geq 0\\ y \geq 0\end{matrix}\right.$

Hướng dẫn giải:

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.

Miền không tô màu (miền tứ giác OABC, bao gồm các cạnh) là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

3. TÌM GIÁ TRỊ LỚN NHẤT HOẶC GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC F = ax + by TRÊN MỘT MIỀN ĐA GIẮC

Vận dụng: Một người bán nước giải khát đang có 24g bột cam, 9l nước và 210g đường để pha chế hai loại nước cam A và B. Để pha chế 1l nước cam loại A cần 30g đường, 1l nước và 1g bột cam; để pha chế 1l nước cam loại B cần 10g đường, 1l nước và 4g bột cam. Mỗi lít nước cam loại A bán được 60 nghìn đồng, mỗi lít nước cam loại B bán được 80 nghìn đồng. Người đó nên pha chế bao nhiêu lít nước cam mỗi loại để có doanh thu cao nhất?

Hướng dẫn giải:

Tóm tắt bài toán:

Gọi x là số lít nước cam loại A pha chế được, y là số lít nước cam phá chế được. Ta có hệ bất phương trình: $\left\{\begin{matrix} x + 4y \leq  24\\ 3x + 1y \leq 21\\ x + y \leq 9\\ x \geq 0\\ y \geq 0\end{matrix}\right.$

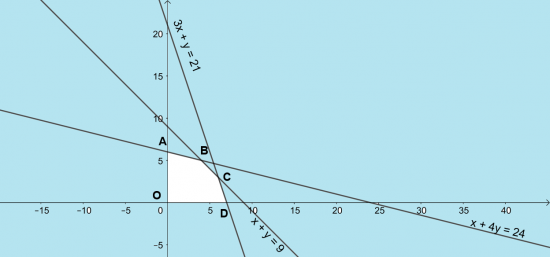
Ta có điểm B là giao điểm của đường thẳng x + y = 9 và x + 4y = 24 nên tọa độ điểm B là 

$\left\{\begin{matrix} x + y = 9\\ x + 4y = 24\end{matrix}\right.$ <=> $\left\{\begin{matrix} x = 4\\ y = 5\end{matrix}\right.$

Ta có điểm C là giao điểm của đường thẳng x + y = 9 và 3x + y = 21 nên tọa độ điểm C là:

$\left\{\begin{matrix} x + y = 9\\ 3x + y = 21\end{matrix}\right.$ <=> $\left\{\begin{matrix} x = 6\\ y = 3\end{matrix}\right.$

Miền nghiệm của hệ bất phương trình là miền ngũ giác OABCD với các đỉnh O(0; 0); A(0, 6); B( 4; 5); C(6;3); D(7; 0).

Gọi F là số tiền lãi (đơn vị: nghìn đồng) thu được: F = 60x + 80y 

Tính giá trị của F tại các đỉnh của ngũ giác:

• Tại O(0;0): F = 60. 0 + 80. 0 = 0
• Tại A(0; 6): F = 60. 0 + 80. 6 = 480
• Tại B(4; 5): F = 60. 4 + 80. 5 = 640
• Tại C(6; 3): F = 60. 6 + 80. 3 = 600
• Tại D(7;0): F = 60. 7 + 80. 0 = 420

F đạt giá trị lớn nhất bằng 640 nghìn đồng tại B(4; 5).

Vậy cần sản xuất 4 lít nước cam loại A và 5 lít nước cam loại B để có lãi cao nhất.

===========
Chuyên mục: Học Toán lớp 10 – Chân trời