Lý thuyết Bài tập cuối chương 2 – Chân trời

Lý thuyết Bài tập cuối chương 2 – Chân trời
============

1.1. Bất phương trình bậc nhất hai ẩn

a) Khái niệm bất phương trình bậc nhất hai ẩn

Bất phương trình bậc nhất hai ẩn x, y là BPT có một trong các dạng \(ax + by + c \le 0\;;ax + by + c \ge 0;ax + by + c < 0;ax + by + c > 0\) trong đó a, b, c là những số cho trước, a và b không đồng thời bằng 0, x và y là các ẩn.

b) Nghiệm của bất phương trình bậc nhất hai ẩn

Xét bất phương trình: \(ax + by + c < 0\). 

Mỗi cặp số \(({x_0};{y_0})\) thỏa mãn \(a{x_0} + b{y_0} + c\; < 0\) được gọi là một  nghiệm  của BPT đã cho.

Chú ý:

Nghiệm của các bất phương, trình \(ax + by + c < 0,ax + by + c \le 0,ax + by + c \ge 0\) được định nghĩa tương tự.

c) Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn

+) Trong mặt phẳng tọa độ Oxy, tập hợp các điểm \(({x_0};{y_0})\) sao cho \(a{x_0} + b{y_0} + c < 0\) được gọi là miền nghiệm của bất phương trình \(ax + by + c < 0\).

+) Biểu diễn miền nghiệm của BPT \(ax + by + c < 0\)

Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng \(\Delta :ax + by + c = 0\).

Bước 2: Lấy một điểm \(M({x_0};{y_0})\) không thuộc \(\Delta .\) Tính \(a{x_0} + b{y_0} + c\)

Bước 3: Kết luận

– Nếu \(a{x_0} + b{y_0} + c < 0\) thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ \(\Delta \)) chứa điểm \(M\).

– Nếu \(a{x_0} + b{y_0} + c > 0\) thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ \(\Delta \)) không chứa điểm \(M\).

Chú ý:

Đỗi với các bất phương trình bậc nhất hai ẩn dang \(ax + by + c \le 0\) (hoặc \(ax + by + c \ge 0\)) thì miền nghiệm là miền nghiệm của bất phương trình ax + by + c < 0 (hoặc ax + by + c > 0) kể cả bờ.

1.2. Hệ bất phương trình bậc nhất hai ẩn

a) Khái niệm hệ bất phương trình bậc nhất hai ẩn

Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của tất cả các bắt phương trình đó được gọi là một nghiệm của hệ bât phương trình đã cho. Trên mặt phẳng toạ độ Oxy, tập hợp các điểm (x0; y0) có toa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trình đó.

b) Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ

Để  biểu diễn miễn nghiệm  của hệ bật phương trình bậc nhật hai ẩn trên mặt phẳng toạ độ Oxy, ta thực hiện như sau:

– Trên cùng mặt phẳng tọa đô, biểu diễn miền nghiệm của mỗi bắt phương trình của hê.

– Phần giao của các miền nghiệm là miền nghiệm của hệ bất phương trình.

c) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác

Cho hệ BPT bậc nhất hai ẩn x, y có miền nghiệm là miền đa giác \({A_1}{A_2}…{A_n}\).

Khi đó: Giá trị lớn nhất (hay nhỏ nhất) của biể thức \(F(x;y) = mx + ny\), với \((x;y)\) là tọa độ các điểm thuộc miền đa giác \({A_1}{A_2}…{A_n}\), đạt được tại một trong các đỉnh của đa giác đó.

Câu 1: Cặp số nào sau đây là nghiệm của bất phương trình \(4x – 7y – 28 \ge 0?\)

a) \((9;1)\)

b) \((2;6)\)

c) \((0; – 4)\)

Hướng dẫn giải

a) Vì \(4.9 – 7.1 – 28 = 1 \ge 0\)nên \((9;1)\) là nghiệm của bất phương trình \(4x – 7y – 28 \ge 0.\)

b) Vì \(4.2 – 7.6 – 28 =  – 62 < 0\)nên \((2;6)\) không là nghiệm của bất phương trình \(4x – 7y – 28 \ge 0.\)

c) Vì \(4.0 – 7.( – 4) – 28 = 0 \ge 0\)nên \((0; – 4)\) là nghiệm của bất phương trình \(4x – 7y – 28 \ge 0.\)

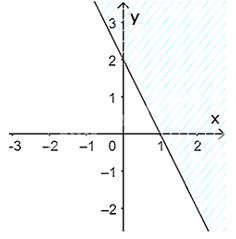
Câu 2: Biểu diễn miền nghiệm của bất phương trình sau: \(2x + y – 2 \le 0\)

Hướng dẫn giải

Vẽ đường thẳng \(\Delta :2x + y – 2 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1;0} \right)\)

Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(2.0 + 0 – 2 =  – 2 < 0\)

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O

(miền không gạch chéo trên hình)

 

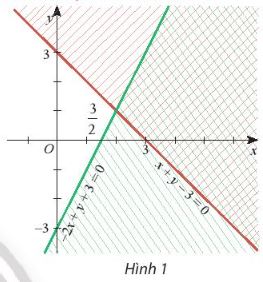
Câu 3: Cho hệ bất phương trình: \(\left\{ \begin{array}{l}x + y – 3 \le 0\\ – 2x + y + 3 \ge 0\end{array} \right.\)

Miền nào trong Hình 1 biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho?

 

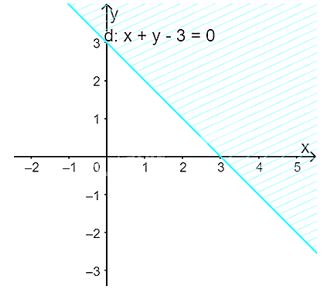
Hướng dẫn giải

Vẽ đường thẳng \(d:x + y – 3 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( {1;2} \right)\)

Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 0 – 3 =  – 3 < 0\)

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(d\), chứa gốc tọa độ O

(miền không gạch chéo trên hình)

Vẽ đường thẳng \(d’: – 2x + y + 3 = 0\) đi qua hai điểm \(A(1; – 1)\) và \(B\left( {2;1} \right)\)

Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( – 2.0 + 0 + 3 = 3 > 0\)

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d’\), chứa gốc tọa độ O

(miền không gạch chéo trên hình)

 

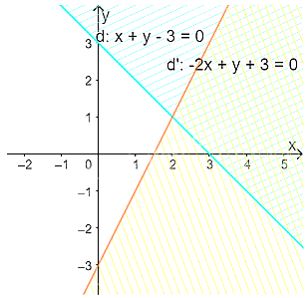
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho.

===========
Chuyên mục: Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn