Lý thuyết Bài tập cuối chương 6
=============
Tóm tắt lý thuyết
1.1. Hàm số
a) Khái niệm hàm số
Nếu với mỗi giá tị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực R thì ta có một hàm số.
Ta gọi x là biến số và y là hàm số của x.
Tập hợp D gọi là tập xác định của hàm số.
Tập tắt cả các giá trị y nhận được, gọi là tập giá trị của hàm số.
b) Đồ thị của hàm số
Đồ thị hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng toạ độ với mọi x thuộc D.
c) Sự đồng biến, nghịch biến của hàm số
Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a; b), nếu
\(\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu
\(\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
1.2. Hàm số bậc hai
a) Khái niệm hàm số bậc hai
Hàm số bậc hai là hàm số cho bởi công thức: \(y = a{x^2} + bx + c\)
trong đó x là biến số, a, b, c là các hằng số và \(a \ne 0\).
Tập xác định của hàm số bậc hai là R.
b) Đồ thị của hàm số bậc hai
+ Đồ thị hàm số y = ax2 + bx + c \(\left( {a \ne 0} \right)\) là một đường parabol có đỉnh là điểm \(I\left( { – \frac{b}{{2{\rm{a}}}}; – \frac{\Delta }{{4{\rm{a}}}}} \right)\) có trục đối xứng là đường thẳng \({x = – \frac{b}{{2{\rm{a}}}}}\). Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
+ Để vẽ đường parabol y = ax2 + bx + c ta tiến hành theo các bước sau:
- Bước 1. Xác định toạ độ đính \(I\left( { – \frac{b}{{2{\rm{a}}}}; – \frac{\Delta }{{4{\rm{a}}}}} \right)\);
- Bước 2. Vẽ trục đối xứng \({x = – \frac{b}{{2{\rm{a}}}}}\);
- Bước 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol;
- Bước 4. Vẽ parabol.
1.3. Dấu của tam thức bậc hai
a) Dấu của tam thức bậc hai
– Tam thức bậc hai (đối với x) là biểu thức có dạng ax2 + bx + c, trong đó a, b, c là những số thực cho trước (với \(a \ne 0\)), được gọi là các hệ số của tam thức bậc hai.
– Cho tam thức bậc hai f(x) = ax2+ bx + c (\(a \ne 0\)).
+ Nếu \(\Delta < 0\) thì f(x) cùng dẫu với hệ số a với mọi \(x \in R\).
+ Nếu \(\Delta = 0\) thì f(x) cùng dấu với hệ số a với mọi \(x \ne – \frac{b}{{2{\rm{a}}}}\) và \(f\left( { – \frac{b}{{2{\rm{a}}}}} \right) = 0\).
+ Nếu \(\Delta > 0\) thi tam thức f(x) có hai nghiệm phân biệt x1 và x2 \(\left( {{x_1} < {x_2}} \right)\). Khi đó f(x) cùng dấu với hệ số a với mọi \(x \in \left( { – \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\); f(x) trái dấu với hệ số a với mọi \(x \in \left( {{x_1};{x_2}} \right)\).
b) Bất phương trình bậc hai
+ Bất phương trình bậc hai ẩn x là bất phương trình có dạng ax2+ bx + c > 0 (hoặc ax2+ bx + c > 0, ax2+ bx + c < 0, \(a{x^2} + bx + c \le 0\)), trong đó a, b, c là những số thực đã cho và \(a \ne 0\).
+ Số thực x0 gọi là một nghiệm của bất phương trình bậc hai ax2+ bx + c > 0, nếu ax2+ bx + c > 0. Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai ax2+ bx + c > 0 gọi là tập nghiệm của bắt phương trình này.
+ Giải bất phương trình bậc hai f(x)= ax2+ bx + c > 0 là tìm tập nghiệm của nó, tức là tìm các khoảng mà trong đó f(x) cùng dấu với hệ số a (nếu a > 0) hay trái dầu với hệ số a (nếu a < 0).
1.4. Phương trình quy về phương trình bậc hai
a) Phương trình dạng \(\sqrt{ax^{2}+bx+c}=\sqrt{dx^{2}+ex+f}\)
Đề giải phương trình \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \), ta thực hiện như sau:
– Bình phương hai về và giải phương trình nhận được;
– Thử lại các giá trị x tìm được ở trên có thoả mãn phương trình đã cho hay không và kết luận nghiệm.
b) Phương trình dạng \(\sqrt{ax^{2}+bx+c}= dx+e\)
Để giải phương trình \(\sqrt{ax^{2}+bx+c}= dx+e\), ta thực hiện như sau:
– Bình phương hai vế và giải phương trình nhận được;
– Thử lại các giá trị x tìm được ở trên có thoả mãn phương trình đã cho hay không và kết luận nghiệm.
Bài tập minh họa
Câu 1: Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giấy) theo công thức: h = \(19,6-4,9t^{2}\); \(h, t\geq 0\).
a. Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b. Tìm tập xác định và tập giá trị của hàm số h.
Hướng dẫn giải
a. Viên bị chạm đất khi h = 0
Hay \(19,6-4,9t^{2}=0\)
\(\Leftrightarrow 4,9t^{2}=19,6\\\Leftrightarrow t^{2}=4\\\Rightarrow t=2\) (do \(t\geq 0\).)
Vậy sau 2 giây kể từ khi rơi viên bi chạm đất.
b. Tập xác định: D = \([0; +\infty )\)
Ta có: \(t^{2}\geq 0\Rightarrow 19,6-4,9t^{2}\leq 19,6\)
Tập giá trị: \([0;19,6]\).
Câu 2: Giải các bất phương trình bậc hai sau:
a) \(-5x^{2}+x-1\leq 0\)
b) \(x^{2}-8x+16\leq 0 \)
c) \(x^{2}-x+6> 0 \)
Hướng dẫn giải
a) Tam thức f(x) = \(-5x^{2}+x-1\) có \( \Delta = -19<0\), a = -5 < 0 nên f(x) luôn âm. Suy ra bất phương trình luôn đúng.
Vậy tập nghiệm bất phương trình là S = \(\mathbb{R}\)
b) Tam thức f(x) = \(x^{2}-8x+16\) có \(\Delta =0\) và a = 1 > 0 nên f(x) \(\geq >0\) với mọi \(x\in \mathbb{R}\).
Suy ra bất phương trình có nghiệm duy nhất x = 4.
c) Tam thức f(x) = \(x^{2}-x+6\) \(\Delta = -23<0\), a = 1 > 0 nên f(x) luôn dương. Suy ra bất phương trình luôn đúng.
Vậy tập nghiệm bất phương trình là S = \(\mathbb{R}\).
Câu 3: Vẽ đồ thị của hàm số y = 3x + 1 và \(y = -2x^{2}\). Hãy cho biết:
a. Hàm số y = 3x + 1 đồng biến hay nghịch biến trên \(\mathbb{R}\).
b. Hàm số \(y =-2x^{2}\) đồng biến hay nghịch biến trên mỗi khoảng \((-\infty ;0)\) và \((0; +\infty)\).
Hướng dẫn giải
Đồ thị hàm số y = 3x + 1:
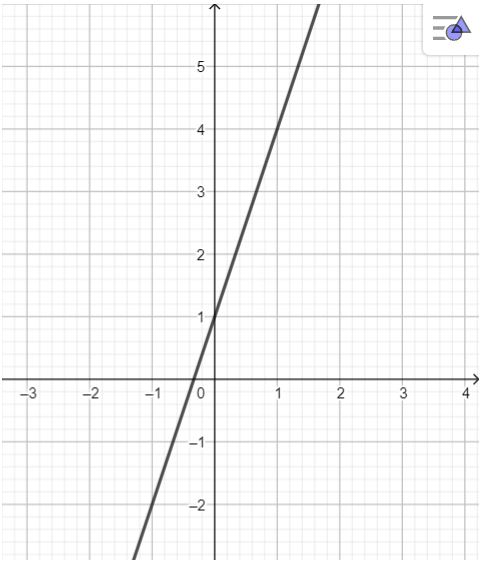
Hàm số đồng biến trên \(\mathbb{R}\), vì giá trị của x tăng thì giá trị của y tăng.
b. Đồ thị hàm số \(y =-2x^{2}\):
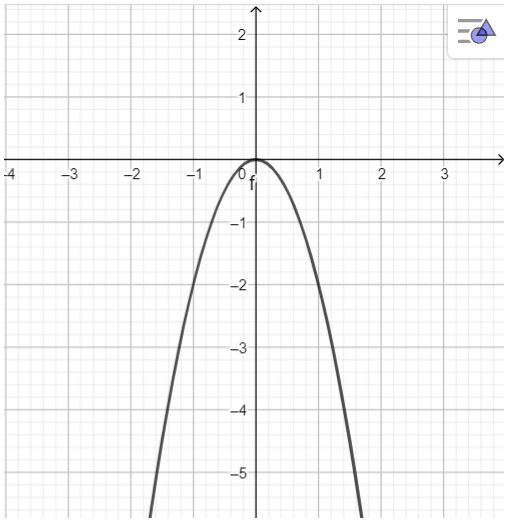
Hàm số đồng biến trên khoảng \((-\infty ;0)\) vì giá trị x tăng thì giá trị y tăng.
Hàm số nghịch biến trên khoảng \((0; +\infty)\) vì giá trị x tăng thì giá trị y giảm.
Câu 4: Giải các phương trình sau:
a) \(\sqrt{3x^{2}-6x+1}=\sqrt{-2x^{2}-9x+1}\)
b) \(\sqrt{3x^{2}-13x+14}= x-3\)
Hướng dẫn giải
a) \(\sqrt{3x^{2}-6x+1}=\sqrt{-2x^{2}-9x+1}\)
Bình phương hai vế của phương trình ta được”
\(3x^{2}-6x+1= -2x^{2}-9x+1\)
\(\Leftrightarrow \) \(5x^{2}+3x =0\)
\(\Leftrightarrow x=\frac{-3}{5}\) hoặc x=0
Thử lại các giá trị vào phương trình ban đầu ta thấy thỏa mãn.
Vậy phương trình đã cho có nghiệm là: \(x=\frac{-3}{5}\) hoặc x=0
b) \(\sqrt{3x^{2}-13x+14}= x-3\)
Bình phương hai vế của phương trình ta được:
\(3x^{2}-13x+14= x^{2}-6x+9\)
\(\Leftrightarrow\) \(x^{2}-7x+5=0\)
\(\Leftrightarrow x=1\) hoặc \(x=\frac{5}{2}\)
Thử lại các giá trị
- x = 1 không thỏa mãn phương trình.
- \(x = \frac{5}{2}\) không thỏa mãn phương trình.
Vậy phương trình vô nghiệm.
=============
– Học Toán lớp 10 – Kết nối
