Lý thuyết Bài 17: Dấu của tam thức bậc hai – Kết nối

Lý thuyết Bài 17: Dấu của tam thức bậc hai
=============

Tóm tắt lý thuyết

1.1. Dấu của tam thức bậc hai

Người ta thường viết f(x) = ax2 + bx + c. Các đa thức đã cho A = \(0,5x^{2}\), B = \(1-x^{2}\), C = \(x^{2}+x+1\), D = (1-x)(2x+1) là những tam thức bậc hai. Ở đa thức A, ta có ; a = 0,5; b = 0, c = 0.

Chú ý: Nghiệm của phương trình bậc hai ax2 + bx + c = 0 cũng được gọi là nghiệm của tam thức bậc hai ax2 + bx + c. 

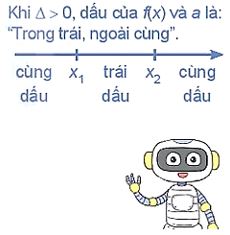
Chú ý: Trong Định lí về dấu tam thức bậc hai có thể thay \(\Delta \) bởi \(\Delta ‘\).

Ví dụ: Xét dâu các tam thức bậc hai sau:

\(\begin{array}{l}
a){x^2} + x + 1\\
b) – \frac{3}{2}{x^2} + 9x – \frac{{27}}{2}\\
c)2{x^2} + 6x – 8
\end{array}\)

Giải

a) \(f(x) = {x^2} + x + 1\) có \(\Delta = -3 < 0\) và a = 1 > 0 nên f(x) > 0 với mọi x \(\in\) R.

b) \(g(x) =  – \frac{3}{2}{x^2} + 9x – \frac{{27}}{2}\) có \(\Delta = 0\) và \(a =  – \frac{3}{2} > 0\) nên g(x) có nghiệm kép x = 3 và g(x) < 0 với mọi \(x \ne 3\).

c) Dễ thấy \(h(x) = 2{x^2} + 6x – 8\) có \(\Delta ‘ = 25 > 0,a = 2 > 0\) và có hai nghiệm phân biệt \({x_1} =  – 4;{x_2} = 1\).

Do đó ta có bẳng xét dấu h(x)

Suy ra h(x) > 0 với mọi \(x \in \left( { – \infty ; – 4} \right) \cup \left( {1; + \infty } \right)\) và h(x) < 0 với mọi \(x \in \left( { – 4;1} \right)\).

1.2. Bất phương trình bậc hai

Nhận xét: Để giải bất phương trình bậc hai ax2+ bx + c > 0 (hoặc \(a{x^2} + bx + c \ge 0\), ax2+ bx + c < 0, \(a{x^2} + bx + c \le 0\)) ta cần xét dấu tam thức ax2+ bx + c, từ đó suy ra tập nghiệm. 

Ví dụ: Giải các bất phương trình sau:

\(\begin{array}{l}
a)3{x^2} + x + 5 \le 0\\
b) – 3{x^2} + 2\sqrt 3  – 1 \ge 0\\
c) – {x^2} + 2x + 1 > 0
\end{array}\)

Giải

a) Tam thức \(f(x) = 3{x^2} + x + 5\) có \(\Delta  =  – 59 < 0\), hệ số a = 3 > 0 nên f(x) luôn dương (cùng dấu với a) với mọi x, tức là \(3{x^2} + x + 5 > 0\) với mọi \(x \in R\). Suy ra bất phường trình vô nghiệm.

b) Tam thức \(f(x) =  – 3{x^2} + 2\sqrt 3  – 1\) có \(\Delta ‘ = 0\), hệ số a = -3 < 0 nên f(x) luôn âm (cùng dấu với a) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\), tức là \(- 3{x^2} + 2\sqrt 3  – 1 < 0\) với mọi \(x = \frac{{\sqrt 3 }}{3}\).

Suy ra bất phương trình có nghiệm duy nhất \(x = \frac{{\sqrt 3 }}{3}\).

c) Tam thức \(f(x) =  – {x^2} + 2x + 1\) có \(\Delta ‘ = 2 > 0\) nên f(x) có hai nghiệm \({x_1} = 1 – \sqrt 2 \) và \({x_2} = 1 + \sqrt 2 \) 

Mặt khác a = -1 < 0, do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là \(S = \left( {1 – \sqrt 2 ;1 + \sqrt 2 } \right)\) 

Bài tập minh họa

Câu 1:  Cho hàm số bậc hai \(y=f(x)=x^{2}-4x+3\).

a) Xác định hệ số a. Tính f(0), f(1), f(2), f(3), f(4) và nhận xét về dấu của chúng so với dấu của hệ số a.

b) Cho đồ thị hàm số y = f(x) (H.6.17). Xét trên từng khoảng \((-\infty ;1),(1;3);(3;+\infty )\), đồ thị nằm phía trên hay nằm phía dưới trục Ox?

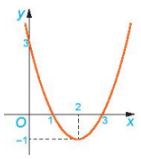
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.

Hướng dẫn giải

a) a = 1

\(f(0)=0^{2}-4.0+3=3\), cùng dấu với a

\(f(1)=1^{2}-4.1+3=0\), không mang dấu

\(f(2)=2^{2}-4.2+3=-1\), trái dấu với a

\(f(3)=3^{2}-4.3+3=0\), không mang dấu.

\(f(4)=4^{2}-4.4+3=3\), cùng dấu với a

b)

\((-\infty ;1)\): đồ thị nằm phía trên trục hoành.

(1; 3): đồ thị nằm phía dưới trục hoành.

\((3;+\infty )\): đồ thị nằm phía trên trục hoành.

c.

\((-\infty ;1)\): f(x) và hệ số a cùng dấu.

(1; 3): f(x) và hệ số a trái dấu.

\((3;+\infty )\): f(x) và hệ số a cùng dấu.

Câu 2:  Giải các bất phương trình bậc hai sau:

a) \(-5x^{2}+x-1\leq 0\)       

b) \(x^{2}-8x+16\leq 0 \)         

c) \(x^{2}-x+6> 0 \)

Hướng dẫn giải

a) Tam thức f(x) = \(-5x^{2}+x-1\) có \( \Delta = -19<0\), a = -5 < 0 nên f(x) luôn âm. Suy ra bất phương trình luôn đúng.

Vậy tập nghiệm bất phương trình là S = \(\mathbb{R}\)

b) Tam thức f(x) = \(x^{2}-8x+16\) có \(\Delta =0\) và a = 1 > 0 nên f(x) \(\geq >0\) với mọi \(x\in \mathbb{R}\).

Suy ra bất phương trình có nghiệm duy nhất x = 4.

c) Tam thức f(x) = \(x^{2}-x+6\) \(\Delta = -23<0\), a = 1 > 0 nên f(x) luôn dương. Suy ra bất phương trình luôn đúng.

Vậy tập nghiệm bất phương trình là S = \(\mathbb{R}\).

=============
– Học Toán lớp 10 – Kết nối