Lý thuyết Bài 15: Hàm số – Kết nối

Lý thuyết Bài 15: Hàm số
=============

Tóm tắt lý thuyết

1.1. Khái niệm hàm số

Nếu với mỗi giá tị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực R thì ta có một hàm số. Ta gọi x là biến số và y là hàm số của x. Tập hợp D gọi là tập xác định của hàm số. Tập tắt cả các giá trị y nhận được, gọi là tập giá trị của hàm số.

Ví dụ: Viết hàm số mô tả sự phụ thuộc của quãng đường đi được vảo thời gian của một vật chuyển động thẳng đều với vận tốc 2 m/s. Tìm tập xác định của hàm số đó. Tính quãng đường vật đi được sau 5s, 10s.

Giải

Một vật chuyển động thẳng đều với vận tốc v = 2 m/s thì quãng đường đi được S (mét) phụ thuộc vào thời gian t (giây) theo công thức S = 2t, trong đó t lả biến số, S = S(t) là hàm số của t.

Tập xác định của hàm số là Ð= [0; +).

Quảng đường vật đi được sau 5s là: S₁ = S(5) = 2.5 = 10 (m).

Quảng đường vật đi được sau 10s là: S₂ = S(10) = 2.10 = 20 (m).

Chú ý: Khi cho hàm số bằng công thức y= f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

1.2. Đồ thị của hàm số

Đồ thị hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng toạ độ với mọi x thuộc D.

Ví dụ:  Viết công thức của hàm số cho ở HĐ3b. Tìm tập xác định, tập giá trị và vẽ đồ thị của hàm số này.

Giải

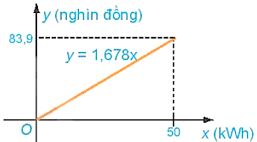
Công thức của hàm số cho ở HĐ3b là y = 1,678x với \(0 \le x \le 50\).

Tập xác định của hàm số này là D = [0: 50]

Vi \(0 \le x \le 50\) nên \(0 \le y \le 1,678.50 = 83,9\). 

Vậy tập giá trị của hàm số là [0; 83,9].

Đỏ thị của hàm số y = 1,678x trên [0; 50] là một đoạn thẳng.

1.3. Sự đồng biến, nghịch biến của hàm số

Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a; b), nếu \(\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).  Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu \(\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).

Ví dụ: Hàm số y = x² đồng biến hay nghịch biến trên mỗi khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\)?

Giải

Vẽ đồ thị hàm số y= f{x) = x² như hình sau:

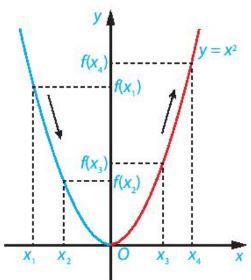
+ Trên khoảng \(\left( { – \infty ;0} \right)\), đồ thị “đi xuống” từ trái sang phải và với \({x_1},{x_2} \in \left( { – \infty ;0} \right)\), \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\). Như vậy hàm số y = x² nghịch biến trên khoảng \(\left( { – \infty ;0} \right)\). 

+ Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị “đi lên” từ trái sang phải và với \({x_3},{x_4} \in \left( {0; + \infty } \right)\), \({x_3} < {x_4}\) thì \(f\left( {{x_3}} \right) < f\left( {{x_4}} \right)\). Như vậy, hàm số y = x² đồng biến trên khoảng \(\left( {0; + \infty } \right)\). 

Chú ý

+ Đỗ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải;

+ Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường “đi xuống” từ trái sang phải.

Bài tập minh họa

Câu 1

a. Hãy cho biết Bảng sau có cho ta một hàm số hay không. Nếu có, tìm tập xác định và tập giá trị của hàm số đó.

b. Trở lại HD2, ta có hàm số cho bằng biểu đồ. Hãy cho biết giá trị của hàm số tại x = 2018. Tìm tập xác định, tập giá trị của hàm số đó.

c. Cho hàm số \(y=f(x)=-2x^{2}\). Tính f(1); f(2) và tìm tập xác định, tập giá trị của hàm số này.

Hướng dẫn giải

a. Bảng cho trên có cho ta một hàm số vì mỗi giá trị của x cho ta tương ứng một và chỉ một giá trị của y.

Tập xác định: D = {2013; 2014; 2015; 2016; 2017; 2018}

Tập giá trị: {73,1; 73,2; 73,3; 73,4; 73,5}

b. Giá trị hàm số tại x = 2018 là y = 242.

Tập xác định:  D = {2013; 2014; 2015; 2016; 2017; 2018; 2019}

Tập giá trị: {242; 241; 237; 239}.

c. f(1) = \(-2.1^{2}= -1\)

f(2) = \(-2.2^{2}=-8\)

Tập xác định: \(D=\mathbb{R}\)

Do \(x^{2}\geq 0, \forall x\in \mathbb{R}\) nên \(-2.x^{2}\leq 0, \forall x\in \mathbb{R}\)

Tập giá trị: \((-\infty ;0]\)

Câu 2:  Vẽ đồ thị của hàm số y = 3x + 1 và \(y = -2x^{2}\). Hãy cho biết:

a. Hàm số y = 3x + 1 đồng biến hay nghịch biến trên \(\mathbb{R}\).

b. Hàm số \(y =-2x^{2}\) đồng biến hay nghịch biến trên mỗi khoảng \((-\infty ;0)\) và \((0; +\infty)\).

Hướng dẫn giải

Đồ thị hàm số y = 3x + 1:

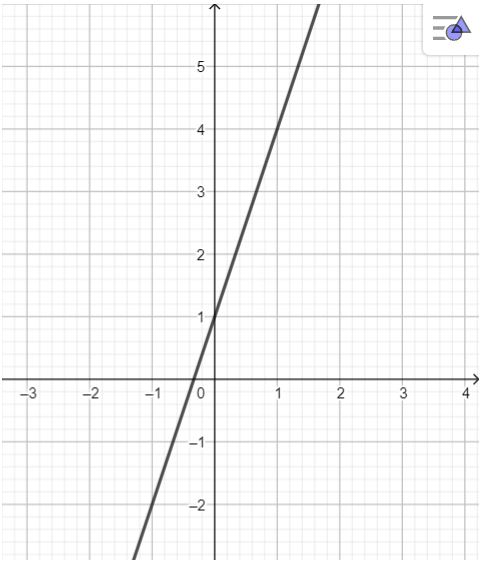
Hàm số đồng biến trên  \(\mathbb{R}\), vì giá trị của x tăng thì giá trị của y tăng.

b. Đồ thị hàm số  \(y =-2x^{2}\):

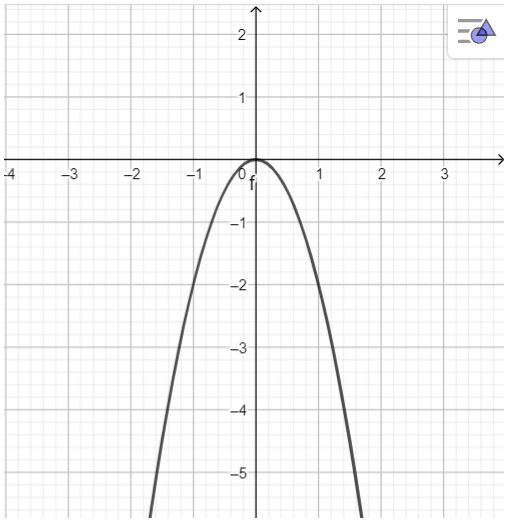
Hàm số đồng biến trên khoảng \((-\infty ;0)\) vì giá trị x tăng thì giá trị y tăng. 

Hàm số nghịch biến trên khoảng \((0; +\infty)\) vì giá trị x tăng thì giá trị y giảm. 

=============
– Học Toán lớp 10 – Kết nối