1. Định nghĩa
Hệ trục tọa độ gồm hai trục vuông góc \(Ox\) và \(Oy\) với hai vectơ đơn vị lần lượt là \(\overrightarrow i ,\,\overrightarrow j \). Điểm O gọi là gốc tọa độ, \(Ox\) gọi là trục hoành và \(Oy\) gọi là trục tung.
Kí hiệu \(Oxy\) hay \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\)
2. Tọa độ điểm, tọa độ vec tơ
+ Trong hệ trục tọa độ \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\) nếu \(\overrightarrow u = x\overrightarrow i + y\overrightarrow j \) thì cặp số \(\left( {x;y} \right)\) được gọi là tọa độ của vectơ \(\overrightarrow u \), kí hiệu là \(\overrightarrow u = \left( {x;y} \right)\) hay \(\overrightarrow u \left( {x;y} \right)\).
$x$ được gọi là hoành độ, $y$ được gọi là tung độ của vectơ \(\overrightarrow u \)
+ Nếu \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j \) thì \(\left( {x;y} \right)\) gọi là tọa độ của điểm $M$, kí hiệu là \(M = \left( {x;y} \right)\) hay \(M\left( {x;y} \right)\).
$x$ được gọi là hoành độ, $y$ được gọi là tung độ của điểm $M$ .

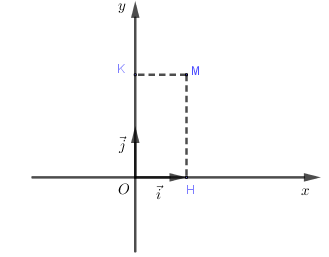
Gọi $H,K$ lần lượt là hình chiếu của $M$ lên \(Ox\) và \(Oy\) thì \(M\left( {x;y} \right) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j = \overrightarrow {OH} + \overrightarrow {OK} \)
Như vậy \(\overrightarrow {OH} = x\overrightarrow i ,\,\,\overrightarrow {OK} = y\overrightarrow j \) hay $x = \overline {OH} ,\,\,y = \overline {OK} $
3. Tọa độ trung điểm của đoạn thẳng. Tọa độ trọng tâm tam giác
Cho \(A({x_A};{y_A}),{\rm{ }}B({x_B};{y_B}),\,\,C\left( {{x_C};{y_C}} \right)\) phân biệt, không thẳng hàng và $M$ là trung điểm $AB$, \(G\) là trọng tâm của tam giác. Khi đó:
BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VÉC TƠ
+) ${x_M} = \dfrac{{{x_A} + {x_B}}}{2},$ ${y_M} = \dfrac{{{y_A} + {y_B}}}{2}$
+) ${x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}$ ${y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}$
Cho $\overrightarrow u = (x;y)$ ;$\overrightarrow {u’} = (x’;y’)$ và số thực $k$. Khi đó ta có:
1) \(\overrightarrow u = \overrightarrow {u’} \Leftrightarrow \left\{ \begin{array}{l}x = x’\\y = y’\end{array} \right.\)
2) $\overrightarrow u \pm \overrightarrow v = (x \pm x’;y \pm y’)$
3) $k.\overrightarrow u = (kx;ky)$
4) $\overrightarrow {u’} $ cùng phương $\overrightarrow u $($\overrightarrow u \ne \overrightarrow 0 $) khi và chỉ khi có số $k$ sao cho \(\left\{ \begin{array}{l}x’ = kx\\y’ = ky\end{array} \right.\)
+ Nếu \(k > 0\) thì \(\overrightarrow {u’} ,\overrightarrow u \) cùng hướng.
+ Nếu \(k < 0\) thì \(\overrightarrow {u’} ,\overrightarrow u \) ngược hướng.
5) Cho \(A({x_A};{y_A}),B({x_B};{y_B})\) thì:
+ \(\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A}} \right)\)
+ \(\left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} – {x_A}} \right)}^2} + {{\left( {{y_B} – {y_A}} \right)}^2}} \)
6) Tứ giác \(ABCD\) là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}{x_A} + {x_C} = {x_B} + {x_D}\\{y_A} + {y_C} = {y_B} + {y_D}\end{array} \right.\)
1. Bài tập cơ bản
Bài 1: Xác định tính đúng sai của các mệnh đề sau, nếu sai hãy giải thích
1. Hai vectơ \(\vec{a}(3;1)\) và vectơ \(\vec{b}(1;3)\) là hai vectơ bằng nhau.
2. Hai vectơ bằng nhau khi chúng có hoành độ và tung độ bằng nhau.
3. Vectơ \(\vec{a}\) cùng phương với vectơ \(\vec{b}\) nếu vectơ \(\vec{a}\) có tung độ bằng 0.
4. Hai vectơ cùng phương khi hoành độ của vectơ này bằng k lần hoành độ của vectơ kia, tung độ của vectơ này bằng -k lần tung độ vectơ kia.
Hướng dẫn:
Câu 1 là sai vì chúng chỉ có độ lớn bằng nhau, chứ hai vectơ không bằng nhau.
Câu 2 là câu đúng.
Câu 3 là câu sai, vì nếu cùng phương chúng sẽ tỉ lệ hoành và tung theo hệ số k nào đó.
Câu 4 là câu sai vì chúng tỉ lệ theo k hoặc -k chứ không phải hoành là k, tung là -k.
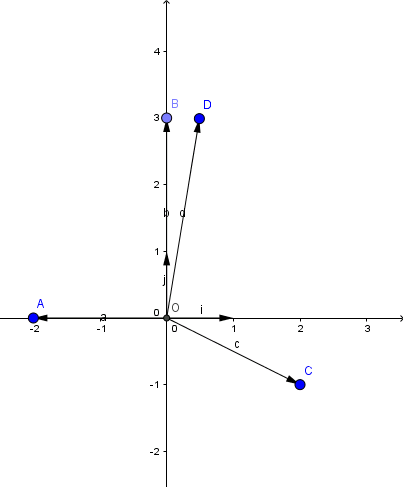
Bài 2: Biểu diễn các vectơ sau lên cùng một mặt phẳng tọa độ
\(\vec{a}=-2\vec{i}\), \(\vec{b}=3\vec{j}\), \(\vec{c}=2\vec{i}-\vec{j}\), \(\vec{d}=\frac{1}{2}\vec{i}+3\vec{j}\)
Hướng dẫn:
2. Bài tập nâng cao
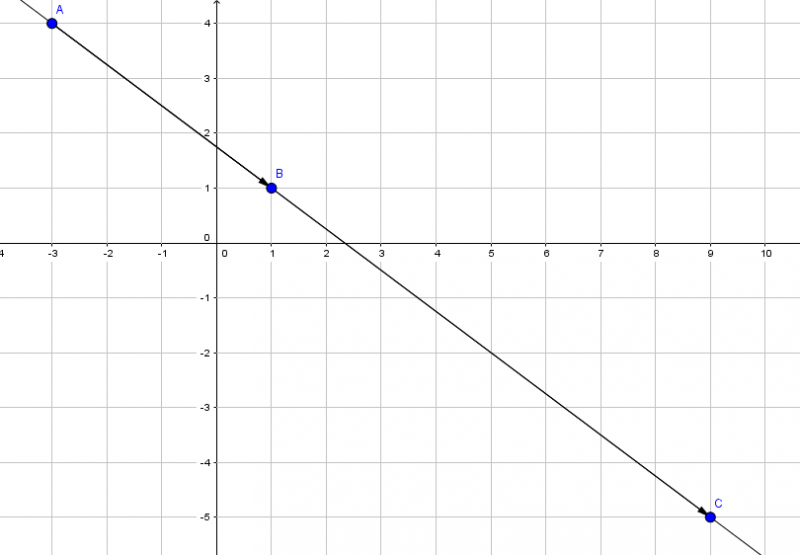
Bài 1: Chứng minh 3 điểm \(A(-3;4);B(1;1);C(9;-5)\) thẳng hàng
Hướng dẫn: Để chứng minh ba điểm này thẳng hàng, ta viết các vectơ \(\vec{AB};\vec{AC}\) rồi xác định hệ số k sao cho hoành và tung của \(\vec{AB}\) đúng bằng k lần hoành và tung của \(\vec{AC}\).
Thật vậy, \(\vec{AB}=(4;-3)\)
\(\vec{AC}=(12;-9)\)
Như vậy, hệ số k được xác định là \(k=3\). Vậy 3 điểm A, B, C thằng hàng.
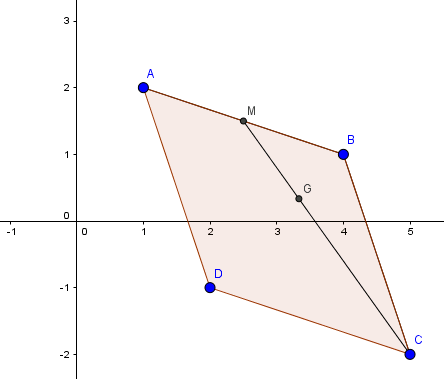
Bài 2: Trong mặt phẳng tọa độ. Cho 3 điểm \(A(1;2); B(4;1);C(5;-2)\).
1. Tìm tọa độ trung điểm M của AC.
2. Tìm tọa độ trọng tâm G của tam giác ABC.
3. Tìm tọa độ điểm D sao cho ABCD là hình bình hành.
Hướng dẫn:
1. Do M là trung điểm của AC nên \(x_M=\frac{x_A+x_C}{2},y_M=\frac{y_A+y_C}{2}\)
\(\Leftrightarrow x_M=\frac{1+5}{2},y_M=\frac{2+(-2)}{2}\)\(\Leftrightarrow x_M=3,y_M=0\Leftrightarrow M(3;0)\)
2. G là trọng tâm của tam giác ABC nên \(x_G=\frac{x_A+x_B+x_C}{3},y_M=\frac{y_A+y_B+y_C}{3}\)
\(\Leftrightarrow x_G=\frac{1+4+5}{3},y_G=\frac{2+1+(-2)}{3}\)\(\Leftrightarrow x_G=\frac{10}{3},y_G=\frac{1}{3}\Leftrightarrow G \left ( \frac{10}{3};\frac{1}{3} \right )\)
3. ABCD là hình bình hành, suy ra \(\vec{AB}=\vec{DC}\)
Mà \(\vec{AB}=(4-1;1-2)\Leftrightarrow \vec{AB}=(3;-1)\)
Suy ra \(\left\{\begin{matrix} x_D=5-3\\ y_D=-2-(-1) \end{matrix}\right.\)
Vậy \(D(2;-1)\)