Đề: Cho tứ diện ABCD có \(AB = 4a,CD = 6a,\) các cạnh còn lại đều bằng \(a\sqrt {22} \). Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD

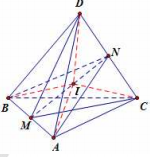
Gọi M, N là trung điểm của AB, CD.

Dễ dàng chứng minh (DMC) và (ANB) là lần lượt mặt phẳng trung trực của đoạn thẳng AB và CD \( \Rightarrow \) Tâm mặt cầu ngoại tiếp tứ diện ABCD là I nằm trên đường thẳng MN.

Tính được \(MN = \sqrt {D{M^2} – D{N^2}}  = \sqrt {D{B^2} – B{M^2} – D{N^2}}  = 3a\)

Đặt \(MI = x \ge 0 \Rightarrow \left\{ {\begin{array}{*{20}{c}}{B{I^2} = A{I^2} = B{M^2} + B{I^2} = 4{a^2} + {x^2}}\\{D{I^2} = C{I^2} = D{N^2} + I{N^2} = 9{a^2} + {{\left( {3a \pm x} \right)}^2}}\end{array}} \right.\)

\( \Leftrightarrow 4{a^2} + {x^2} = 9{a^2} + {\left( {3a \pm x} \right)^2} \Leftrightarrow x = \frac{{7a}}{3} \Rightarrow R = BI = \frac{{a\sqrt {85} }}{3}\)