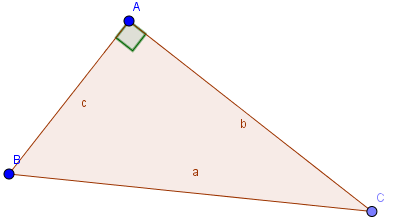
1. Định lí côsin trong tam giác
Xét tam giác ABC vuông tại A, ta có:

Ta đã biết rằng: \(BC^2=AB^2+AC^2\)
hay \(\vec {BC}^2=\vec {AB}^2+\vec {AC}^2\)
Chứng minh ngắn gọn theo tích vô hướng của hai vectơ ở bài học trước ta có được điều trên.
Như vậy, ta có phát biểu về định lí côsin trong tam giác:
Trong tam giác ABC, gọi \(Ab=c;AC=b;BC=a\), ta có:
\(a^2=b^2+c^2-2bc.cosA\)
\(b^2=a^2+c^2-2ac.cosB\)
\(c^2=a^2+b^2-2ab.cosC\)
Từ đó, ta có hệ quả sau:
\(cosA=\frac{b^2+c^2-a^2}{2bc}\)
\(cosB=\frac{a^2+c^2-b^2}{2ac}\)
\(cosC=\frac{a^2+b^2-c^2}{2ab}\)
2. Định lí sin trong tam giác
Cho hình vẽ:
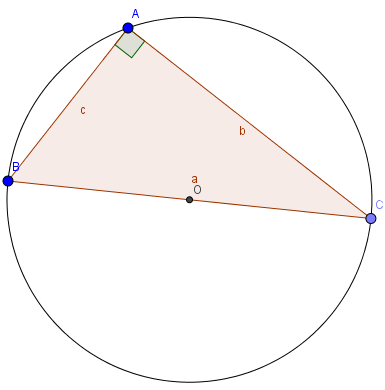
Ta dễ dàng nhận thấy rằng:
\(a=2RsinA, b=2RsinB, c=2RsinC\)
Chứng minh tương tự với tam giác thường, hệ thức trên vẫn đúng!
Ta rút ra được định lí sau:
Với mọi tam giác ABC, ta có:
\(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R\)
3. Tổng bình phương hai cạnh và độ dài đường trung tuyến của tam giác
Cho tam giác ABC có đường trung tuyến AM.
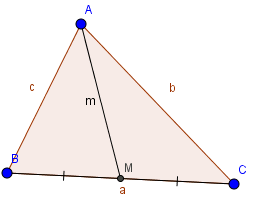
Gọi \(m_a;m_b;m_c\) lần lượt là các đường trung tuyến ứng với các cạnh a, b, c. Khi đó:
\(m_{a}^{2}=\frac{b^2+c^2}{2}-\frac{a^2}{4}\)
\(m_{b}^{2}=\frac{a^2+c^2}{2}-\frac{b^2}{4}\)
\(m_{c}^{2}=\frac{a^2+b^2}{2}-\frac{c^2}{4}\)
4. Diện tích tam giác
Ngoài kiến thức tính diện tích đã học ở cấp dưới là bằng nửa tích cạnh đáy nhân với chiều cao tương ứng, ta còn được biết thêm với các công thức sau:
Với tam giác ABC, kí hiệu \(h_a;h_b;h_c\) lần lượt là các đường cao ứng với các cạnh a, b, c. R, r là bán kính đường tròn ngoại tiếp và nội tiếp tam giác ABC, \(p=\frac{1}{2}(a+b+c)\) là nửa chu vi của tam giác, ta có các công thức tính diện tích S của tam giác ABC như sau:
\(S=\frac{1}{2}a.h_a=\frac{1}{2}b.h_b=\frac{1}{2}c.h_c\)
\(S=\frac{1}{2}ab.sinC=\frac{1}{2}ac.sinB=\frac{1}{2}bc.sinA\)
\(S=\frac{abc}{4R}\)
\(S=pr\)
\(S=\sqrt{p(p-a)(p-b)(p-c)}\)
5. Giải tam giác và ứng dụng thực tế
Giải tam giác là tính độ dài các cạnh và số đo các góc của tam giác dựa trên điều kiện cho trước.
Ví dụ: Cho hình vẽ sau:
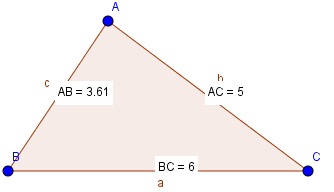
Hãy giải tam giác ABC.
Ta có:
\(a^2=b^2+c^2-2bc.cosA\)
\(\Leftrightarrow 6^2=5^2+3,61^2-2.5.3,61.cosA\)
\(\Leftrightarrow 36=25+13,03-36,1.cosA\)
\(\Rightarrow cosA=0,056\) \(\Rightarrow \widehat{A}\approx 86,77^o\)
Tương tự:
\(b^2=a^2+c^2-2ac.cosB\)
\(\Leftrightarrow 3,61^2=6^2+5^2-2.6.5.cosB\)
\(\Rightarrow cosB=0,779\) \(\Rightarrow \widehat{B}\approx 36,92^o\)
\(\Rightarrow \widehat{C}=180^o-\widehat{A}-\widehat{B}\approx 56,3^o\)
