Lý thuyết Bài tập cuối chương 9
=============
Tóm tắt lý thuyết
1.1. Biến cố và định nghĩa cổ điển của xác suất
a) Biến cố
+ Phép thử ngấu nhiên (gọi tắt là phép thử) là một thí nghiệm hay một hành động mà kết quả của nó không thể biết được trước khi phép thử được thực hiện.
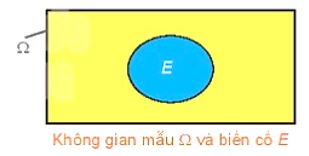
+ Không gian mẫu của phép thử là tập hợp tất cả các kết quả có thể khi thực hiện phép thử Không gian mẫu của phép thử được kí hiệu là \(\Omega \).
+ Kết quả thuận lợi cho một biến cố E liên quan tới phép thử T là kết quả của phép thử T làm cho biến cố đó xảy ra.
+ Mỗi biến cố là một tập con của không gian mẫu \(\Omega \). Tập con này là tập tất cae các kết quả thuận lợi cho biến cố đó.
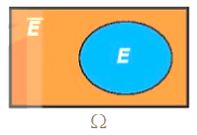
Biến cố đối của biến cố E là biến cố “E không xảy ra”. Biến cố đối của E được kí hiệu là \(\overline E \).
b) Định nghĩa cổ điển của xác suất
Cho phép thử T có không gian mẫu là \(\Omega \). Giả thiết rằng các kết quả có thể của T là đồng khả năng. Khi đó nếu E là một biến cổ liên quan đến phép thử T thì xác suất của E được cho bởi công thức
\(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}}\).
trong đỏ \({n\left( \Omega \right)}\) và \({n\left( E \right)}\) tương ứng là số phần tử của tập \(\Omega \) và tập E.
c) Nguyên lí xác suất bé
Qua thực tế người ta thấy rằng một biến cố có xác suất rất bé thì sẽ không xảy ra khi ta thực hiện một phép thử hay một vài phép thử. Từ đó người ta đã thừa nhận nguyên lí sau đây gọi là nguyên lí xác suất bé:
Nếu một biến có có xác suắt rất bé thì trong một phép thử biến cố đó sẽ không xảy ra.
1.2. Tính xác suất theo định nghĩa cổ điển
a) Sử dụng phương pháp tổ hợp
Trong nhiêu bài toán, để tính số phần từ của không gian mấu, của các biến cố, ta thường sử dụng các quy tắc đếm, các công thức tính số hoán vị, chỉnh hợp và tổ hợp.
b) Sử dụng sơ đồ hình cây
Trong một số bài toán, phép thử T được hinh thành tử một vài phép thừ, chẳng hạn: gieo xúc xắc liên tiếp bốn lần: lấy ba viên bi, mỗi viên từ một hộp;… Khi đó ta sử dụng sơ đồ hình cây để có thể mô tả đây đủ, trực quan không gian mẫu và biến có cần tính xác suất.
c) Xác suất của biến cố đối
Ta có công thức sau đây liên hệ giữa xác suất của một biển cố với xác suất của biến có đối.
Cho E là một biến cố. Xác suất của biến cố \(\overline E \) liên hệ với xác suất của E bởi công thức sau:
\(P\left( {\overline E } \right) = 1 – P\left( E \right)\)
Bài tập minh họa
Câu 1: Gieo đồng thời hai con xúc xắc cân đối. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 4 hoặc bằng 6.
Hướng dẫn giải
Vì mỗi con xúc xắc có thể xuất hiện 1 trong 6 mặt, nên số khả năng có thể xảy ra khi gieo 2 xúc xăc là: \(n(\Omega )=6^{2}=36\).
Biến cố E: ‘”Tổng số chấm xuất hiện trên hai con xúc xắc bằng 4 hoặc bằng 6″.
Tổng số chấm bằng 4 gồm các kết quả: (1; 3), (3; 1), (2; 2).
Tổng số chấm bằng 6 gồm các kết quả: (1; 5), (5; 1), (2; 4), (4; 2), (3; 3)
\(\Rightarrow\) Biến cố E có 8 phần tử, hay n(E) = 8.
Vậy P(E) = \(\frac{8}{36}=\frac{2}{9}\).
Câu 2: Môt tổ trong lớp 10B có 12 học sinh, trong đó có 7 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 6 học sinh trong tổ để kiếm tra vở bài tập Toán. Tính xác suất để trong 6 học sinh được chọn số học sinh nữ bằng số học sinh nam.
Hướng dẫn giải
Không gian mẫu: \(n(\Omega )=C_{12}^{6}\) = 924.
Biến cố A: “6 học sinh được chọn số học sinh nữ bằng số học sinh nam”.
Để số học sinh nữ băng số học sinh nam thì chọn 3 nữ và 3 nam.
\(\Rightarrow\) n(A) = \(C_{7}^{3}.C_{5}^{3}= 350\)
Vậy P(A) = \(\frac{350}{924}=\frac{25}{66}\).
Câu 3: Có ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2, số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.
a. Vẽ sơ đồ cây để mô tả các phần tử của không gian mẫu.
b. Gọi M là biến cố: “Trong ba thẻ rút ra có ít nhất một thẻ số 1”. Biến cố \(\overline{M}\) là tập con nào của không gian mẫu?
c. Tính P(M) và P(\(\overline{M}\)).
Hướng dẫn giải
a.
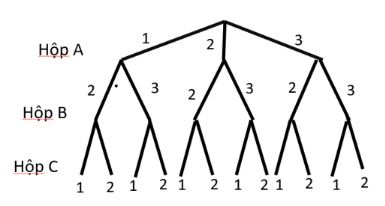
Vậy \(n(\Omega )\) = 12.
b. Biến cố \(\overline{M}\): “Trong ba thẻ rút ra không có thẻ số 1”.
\(\overline{M}\) = {222; 232; 322; 332}
c. P(\(\overline{M}\)) = \(\frac{4}{12}=\frac{1}{3}\)
P(M) = 1 – P(\(\overline{M}\)) = \(\frac{1}{3}\).
=============
– Học Toán lớp 10 – Kết nối

Để lại một bình luận