Lý thuyết Bài 2: Tập hợp. Các phép toán trên tập hợp – Toán 10 Cánh Diều
=======
1.1. Tập hợp
Ví dụ: Cho tập hợp B gồm các số tự nhiên có một chữ số và chi hết cho 3.
a) Viết tập hợp B theo hai cách: liệt kê các phần tử của tập hợp; chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
b) Minh hoạ tạp hợp B bằng biểu đồ ven.
Giải
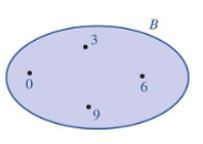
a) Tập hợp B được viết theo cách liệt kê các phần tử là: B = {0; 3; 6; 9}.
Tập hợp B được viết theo cách chỉ ra tính chất đặc trưng cho các phần tử là: \(B = {\rm{\{ }}x \in N|x \le 9\) và \(x \vdots 3\} \)
b) Tập hợp B được minh hoạ bằng biểu đồ Ven ở hình sau

Nhận xét
- Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng (tập rỗng), kí hiệu là \(\emptyset \).
- Một tập hợp có thể không có phần tử nào, cũng có thể có một phần tử, có nhiều phần tử, có vô số phần tử.
Chú ý: Khi tập hợp C là tập hợp rỗng, ta viết \(C = \emptyset \) và không được viết là \(C = \left\{ \emptyset \right\}\).
1.2. Tập con và tập hợp bằng nhau
a) Tập con
| Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập con của B và viết là \(A \subset B\). Ta còn đọc là A chứa trong B. |
|---|
Qui ước: Tập hợp rỗng \(\emptyset \) được coi là tập con của mọi tập hợp.
Chú ý: \(A \subset B \Leftrightarrow \left( {\forall x,x \in A \Rightarrow x \in B} \right).\)
Khi \(A \subset B\), ta cũng viết \(B \supset A\) (đọc là B chứa A)
Nếu A không phải là tập con của B, ta viết \(A \not\subset B\).
Ví dụ: Cho hai tập hợp: \(E = \left\{ {x \in R|x \le 1} \right\},F = \left\{ {x \in R|x < 2} \right\}\). Chứng tỏ rằng \(E \subset F\).
Giải
Lấy phần tử x tùy ý thuốc E. Ta có: \(x \le 1\). Vì \(x \le 1\) nên x < 2. Do đó \(x \in F\).
Vậy \(E \subset F\).
|
Ta có các tính chất sau:
|
|---|
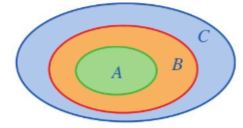
b) Tập hợp bằng nhau
| Khi \(A \subset B\) và \(B \subset A\) thì ta nói hai tập hợp A và B bằng nhau, viết là A = B. |
|---|
Chú ý: \(A = B \Leftrightarrow \left( {\forall x,x \in A \Leftrightarrow x \in B} \right)\).
Ví dụ: Cho C là tập hợp các tam giác có ba cạnh bằng nhau và D là tập hợp các tam giác có ba góc bằng nhau. Hai tập hợp C và D có bằng nhau hay không?
Giải
Do một tam giác có ba cạnh bằng nhau khi và chỉ khi tam giác đó có ba góc bằng nhau nên hai tập hợp C và D là bằng nhau.
1.3. Giao của hai tập hợp
| Tập hợp gồm tất cả các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B được gọi là giao của hai tập hợp A và B, kí hiệu \(A \cap B\). |
|---|
Vậy \(A \cap B = {\rm{\{ x|x}} \in {\rm{A}}\) và \(x \in {\rm{B\} }}\)
Tập hợp \(A \cap B\) được minh họa bởi phần gạch chéo trong hình sau
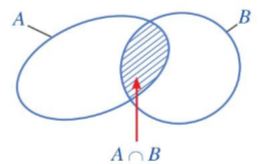
Lưu ý: \(x \in A \cap B\) khi và chỉ khi \(x \in A\) và \(x \in B\)
Ví dụ: Tìm giao của hai tập hợp trong mỗi trường hợp sau:
a) A = {x \(\in\) N | x là ước của 16}, B = {x \(\in\) N | x là ước của 20}
b) C = {x \(\in\) N | x là bội của 4}, D = {x \(\in\) N | x là bội của 5}
Giải
a) A = {1; 2; 4; 8; 16}, B = {1; 2; 4; 5; 10; 20}. Vậy \(A \cap B = \left\{ {1;2;4} \right\}\)
Chú ý: A là tập hợp các ước tự nhiên của 16, B là tâp hợp các ước tự nhiên của 20 nên \(A \cap B\) là tập hợp các ước chung tự nhiên của 16 và 20.
b) \(C \cap D\) = {x \(\in\) N | x là bội của 4 và x là bội của 5}
= {x \(\in\) N | x là bội chung của 4 và 5}
1.4. Hợp của hai tập hợp
| Tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B được gọi là hợp của hai tập hợp A và B, kí hiệu \(A \cup B\) |
|---|
Vậy \(A \cup B\) = {x | x \(\in\) A hoặc x \(\in\) B}.
Tập hợp \(A \cup B\) được minh họa bởi phần gạch chéo trong hình sau
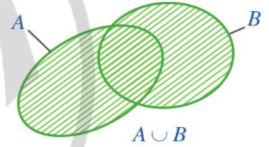
Lưu ý: \(x \in A \cup B\) khi và chỉ khi \(x \in A\) hoặc \(x \in B\)
Ví dụ: Cho tập hợp Q các số hữu tỉ và tập hợp I các số vô tỉ. Tìm \(Q \cap I,Q \cup I\)
Giải
Ta có: \(Q \cap I = \emptyset ,Q \cup I = R\)
1.5. Phần bù. Hiệu của hai tập hợp
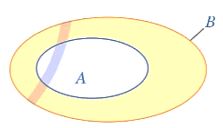
– Cho tập hợp A là tập con của tập hợp B. Tập hợp những phần tử thuộc B mà không thuộc A được gọi là phần bù của A trong B, kí hiệu \({C_B}A\)
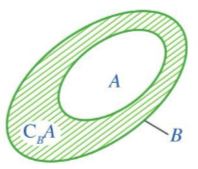
– Tập hợp gồm các phần tử thuộc A nhưng không thuộc B được gọi là hiệu của A và B, kí hiệu A\B.
Vậy \(A\backslash B\) = {x | x \(\in\) A và x \(\notin\) B}.
Tập hợp \(A\backslash B\) được minh họa bởi phần gạch chéo trong hình sau
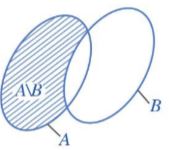
Ví dụ: Tìm \(A \cap B,A \cup B,A\backslash B,B\backslash A\).
Giải
Ta có: \(A = \left\{ {0;1;2;3} \right\},B = \left\{ 1 \right\}\)
Vậy \(A \cap B = \left\{ 1 \right\},A \cup B = \left\{ {0;1;2;3} \right\},A\backslash B = \left\{ {0;2;3} \right\},B\backslash A = \emptyset \)
1.6. Các tập hợp số
a) Các tập hợp số đã học
Ta đã biết N, Z, Q, R lần lượt là tập hợp số tự nhiên, tập hợp số nguyên, tập hợp số hữu tỉ, tập hợp số thực.
Ta có quan hệ sau: \(N \subset Z \subset Q \subset R\)
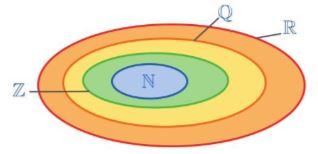
b) Một số tập con thường dùng của tập hợp số thực
Cho a và b là hai số thực với a < b.
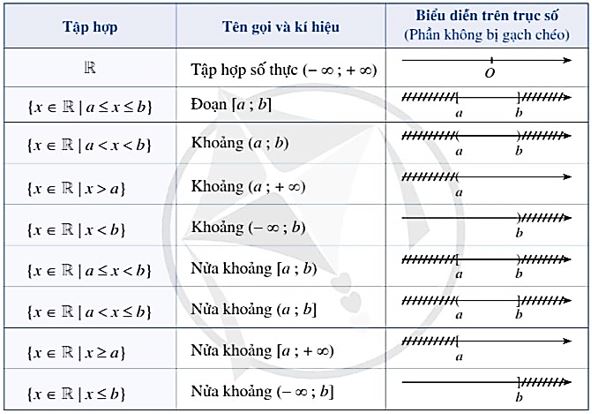
Kí hiệu \( – \infty \) đọc là âm vô cực, kí hiệu \( + \infty \) đọc là dương vô cực; a và b được gọi là đầu mút của các đoạn, khoảng, nửa khoảng.
Chú ý: Ta có thể biểu diễn tập hợp trên trục số bằng cách tô màu phần thuộc tập đó, chẳng hạn đoạn [a; b] có thể biểu diễn ở phần tô màu đỏ như hình sau:
![]()
Câu 1: Nêu số phần tử của mỗi tập hợp sau:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} ,\) \(D = \{ a\} ,E = \{ b;c;d\} ,\)\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\)
Hướng dẫn giải
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} \). Tập hợp C không chứa phần tử nào vì bình phương mọi số thực đều không âm.
\(D = \{ a\} ,\) tập hợp D có duy nhất 1 phần tử là a.
\(E = \{ b;c;d\} ,\) tập hợp E có 3 phần tử.
\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\): tập hợp N có vô số phần tử.
Câu 2: Cho hai tập hợp:
\(A = \{ n \in N|n\)chia hết cho 3},
\(B = \{ n \in N|n\)chia hết cho 9}.
Chứng tỏ rằng \(B \subset A.\)
Hướng dẫn giải
Lấy n bất kì thuộc tập hợp B.
Ta có: n chia hết cho 9 \( \Rightarrow n = 9k\;\;(k \in \mathbb{N})\)
\( \Rightarrow n = 3.(3k)\;\; \vdots \;3\;\;(k \in \mathbb{N})\)
\( \Rightarrow n \in A\)
Như vậy, mọi phần tử của tập hợp B đều là phần tử của tập hợp A hay \(B \subset A.\)
Câu 3: Cho hai tập hợp:
\(A = \left\{ {x \in \mathbb{Z}| – 2 \le x \le 3} \right\}\)
\(B = \{ x \in \mathbb{R}|{x^2} – x – 6 = 0\} \)
Tìm \(A\,{\rm{\backslash }}\,B\) và \(B\,{\rm{\backslash }}\,A\).
Hướng dẫn giải
Ta có: \(A = \left\{ {x \in \mathbb{Z}| – 2 \le x \le 3} \right\} = \{ – 2; – 1;0;1;2;3\} \)
Và \(B = \{ x \in \mathbb{R}|{x^2} – x – 6 = 0\} = \{ – 2;3\} \)
Khi đó:
Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các phần tử thuộc A mà không thuộc B. Vậy\(A\,{\rm{\backslash }}\,B = \{ – 1;0;1;2\} \).
Tập hợp \(B\,{\rm{\backslash }}\,A\) gồm các phần tử thuộc B mà không thuộc A. Vậy \(B\,{\rm{\backslash }}\,A = \emptyset \)
============
Thuộc chủ đề: Học Toán lớp 10 – Cánh diều
