Giải SBT Bài CUỐI Chương 8 – SBT Toán 10 KNTT

GIẢI CHI TIẾT Giải SBT Bài CUỐI Chương 8 – SBT Toán 10 KNTT
============

Giải bài 8.18 trang 58 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng quy tắc nhân.

Lời giải chi tiết

–  Từ Hà Nội tới Hải Phòng có 5 cách chọn xe

–  Để quay lại Hà Nội bằng một xe khác thì có 5-1=4 cách.

Theo quy tắc nhân thì có số cách đi là: 5. 4= 20

Chọn D

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.19 trang 58 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng quy tắc nhân.

Lời giải chi tiết

–  Chọn chữ số hàng đơn vị có 4 cách (2, 4, 6, 8) do số đó là số chẵn.

Vì các chữ số đôi một khác nhau nên:

–  Chọn chữ số hàng chục có 8 cách (khác chữ số hàng đơn vị)

–  Chọn chữ số hàng trăm có 7 cách (khác chữ số hàng đơn vị và hàng trục)

 Theo quy tắc nhân, số các số tự nhiên thỏa mãn yêu cầu là: 4. 7. 8= 224 số

Chọn A

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.20 trang 58 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Các số tự nhiên trong khoảng từ 3 000 đến 4 000, chia hết cho 5 thì có chữ số hàng nghìn là 3 và chữ số hàng đơn vị là 5.

Lời giải chi tiết

Số cần tìm có dạng \(\overline {3ab5} \), với \(a,b\) khác nhau và \(a,b\) chọn trong các chữ số 1; 2; 4; 6

Khi đó số bộ hai số khác nhau, có sắp thứ tự, lấy ra từ 4 số đó là: \(A_4^2\)

Chọn B 

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.21 trang 58 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng công thức tổ hợp \(C_n^k = \frac{{n!}}{{k!\left( {n – k} \right)!}} = \frac{{n.(n – 1)…(n – k + 1)}}{{k!}}\)

Lời giải chi tiết

Mỗi tam giác được xác định bởi ba điểm đánh dấu nên số tam giác với n điểm được đánh dấu là \(C_n^3\).

 Tương tự số tứ giác với n điểm được đánh dấu là \(C_n^4\)

 Số tam giác bằng số tứ giác nên ta có: \(\begin{array}{l}C_n^3 = C_n^4 \Leftrightarrow \frac{{n.(n – 1).(n – 2)}}{{3!}} = \frac{{n.(n – 1).(n – 2).(n – 3)}}{{4!}}\\ \Leftrightarrow 1 = \frac{{n – 3}}{4}\\ \Leftrightarrow n = 7\end{array}\)

Chọn C.

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.22 trang 58 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng quy tắc nhân.

Lời giải chi tiết

Mỗi thành viên có 3 cách bầu khác nhau và số thành viên hội đồng là 5 nên có số cách bầu là \(3.3.3.3.3 = {3^5}\)

Chọn C. 

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.23 trang 58 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng công thức hoán vị và quy tắc cộng.

Lời giải chi tiết

 Gọi thứ tự các bài báo cáo là 1, 2, 3, 4, 5. Có 4 phương án sắp xếp báo cáo của đại diện lớp 10B ngay sau báo cáo đại diện của 10A là:

– 10A báo cáo 1, 10B báo cáo 2

– 10A báo cáo 2, 10B báo cáo 3

– 10A báo cáo 3, 10B báo cáo 4

– 10A báo cáo 4, 10B báo cáo 5

Với mỗi phương án ta sắp xếp thứ tự đại diện của 10C, 10D, 10E theo thứ tự bất kì vào vị trí các báo cáo còn lại.

Do đó với mỗi phương án thì số cách sắp xếp là: 3!= 6 cách

Theo quy tắc cộng, số cách sắp xếp chương trình là:

6+ 6+ 6+ 6= 24 cách

Chọn A

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.24 trang 58 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng công thức tổ hợp.

Lời giải chi tiết

 Vì chỉ có 4 đại biểu nữ nên ta có 2 trường hợp.

– Trường hợp 1: Ủy ban gồm 3 nữ và 3 nam.

Số cách chọn ra 3 người từ 4 đại biểu nữ là: \(C_4^3 = 4\)cách

Số cách chọn ra 3 người từ 6 đại biểu nam là: \(C_6^3 = 20\)cách

– Trường hợp 2: Ủy ban gồm 4 nữ và 2 nam.

Số cách chọn ra 4 người từ 4 đại biểu nữ là: 1 cách

Số cách chọn ra 2 người từ 6 đại biểu nam là: \(C_6^2 = 15\) cách

Vậy có số cách thành lập ủy ban là:

4. 20 + 1. 15= 95 cách

Chọn D.

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.25 trang 59 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

 Áp dụng công thức hoán vị và quy tắc nhân.

Lời giải chi tiết

Xét 1 cặp vợ chồng là 1 nhóm. Số cách xếp 3 nhóm vào 3 vị trí là:

3!= 6 cách

 Với mỗi cách xếp như trên mỗi cặp vợ chồng có thể đổi chỗ cho nhau để tạo ra cách xếp mới.

 Tổng số cách xếp chỗ theo yêu cầu đề bài là:

6. 2. 2. 2= 48 cách

Chọn C.

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.26 trang 59 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng công thức khai triển \({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)

Lời giải chi tiết

Ta có:

\(\begin{array}{l}{(1 + x)^4} = {1^4} + {4.1^3}.x + {6.1^2}.{x^2} + 4.1.{x^3} + {x^4}\\\quad \quad \quad  = 1 + 4x + 6{x^2} + 4{x^3} + {x^4}\end{array}\)

Tổng các hệ số trong khai triển là: 1 +4 +6 + 4 + 1= 16

Chọn D. 

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.27 trang 59 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

 Áp dụng công thức khai triển\({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\).

Lời giải chi tiết

Ta có: \({\left( {\sqrt 5  + 1} \right)^5} – {\left( {\sqrt 5  – 1} \right)^5}\)

\(\begin{array}{l} = \left[ {{{\left( {\sqrt 5 } \right)}^5} + 5{{\left( {\sqrt 5 } \right)}^4} + 10{{\left( {\sqrt 5 } \right)}^3} + 10{{\left( {\sqrt 5 } \right)}^2} + 5.\sqrt 5  + {1^5}} \right]\\ – \left[ {{{\left( {\sqrt 5 } \right)}^5} + 5{{\left( {\sqrt 5 } \right)}^4}.( – 1) + 10{{\left( {\sqrt 5 } \right)}^3}{{( – 1)}^2} + 10{{\left( {\sqrt 5 } \right)}^2}{{( – 1)}^3} + 5.\sqrt 5 .{{( – 1)}^4} + {{( – 1)}^5}} \right]\\ = \left[ {{{\left( {\sqrt 5 } \right)}^5} + 5{{\left( {\sqrt 5 } \right)}^4} + 10{{\left( {\sqrt 5 } \right)}^3} + 10{{\left( {\sqrt 5 } \right)}^2} + 5.\sqrt 5  + {1^5}} \right]\\ – \left[ {{{\left( {\sqrt 5 } \right)}^5} – 5{{\left( {\sqrt 5 } \right)}^4} + 10{{\left( {\sqrt 5 } \right)}^3} – 10{{\left( {\sqrt 5 } \right)}^2} + 5.\sqrt 5  – {1^5}} \right]\\ = {\left( {\sqrt 5 } \right)^5} + 5{\left( {\sqrt 5 } \right)^4} + 10{\left( {\sqrt 5 } \right)^3} + 10{\left( {\sqrt 5 } \right)^2} + 5.\sqrt 5  + {1^5}\\ – {\left( {\sqrt 5 } \right)^5} + 5{\left( {\sqrt 5 } \right)^4} – 10{\left( {\sqrt 5 } \right)^3} + 10{\left( {\sqrt 5 } \right)^2} – 5.\sqrt 5  + {1^5}\\ = 10{\left( {\sqrt 5 } \right)^4} + 20{\left( {\sqrt 5 } \right)^2} + 2\\ = 10.25 + 20.5 + 2\\ = 352\end{array}\)

Chọn B.

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.28 trang 59 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

 Áp dụng quy tắc nhân, công thức hoán vị, chỉnh hợp

Lời giải chi tiết

Có tất cả 5+3=8 bạn học sinh.

–  Chọn ra 2 bạn nam đứng ngoài cùng bên trái và đứng ngoài cùng bên phải có số cách là: \(A_5^2 = 20\) cách

–   Xếp 6 bạn còn lại vào các vị trí giữa 2 bạn nam có 6!= 720 cách

Theo quy tắc nhân, tổng số cách sắp xếp là:

20. 720 = 14 400 cách

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.29 trang 59 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng quy tắc cộng, quy tắc nhân và công thức hoán vị.

Lời giải chi tiết

Đánh số các hàng từ trên xuống dưới lần lượt là 1, 2, 3, 4 ta có 2 phương án:

–  Phương án 1: Xếp các thí sinh nam vào hàng 1 và 3, còn các thí sinh nữ vào hàng 2, 4.

Xếp 10 thí sinh nam vào 10 chỗ ở hàng 1 và 3 có số cách là:

10!= 3 628 800 cách

Xếp 10 thí sinh nữ vào 10 chỗ ở hàng 2 và 4 có số cách là:

10!= 3 628 800 cách

Có tổng số cách sắp xếp theo phương án 1 là:

10!. 10! cách

–  Phương án 2: Xếp các thí sinh nam vào hàng 2 và 4, còn các thí sinh nữ vào hàng 1, 3.

Tương tự phương án 1, phương án 2 có 10!. 10! cách

Theo quy tắc cộng, số cách sắp xếp theo yêu cầu là:

10!. 10!+ 10!. 10!= 26 336 378 880 000 cách

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.30 trang 59 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

 Áp dụng quy tắc nhân, công thức hoán vị, chỉnh hợp

Lời giải chi tiết

–  Ta cần nhốt 5 con vật lớn nhất vào 5 trong 7 cái chuồng phù hợp có số cách là: \(A_7^5 = 2520\)

–  Số cách nhốt 5 con vật còn lại vào 5 chuồng còn lại là:

 5!= 120 cách

Theo quy tắc nhân, số cách nhốt theo yêu cầu là: 2 520. 120= 302 400 cách

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.31 trang 59 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng quy tắc cộng, quy tắc nhân và công côngthuwcs hoán vị.

Lời giải chi tiết

a)    Ta đánh số các chiếc ghế từ trái qua phải 1, 2, 3, 4, 5, 6

Để xếp các bạn nam và các bạn nữ ngồi xen kẽ nhau ta có:

–  Phương án 1: các bạn nữ ngồi ghế 1, 3, 5 và các bạn nam ngồi ghế 2, 4, 6

–  Phương án 2: các bạn nữ ngồi ghế  2, 4, 6 và các bạn nam ngồi ghế 1, 3, 5

Số cách xếp 3 bạn nữ vào 3 chỗ ngồi là 3!= 6 cách

Số cách xếp 3 bạn nam vào 3 chỗ ngồi còn lại là 3!= 6 cách

Số cách sắp xếp chỗ ngồi của mỗi phương án là: 6. 6= 36 cách

Vậy có tổng cách xếp chỗ ngồi theo yêu cầu là:  36+ 36= 72 cách

a)    Để xếp chỗ cho các bạn nữ ngồi liên tiếp nhau ta có:

–   Phương án 1: các bạn nữ ngồi ghế 1, 2, 3

–  Phương án 2: các bạn nữ ngồi ghế 2, 3, 4

–   Phương án 3: các bạn nữ ngồi ghế 3, 4, 5

–   Phương án 4: các bạn nữ ngồi ghế 4, 5, 6

Tương tự như câu a số cách xếp chỗ ngồi cho 3 bạn nữ vào 3 chỗ và số cách xếp chỗ ngồi cho 3 bạn nam đều bằng 6.

Do đó số cách sắp xếp chỗ ngồi của mỗi phương án là: 6. 6= 36 cách.

Vậy có tổng số cách sắp xếp chỗ theo yêu cầu là: 36+ 36+ 36+ 36= 144 cách

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.32 trang 59 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng công thức tổ hợp \(C_n^k = \frac{{n!}}{{k!\left( {n – k} \right)!}} = \frac{{n.(n – 1)…(n – k + 1)}}{{k!}}\)

Lời giải chi tiết

Gọi số người của nhóm bạn là n  \((n \in \mathbb{N}*)\)

 Số các cặp song ca là số cách chọn ra 2 người từ n người:

\(C_n^2 = \frac{{n!}}{{2!\left( {n – 2} \right)!}} = \frac{{n.(n – 1)}}{2}\)

Mỗi cặp song ca mất 2 phút nên tổng thời gian hát là:

\(2.\frac{{n.(n – 1)}}{2} = n.(n – 1) = 30\) (phút)

\(\begin{array}{l} \Leftrightarrow {n^2} – n – 30 = 0\\ \Leftrightarrow \left[ \begin{array}{l}n = 6\\n =  – 5\;(L)\end{array} \right.\\ \Rightarrow n = 6\end{array}\)

 Vậy nhóm bạn có 6 người.

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.33 trang 60 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

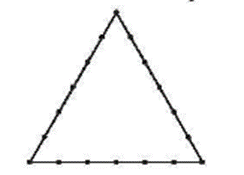
Phương pháp giải

 Áp dụng công thức tổ hợp và quy tắc cộng.

Lời giải chi tiết

 Tổng số chấm điểm trong hình là 18.

 Mỗi tam giác được tạo thành từ 3 điểm không thẳng hàng. Ta tính số cách chọn ra 3 điểm không thẳng hàng bằng số cách lấy số cách chọn ra 3 điểm trừ đi cách chọn ra 3 điểm thẳng hàng.

 Số cách chọn ra 3 điểm từ 18 điểm là:

\(C_{18}^3 = 816\) cách

Chọn ra 3 điểm thẳng hàng bằng cách chọn ra 3 điểm trên cùng 1 cạnh.

Mỗi cạnh có 7 điểm do đó có số cách chọn ra 3 điểm từ 1 cạnh là \(C_7^3 = 35\)cách

Số cách chọn ra 3 điểm thẳng hàng là 35+ 35+ 35= 105 cách

Vậy số tam giác cần tìm là: 816 – 105= 711.

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.34 trang 60 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng công thức tổ hợp và quy tắc nhân.

Lời giải chi tiết

Mỗi hình chữ nhật được tạo thành từ giao điểm của 2 đường thẳng của họ các đường đường thẳng nằm ngang và 2 đường thẳng của họ các đường thẳng nằm dọc.

 Số cách chọn ra 2 đường thẳng từ 6 đường thẳng nằm ngang là: \(C_6^2 = 15\)cách

Số cách chọn ra 2 đường thẳng từ 6 đường thẳng nằm dọc là: \(C_6^2 = 15\) cách

 Theo quy tắc nhân, số hình chữ nhật được tạo thành là: 15. 15= 225 cách 

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.35 trang 60 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

 Áp dụng quy tắc nhân, công thức hoán vị và chỉnh hợp.

Lời giải chi tiết

a) Từ “NGHI” có 4 chữ cái khác nhau.

Số cách sắp xếp theo yêu cầu là: 4!= 24 cách

b) Từ “NGHIÊN” có 6 chữ cái trong đó có 2 chữ cái N giống nhau.

Chọn  2 vị trí trong 6 vị trí để xếp 2 chữ N vào có \(C_6^2 = 15\)cách

Xếp 4 chữ cái còn lại vào vị trí còn lại có 4!= 24 cách

Số dãy kí tự tạo thành theo yêu cầu là 15. 24= 360 cách

c) Tương tự như câu b) từ “NGHIÊNG” có 7 chữ cái trong đó có các chữ cái giống nhau là N và G.

Để xếp 7 chữ cái thành 1 dãy kí tự  ta thực hiện lần lượt:

– Chọn 2 vị trí trí trong 7 vị trí để xếp 2 chữ N vào có \(C_7^2 = 21\) cách

– Chọn 2 vị trí trí trong 5 vị trí để xếp 2 chữ G vào có \(C_5^2 = 10\)cách

–  Xếp 3 chữ cái còn lại vào 3 vị trí còn lại có 3!= 6 cách

Số dãy kí tự được tạo thành theo yêu cầu là: 21. 10. 6= 1 260 cách.

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.36 trang 60 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng công thức khai triển \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\).

Lời giải chi tiết

Ta có: \({\left( {\sqrt 3  + \sqrt 2 } \right)^5} – {\left( {\sqrt 3  – \sqrt 2 } \right)^5}\)

\(\begin{array}{l} = {\left( {\sqrt 3 } \right)^5} + 5{\left( {\sqrt 3 } \right)^4}\left( {\sqrt 2 } \right) + 10{\left( {\sqrt 3 } \right)^3}{\left( {\sqrt 2 } \right)^2} + 10{\left( {\sqrt 3 } \right)^2}{\left( {\sqrt 2 } \right)^3} + 5.\left( {\sqrt 3 } \right){\left( {\sqrt 2 } \right)^4} + {\left( {\sqrt 2 } \right)^5}\\ – \left[ {{{\left( {\sqrt 3 } \right)}^5} + 5{{\left( {\sqrt 3 } \right)}^4}\left( { – \sqrt 2 } \right) + 10{{\left( {\sqrt 3 } \right)}^3}{{\left( { – \sqrt 2 } \right)}^2} + 10{{\left( {\sqrt 3 } \right)}^2}{{\left( { – \sqrt 2 } \right)}^3} + 5.\left( {\sqrt 3 } \right){{\left( { – \sqrt 2 } \right)}^4} + {{\left( { – \sqrt 2 } \right)}^5}} \right]\\ = {\left( {\sqrt 3 } \right)^5} + 5{\left( {\sqrt 3 } \right)^4}\left( {\sqrt 2 } \right) + 10{\left( {\sqrt 3 } \right)^3}{\left( {\sqrt 2 } \right)^2} + 10{\left( {\sqrt 3 } \right)^2}{\left( {\sqrt 2 } \right)^3} + 5.\left( {\sqrt 3 } \right){\left( {\sqrt 2 } \right)^4} + {\left( {\sqrt 2 } \right)^5}\\ – \left[ {{{\left( {\sqrt 3 } \right)}^5} – 5{{\left( {\sqrt 3 } \right)}^4}\left( {\sqrt 2 } \right) + 10{{\left( {\sqrt 3 } \right)}^3}{{\left( {\sqrt 2 } \right)}^2} – 10{{\left( {\sqrt 3 } \right)}^2}{{\left( {\sqrt 2 } \right)}^3} + 5.\left( {\sqrt 3 } \right){{\left( {\sqrt 2 } \right)}^4} – {{\left( {\sqrt 2 } \right)}^5}} \right]\\ = {\left( {\sqrt 3 } \right)^5} + 5{\left( {\sqrt 3 } \right)^4}\left( {\sqrt 2 } \right) + 10{\left( {\sqrt 3 } \right)^3}{\left( {\sqrt 2 } \right)^2} + 10{\left( {\sqrt 3 } \right)^2}{\left( {\sqrt 2 } \right)^3} + 5.\left( {\sqrt 3 } \right){\left( {\sqrt 2 } \right)^4} + {\left( {\sqrt 2 } \right)^5}\\ – {\left( {\sqrt 3 } \right)^5} + 5{\left( {\sqrt 3 } \right)^4}\left( {\sqrt 2 } \right) – 10{\left( {\sqrt 3 } \right)^3}{\left( {\sqrt 2 } \right)^2} + 10{\left( {\sqrt 3 } \right)^2}{\left( {\sqrt 2 } \right)^3} – 5.\left( {\sqrt 3 } \right){\left( {\sqrt 2 } \right)^4} + {\left( {\sqrt 2 } \right)^5}\\ = 10{\left( {\sqrt 3 } \right)^4}\left( {\sqrt 2 } \right) + 20{\left( {\sqrt 3 } \right)^2}{\left( {\sqrt 2 } \right)^3} + 2{\left( {\sqrt 2 } \right)^5}\\ = 10.9.\sqrt 2  + 20.3.2.\sqrt 2  + 2.4.\sqrt 2 \\ = 218\sqrt 2 \end{array}\) 

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

Giải bài 8.37 trang 60 SBT Toán 10 Kết nối tri thức tập 2 – KNTT

Phương pháp giải

Áp dụng công thức khai triển \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\).

Lời giải chi tiết

Ta có:

\(\begin{array}{l}{\left( {{x^2} + \frac{r}{x}} \right)^5} = {\left( {{x^2}} \right)^5} + 5{\left( {{x^2}} \right)^4}\frac{r}{x} + 10{\left( {{x^2}} \right)^3}{\left( {\frac{r}{x}} \right)^2} + 10{\left( {{x^2}} \right)^2}{\left( {\frac{r}{x}} \right)^3} + 5\left( {{x^2}} \right){\left( {\frac{r}{x}} \right)^4} + {\left( {\frac{r}{x}} \right)^5}\\ = {x^{10}} + 5{x^8}\frac{r}{x} + 10{x^6}{\left( {\frac{r}{x}} \right)^2} + 10{x^4}{\left( {\frac{r}{x}} \right)^3} + 5\left( {{x^2}} \right){\left( {\frac{r}{x}} \right)^4} + {\left( {\frac{r}{x}} \right)^5}\\ = {x^{10}} + 5{x^7}.r + 10{x^4}.{r^2} + 10x.{r^3} + 5.\frac{{{r^2}}}{{{x^2}}} + {\left( {\frac{r}{x}} \right)^5}\end{array}\)

Hệ số của x bằng 640 nên \(10{r^3} = 640 \Leftrightarrow {r^3} = 64 \Leftrightarrow r = 4\)

 

GIẢI SBT Toán 10 Kết nối tri thức Bài tập cuối chương 8

=========

THUỘC: Giải sách bài tập toán 10 – Kết nối