Giải SBT Bài 2: Các phép tính với số hữu tỉ – (C1 Toán 7 Chân trời)

Giải SBT Bài 2: Các phép tính với số hữu tỉ – (C1 Toán 7 Chân trời)

---

Giải bài 1 trang 10 SBT Toán 7 Chân trời sáng tạo tập 1

Tính:

a) \(\dfrac{3}{{10}} + \left( {\dfrac{{ – 5}}{{12}}} \right)\)

b) \(\dfrac{{ – 3}}{8} – \left( { – \dfrac{7}{{24}}} \right)\)

c) \(\left( {\dfrac{{ – 5}}{{14}}} \right) + 0,25\)

d) \(\left( { – \dfrac{7}{8}} \right) – 1,25\)

e) \(\left( {\dfrac{{ – 5}}{{14}}} \right).\dfrac{{21}}{{25}}\)

f) \(\dfrac{8}{{27}}:\left( { – \dfrac{{16}}{{45}}} \right)\)

g) \(\left( {1\dfrac{5}{6}} \right):\left( {4\dfrac{1}{8}} \right)\)

h) \(0,38.\left( { – \dfrac{7}{{19}}} \right)\)

i) \(\left( {\dfrac{{ – 4}}{5}} \right).\left( {\dfrac{{15}}{{ – 8}}} \right).1\dfrac{1}{9}\)

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Ta có thể viết các số hữu tỉ dưới dạng phân số rồi sau đó áp dụng qui tắc cộng, trừ phân số.

Lời giải chi tiết

\(\begin{array}{l}a)\dfrac{3}{{10}} + \left( {\dfrac{{ – 5}}{{12}}} \right) = \dfrac{{18}}{{60}} + \left( {\dfrac{{ – 25}}{{60}}} \right) = \dfrac{{ – 7}}{{60}}\\b)\dfrac{{ – 3}}{8} – \left( { – \dfrac{7}{{24}}} \right) = \dfrac{{ – 3}}{8} + \dfrac{7}{{24}} = \dfrac{{ – 9}}{{24}} + \dfrac{7}{{24}} = \dfrac{{ – 2}}{{24}} = \dfrac{{ – 1}}{{12}}\\c)\left( {\dfrac{{ – 5}}{{14}}} \right) + 0,25 = \left( {\dfrac{{ – 5}}{{14}}} \right) + \dfrac{1}{4} = \left( {\dfrac{{ – 10}}{{28}}} \right) + \dfrac{7}{{28}} = \dfrac{{ – 3}}{{28}}\\d)\left( { – \dfrac{7}{8}} \right) – 1,25 =  – \left( {\dfrac{7}{8} + \dfrac{5}{4}} \right) =  – \left( {\dfrac{7}{8} + \dfrac{{10}}{8}} \right) = \dfrac{{ – 17}}{8}\\e)\left( {\dfrac{{ – 5}}{{14}}} \right).\dfrac{{21}}{{25}} =  – \dfrac{{5.21}}{{14.25}} =  – \dfrac{{105}}{{350}} =  – \dfrac{{105:35}}{{350:35}} =  – \dfrac{3}{{10}}\\f)\dfrac{8}{{27}}:\left( { – \dfrac{{16}}{{45}}} \right) = \dfrac{8}{{27}}.\left( { – \dfrac{{45}}{{16}}} \right) =  – \dfrac{{8.45}}{{27.16}} =  – \dfrac{{8.9.5}}{{9.3.8.2}} =  – \dfrac{5}{6}\\g)\left( {1\dfrac{5}{6}} \right):\left( {4\dfrac{1}{8}} \right) = \dfrac{{11}}{6}:\dfrac{{33}}{8} = \dfrac{{11}}{6}.\dfrac{8}{{33}} = \dfrac{{11.2.4}}{{2.3.11.3}} = \dfrac{4}{9}\\h)0,38.\left( { – \dfrac{7}{{19}}} \right) = \dfrac{{38}}{{100}}.\left( { – \dfrac{7}{{19}}} \right) =  – \dfrac{{2.19.7}}{{2.50.19}} = \dfrac{{ – 7}}{{50}}\\i)\left( {\dfrac{{ – 4}}{5}} \right).\left( {\dfrac{{15}}{{ – 8}}} \right).1\dfrac{1}{9} = \dfrac{4}{5}.\dfrac{{15}}{8}.\dfrac{{10}}{9} = \dfrac{{4.15.10}}{{5.8.9}} = \dfrac{{4.3.5.5.2}}{{5.4.2.3.3}} = \dfrac{5}{2}\end{array}\)

---

Giải bài 2 trang 10 SBT Toán 7 Chân trời sáng tạo tập 1

Tính

a) \( – 0,375 + \dfrac{1}{4} – \left( { – \dfrac{1}{5}} \right)\)

b) \(\dfrac{2}{3} + \left( {\dfrac{{ – 5}}{{12}}} \right) + \left( {\dfrac{{ – 7}}{{15}}} \right) + ( – 0,2)\)

c) \(0,275 + \left( {\dfrac{{ – 8}}{{17}}} \right) + \dfrac{{29}}{{40}} + \left( {\dfrac{{ – 9}}{{17}}} \right) – 1\dfrac{1}{3}\)

d) \(\left( { – 5} \right).\left( {\dfrac{{ – 34}}{{21}}} \right).\left( {\dfrac{{ – 7}}{{10}}} \right).\left( { – \dfrac{3}{{17}}} \right)\)

e) \(\left( {\dfrac{{13}}{{18}}:\dfrac{{26}}{9}} \right).\dfrac{4}{7}\)

f) \(\left[ {\left( { – \dfrac{5}{{33}}} \right):\dfrac{2}{{11}}} \right].0,15\)

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Ta đổi những số hữu tỉ về dạng phân số sau đó áp dụng các qui tắc nhân chia phân số

Lời giải chi tiết

\(\begin{array}{l}a) – 0,375 + \dfrac{1}{4} – \left( { – \dfrac{1}{5}} \right) = \dfrac{{ – 3}}{8} + \dfrac{1}{4} + \dfrac{1}{5}\\ = \dfrac{{ – 15}}{{40}} + \dfrac{{10}}{{40}} + \dfrac{8}{{40}} = \dfrac{3}{{40}}\\b)\dfrac{2}{3} + \left( {\dfrac{{ – 5}}{{12}}} \right) + \left( {\dfrac{{ – 7}}{{15}}} \right) + ( – 0,2) = \dfrac{2}{3} – \dfrac{5}{{12}} – {\dfrac{7}{{15}} – \dfrac{1}{5}}\\ = \left( {\dfrac{2}{3} – \dfrac{5}{{12}}} \right) – \left( {\dfrac{7}{{15}} + \dfrac{1}{5}} \right) = \left( {\dfrac{8}{{12}} – \dfrac{5}{{12}}} \right) – \left( {\dfrac{7}{{15}} + \dfrac{3}{{15}}} \right)\\ = \dfrac{3}{{12}} – \dfrac{{10}}{{15}}= \dfrac{1}{{4}} – \dfrac{{2}}{{3}} = \dfrac{3}{{12}} – \dfrac{8}{{12}} = \dfrac{{ – 5}}{{12}}\\c)0,275 + \left( {\dfrac{{ – 8}}{{17}}} \right) + \dfrac{{29}}{{40}} + \left( {\dfrac{{ – 9}}{{17}}} \right) – 1\dfrac{1}{3}\\ = \dfrac{{11}}{{40}} + \left( {\dfrac{{ – 8}}{{17}}} \right) + \dfrac{{29}}{{40}} + \left( {\dfrac{{ – 9}}{{17}}} \right) – \dfrac{4}{3}\\ = \left( {\dfrac{{11}}{{40}} + \dfrac{{29}}{{40}}} \right) + \left[ {\left( {\dfrac{{ – 8}}{{17}}} \right) + \left( {\dfrac{{ – 9}}{{17}}} \right)} \right] – \dfrac{4}{3}\\ =\dfrac{40}{40}+\dfrac{-17}{17}-\dfrac{4}{3}= 1 + ( – 1) – \dfrac{4}{3} =  – \dfrac{4}{3}\\d)\left( { – 5} \right).\left( {\dfrac{{ – 34}}{{21}}} \right).\left( {\dfrac{{ – 7}}{{10}}} \right).\left( { – \dfrac{3}{{17}}} \right)\\ = 5.\dfrac{{34}}{{21}}.\dfrac{7}{{10}}.\dfrac{3}{{17}} = \dfrac{{5.34.7.3}}{{21.10.17}} = \dfrac{{5.17.2.7.3}}{{7.3.5.2.17}} = 1\\e)\left( {\dfrac{{13}}{{18}}:\dfrac{{26}}{9}} \right).\dfrac{4}{7} = \dfrac{{13}}{{18}}.\dfrac{9}{{26}}.\dfrac{4}{7} = \dfrac{{13.9.4}}{{18.26.7}} = \dfrac{{13.9.2.2}}{{2.9.13.2.7}} = \dfrac{1}{7}\\f)\left[ {\left( { – \dfrac{5}{{33}}} \right):\dfrac{2}{{11}}} \right].0,15 = \dfrac{{ – 5}}{{33}}.\dfrac{{11}}{2}.\dfrac{3}{{20}} =  – \dfrac{{5.11.3}}{{3.11.2.4.5}} = \dfrac{{ – 1}}{8}\end{array}\)

---

Giải bài 3 trang 10 SBT Toán 7 Chân trời sáng tạo tập 1

Thay dấu ? bằng dấu >, <, = thích hợp.

a) \(\left( {\dfrac{{ – 4}}{9}} \right) + \left( {\dfrac{5}{{ – 9}}} \right)\) ?  -1

b) \(\left( {\dfrac{{ – 13}}{{33}}} \right) + \left( {\dfrac{{ – 14}}{{33}}} \right)\) ? \(\dfrac{{ – 10}}{{11}}\)

c) \(\dfrac{1}{5} + \left( {\dfrac{{ – 2}}{3}} \right)\) ? \(\dfrac{2}{5} + \left( {\dfrac{{ – 4}}{5}} \right)\)

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Ta tính và tối giản các vế sau đó so sánh 2 vế với nhau (Áp dụng các qui tắc cộng, trừ, nhân, chia các phân số)

Lời giải chi tiết

a) Xét \(\left( {\dfrac{{ – 4}}{9}} \right) + \left( {\dfrac{5}{{ – 9}}} \right) = \dfrac{{ – 4}}{9} + \dfrac{{ – 5}}{9} = \dfrac{{ – 9}}{9} =  – 1\)

\( \Rightarrow \left( {\dfrac{{ – 4}}{9}} \right) + \left( {\dfrac{5}{{ – 9}}} \right) =  – 1\)

b) Xét \(\left( {\dfrac{{ – 13}}{{33}}} \right) + \left( {\dfrac{{ – 14}}{{33}}} \right) = \dfrac{{ – 13}}{{33}} + \dfrac{{ – 14}}{{33}} = \dfrac{{ – 27}}{{33}} = \dfrac{{ – 9}}{{11}}\)

Vì \(\dfrac{{ – 9}}{{11}} > \dfrac{{ – 10}}{{11}}\)

\( \Rightarrow \left( {\dfrac{{ – 13}}{{33}}} \right) + \left( {\dfrac{{ – 14}}{{33}}} \right) > \dfrac{{ – 10}}{{11}}\)

c) Xét \(\dfrac{1}{5} + \left( {\dfrac{{ – 2}}{3}} \right) = \dfrac{3}{{15}} + \dfrac{{ – 10}}{{15}} = \dfrac{{ – 7}}{{15}}\) và \(\dfrac{2}{5} + \left( {\dfrac{{ – 4}}{5}} \right) = \dfrac{2}{5} – \dfrac{4}{5} = \dfrac{{ – 2}}{5} = \dfrac{{ – 6}}{{15}}\)

Vì \(\dfrac{{ – 7}}{{15}} < \dfrac{{ – 6}}{{15}}\)

\( \Rightarrow \dfrac{1}{5} + \left( {\dfrac{{ – 2}}{3}} \right) < \dfrac{2}{5} + \left( {\dfrac{{ – 4}}{5}} \right)\)

---

Giải bài 4 trang 10 SBT Toán 7 Chân trời sáng tạo tập 1

Tính

a) \(\dfrac{6}{7}.\left( { – \dfrac{1}{8}} \right) + \dfrac{6}{7}.\left( { – \dfrac{3}{4}} \right)\)

b) \(\left( {\dfrac{{ – 7}}{{17}}} \right).\dfrac{5}{{12}} + \left( {\dfrac{{ – 7}}{{17}}} \right).\dfrac{7}{{12}} + \left( {\dfrac{{ – 10}}{{17}}} \right)\)

c) \(\left[ {\dfrac{3}{5} + \left( {\dfrac{{ – 1}}{4}} \right)} \right]:\dfrac{3}{7} + \left[ {\left( {\dfrac{{ – 3}}{4}} \right) + \dfrac{2}{5}} \right]:\dfrac{3}{7}\)

d) \(\dfrac{7}{8}:\left( {\dfrac{2}{9} – \dfrac{1}{{18}}} \right) + \dfrac{7}{8}:\left( {\dfrac{1}{{36}} – \dfrac{5}{{12}}} \right)\)

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Ta áp dụng các quy tắc cộng, trừ, nhân, chia các phân số

Lời giải chi tiết

\(a)\dfrac{6}{7}.\left( { – \dfrac{1}{8}} \right) + \dfrac{6}{7}.\left( { – \dfrac{3}{4}} \right) = \dfrac{6}{7}.\left( { – \dfrac{1}{8} – \dfrac{3}{4}} \right)\\ = \dfrac{6}{7}.\left( { – \dfrac{1}{8} – \dfrac{6}{8}} \right) = \dfrac{6}{7}.\left( { – \dfrac{7}{8}} \right) =  – \dfrac{6}{8} =  – \dfrac{3}{4}\\b)\left( {\dfrac{{ – 7}}{{17}}} \right).\dfrac{5}{{12}} + \left( {\dfrac{{ – 7}}{{17}}} \right).\dfrac{7}{{12}} + \left( {\dfrac{{ – 10}}{{17}}} \right)\\ = \left( {\dfrac{{ – 7}}{{17}}} \right).\left( {\dfrac{5}{{12}} + \dfrac{7}{{12}}} \right) + \left( {\dfrac{{ – 10}}{{17}}} \right)\\ = \left( {\dfrac{{ – 7}}{{17}}} \right).1 + \left( {\dfrac{{ – 10}}{{17}}} \right)\\ =\dfrac{-7}{17}+\dfrac{-10}{17}= \dfrac{{ – 17}}{{17}} =  – 1\\c)\left[ {\dfrac{3}{5} + \left( {\dfrac{{ – 1}}{4}} \right)} \right]:\dfrac{3}{7} + \left[ {\left( {\dfrac{{ – 3}}{4}} \right) + \dfrac{2}{5}} \right]:\dfrac{3}{7}\\ = \left( {\dfrac{{12}}{{20}} – \dfrac{5}{{20}}} \right):\dfrac{3}{7} + \left( {\dfrac{{ – 15}}{{20}} + \dfrac{8}{{20}}} \right):\dfrac{3}{7}\\ = \dfrac{7}{{20}}:\dfrac{3}{7} + \dfrac{{ – 7}}{{20}}:\dfrac{3}{7}\\ = \left( {\dfrac{7}{{20}} + \dfrac{{ – 7}}{{20}}} \right):\dfrac{3}{7} = 0.\dfrac{7}{3} = 0\\d)\dfrac{7}{8}:\left( {\dfrac{2}{9} – \dfrac{1}{{18}}} \right) + \dfrac{7}{8}:\left( {\dfrac{1}{{36}} – \dfrac{5}{{12}}} \right)\\ = \dfrac{7}{8}:\left( {\dfrac{4}{{18}} – \dfrac{1}{{18}}} \right) + \dfrac{7}{8}:\left( {\dfrac{1}{{36}} – \dfrac{{15}}{{36}}} \right)\\ = \dfrac{7}{8}: {\dfrac{3}{18}} + \dfrac{7}{8}:{\dfrac{{ – 14}}{{36}}}\\= \dfrac{7}{8}: {\dfrac{1}{6}} + \dfrac{7}{8}:{\dfrac{{ – 7}}{{18}}}\\ = \dfrac{7}{8}.6 + \dfrac{7}{8}.\dfrac{{ – 18}}{7} = \dfrac{{42}}{8} + \dfrac{{ – 18}}{8} = \dfrac{{24}}{8} = 3\)

---

Giải bài 5 trang 11 SBT Toán 7 Chân trời sáng tạo tập 1

Tìm x, biết:

a) \(x.\dfrac{{21}}{{25}} = \dfrac{{ – 7}}{{10}}\)

b) \(\dfrac{{ – 3}}{{20}}x = \dfrac{5}{{12}} – \dfrac{2}{5}\)

c) \(\dfrac{2}{9}:x = \dfrac{1}{{18}}:0,375\)

d) \(\left( { – \dfrac{{11}}{{12}}} \right):2x = \dfrac{5}{2} + \dfrac{1}{4}\)

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Tìm thừa số = tích : thừa số đã biết

Tìm số chia = số bị chia : thương

Lời giải chi tiết

\(\begin{array}{l}a)x.\dfrac{{21}}{{25}} = \dfrac{{ – 7}}{{10}}\\ \Leftrightarrow x = \dfrac{{ – 7}}{{10}}:\dfrac{{21}}{{25}}\\ \Leftrightarrow x = \dfrac{{ – 7}}{{10}}.\dfrac{{25}}{{21}}\\ \Leftrightarrow x = \dfrac{{ – 5}}{6}\end{array}\)

Vậy \(x = \dfrac{{ – 5}}{6}\)

\(\begin{array}{l}b)\dfrac{{ – 3}}{{20}}x = \dfrac{5}{{12}} – \dfrac{2}{5}\\ \Leftrightarrow \dfrac{{ – 3}}{{20}}x = \dfrac{{25}}{{60}} – \dfrac{{24}}{{60}}\\ \Leftrightarrow \dfrac{{ – 3}}{{20}}x = \dfrac{1}{{60}}\\ \Leftrightarrow x = \dfrac{1}{{60}}:\dfrac{{ – 3}}{{20}}\\ \Leftrightarrow x = \dfrac{1}{{60}}.\dfrac{{ – 20}}{3}\\ \Leftrightarrow x = \dfrac{{ – 1}}{9}\end{array}\)

Vậy \(x = \dfrac{{ – 1}}{9}\)

\(\begin{array}{l}c)\dfrac{2}{9}:x = \dfrac{1}{{18}}:0,375\\ \Leftrightarrow \dfrac{2}{9}:x = \dfrac{1}{{18}}:\dfrac{3}{8}\\ \Leftrightarrow \dfrac{2}{9}:x = \dfrac{1}{{18}}.\dfrac{8}{3}\\ \Leftrightarrow \dfrac{2}{9}:x = \dfrac{4}{{27}}\\ \Leftrightarrow x = \dfrac{2}{9}:\dfrac{4}{{27}}\\\Leftrightarrow x = \dfrac{2}{9}.\dfrac{27}{{4}}\\ \Leftrightarrow x = \dfrac{3}{2}\end{array}\)

Vậy \(x = \dfrac{3}{2}\)

\(\begin{array}{l}d)\left( { – \dfrac{{11}}{{12}}} \right):2x = \dfrac{5}{2} + \dfrac{1}{4}\\ \Leftrightarrow \left( { – \dfrac{{11}}{{12}}} \right):2x = \dfrac{{10}}{4} + \dfrac{1}{4}\\ \Leftrightarrow \left( { – \dfrac{{11}}{{12}}} \right):2x = \dfrac{{11}}{4}\\ \Leftrightarrow \left( { – \dfrac{{11}}{{12}}} \right):\dfrac{{11}}{4} = 2x\\ \Leftrightarrow \dfrac{{ – 11}}{{12}}.\dfrac{4}{{11}} = 2x\\ \Leftrightarrow \dfrac{{ – 1}}{3} = 2x\end{array}\)

\(\begin{array}{l} \Leftrightarrow x = \dfrac{{ – 1}}{3}:2\\\Leftrightarrow x = \dfrac{{ – 1}}{3}.\dfrac{1}{2}\\ \Leftrightarrow x = \dfrac{{ – 1}}{6}\end{array}\)

Vậy \(x = \dfrac{{ – 1}}{6}\)

---

Giải bài 6 trang 11 SBT Toán 7 Chân trời sáng tạo tập 1

Bảng dưới đây thể hiện lượng mưa (tính bằng mm) của một thành phố trong ba tháng so với lượng mưa trung bình trong năm. Hãy cho biết tổng lượng mưa trong khoảng thời gian ba tháng đó nhiều hơn hay ít hơn lượng mưa trung bình hàng năm. Giải thích.

Hướng dẫn giải chi tiết Bài 6

Phương pháp giải

Ta tính tổng lượng mưa chênh lệch của ba tháng.

+) Nếu kết quả là số dương thì lượng mưa trong 3 tháng nhiều hơn trung bình năm.

+) Nếu kết quả là số âm thì lượng mưa trong 3 tháng ít hơn trung bình năm.

Lời giải chi tiết

Ta có :

\(\begin{array}{l}95,8 + ( – 33,7) + ( – 83\dfrac{3}{5})\\ = 95,8{\rm{ }}-{\rm{ }}33,7{\rm{ }}-{\rm{ }}83,6\\ = {\rm{ }}62,1{\rm{ }}-{\rm{ }}83,6{\rm{ }} = {\rm{ }}-21,5\end{array}\)

Vậy tổng lượng mưa ba tháng ít hơn lượng mưa trung bình hàng năm là 21,5 mm.

---

Giải bài 7 trang 11 SBT Toán 7 Chân trời sáng tạo tập 1

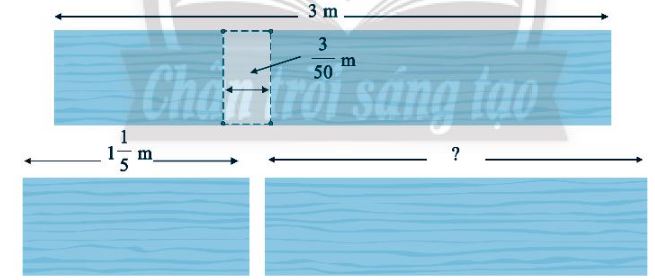
Sau khi ghép hai mảnh ván lại với nhau thì mảnh ván mới dài 3 m, phần ghép chung dài \(\dfrac{3}{{50}}\) m. Biết mảnh ván thứ nhất dài \(1\dfrac{1}{5}\)m. Tính chiều dài mảnh ván thứ hai.

Hướng dẫn giải chi tiết Bài 7

Phương pháp giải

Phần ghép chung là chèn lên của cả 2 mảnh nên độ dài 3m sẽ nhỏ hơn tổng độ dài thực tế 2 mảnh ván là 2 lần độ dài khoảng chèn lên nhau đó . Ta sẽ tính được độ dài của mảnh ván còn lại sau khi tính mảnh ván thứ nhất với số đo cho trước.

Lời giải chi tiết

Chiều dài hai mảnh ván sau khi ghép lại bằng tổng chiều dài hai mảnh ván ban đầu trừ đi phần ghép chung.

Khi đó, chiều dài mảnh ván thứ hai là:

\(3 – 1\dfrac{1}{5} + \dfrac{3}{{50}} = 3 – 1,2 + 0,06 = 1,86\) (m)

Vậy chiều dài mảnh ván thứ hai là 1,86 m.

---

Giải bài 8 trang 11 SBT Toán 7 Chân trời sáng tạo tập 1

Trong một bể nước, lượng nước chiếm đến \(\dfrac{3}{4}\)dung tích bể. Người ta mở một vòi nước chảy vào bể, mỗi giờ chảy được \(\dfrac{1}{8}\)bể. Hỏi nước chảy trong thời gian bao lâu thì đầy bể?

Hướng dẫn giải chi tiết Bài 8

Phương pháp giải

Ta tính lượng nước còn chảy để đầy bể là bao nhiêu . Sau đó lấy lượng nước đó chia cho thời gian nước chảy được mỗi giờ để tìm ra thời gian còn lại cần tìm.

Lời giải chi tiết

Số phần bể chưa chứa nước là:

\(1 – \dfrac{3}{4} = \dfrac{1}{4}\) (dung tích bể).

Thời gian chảy đầy bể là:

\(\dfrac{1}{4}:\dfrac{1}{8} = \dfrac{1}{4}.8 = 2\) (giờ).

Vậy nước chảy trong 2 giờ thì đầy bể.

---

Giải bài 9 trang 12 SBT Toán 7 Chân trời sáng tạo tập 1

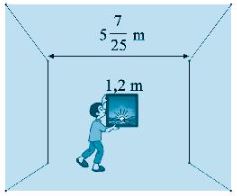
Huy muốn treo một bức tranh nằm giữa bức tường theo chiều ngang. Bức tường dài \(5\dfrac{7}{{25}}\) mét, bức tranh dài 1,2 m. Huy nên treo bức tranh cách mỗi mép tường là bao nhiêu mét?

Hướng dẫn giải chi tiết Bài 9

Phương pháp giải

Ta lấy chiều dài bức tường trừ đi chiều dài bức tranh, nhưng vì cách đều 2 bên tường nên ta cần lấy khoảng cách đó chia 2 thì sẽ ra khoảng các mà Huy phải treo để bức tranh nằm giữa.

Lời giải chi tiết

Chiều dài bức tường không bị che bởi bức tranh là:

\(5\dfrac{7}{{25}} – 1,2 = 5,28 – 1,2 = 4,08\) (m).

Chiều dài mỗi phần bức tường ở hai cạnh bức tranh là:

4,08 : 2 = 2,04 (m).

Vậy Huy phải treo bức tranh sao cho cạnh của bức tranh cách mép tường 2,04 m.

---

Giải bài 10 trang 12 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Bạn Mai nuôi một con mèo. Mai cho mèo ăn mỗi ngày 3 lần, mỗi lần 300 g thức ăn. Với lượng thức ăn có sẵn trong nhà là \(10\dfrac{4}{5}\) kg. Hỏi sau bao nhiêu ngày con mèo của bạn Mai ăn hết lượng thức ăn đó?

Hướng dẫn giải chi tiết Bài 10

Phương pháp giải

Ta sẽ tính (đổi) số thức ăn có sẵn ra số thập phân sau đó lấy số đó chia cho 300g (0,3kg) sẽ được số bữa ăn và từ đó tính số ngày mèo ăn hết lượng thức ăn đó.

Lời giải chi tiết

Đổi 300 g = 0,3 kg.

Khối lượng thức ăn Mai cho mèo ăn trong mỗi ngày là:

3 . 0,3 = 0,9 (kg).

Số ngày mèo của bạn Mai ăn hết lượng thức ăn đó là:

\(10\dfrac{4}{5}:0,9 = 10,8:0,9 = 12\) (ngày).

Vậy số ngày mèo của bạn Mai ăn hết lượng thức ăn đó là 12 ngày.

---

Giải bài 11 trang 12 SBT Toán 7 Chân trời sáng tạo tập 1

Một cửa hàng thời trang nhập về 100 cái áo với giá vốn mỗi cái là 200 000 đồng. Cửa hàng đã bán 60 cái áo, mỗi cái lời 25

Hướng dẫn giải chi tiết Bài 11

Phương pháp giải

Ta sẽ tính số tiền lãi 60 chiếc áo bán được và tính số tiền bán được 40 chiếc áo lỗ 5

Lời giải chi tiết

Cửa hàng đã bán 60 cái áo, mỗi cái lời 25

Khi đó, số tiền bán 60 cái áo này là:

60 . 200 000 . 125

Cửa hàng đã bán 40 cái áo còn lại cửa hàng bán lỗ 5

Khi đó, số tiền bán 40 cái áo này là:

40 . 200 000 . 95

Số tiền bán hết 100 cái áo là:

15 000 000 + 7 600 000 = 22 600 000 (đồng).

Số tiền mua 100 cái áo là:

100 . 200 000 = 20 000 000 (đồng).

Số tiền lời sau khi bán hết số áo đó là:

22 600 000 − 20 000 000 = 2 600 000 (đồng).

Vậy sau khi bán hết 100 cái áo cửa hàng đã lời 2 600 000 đồng.

---

Giải bài 12 trang 12 SBT Toán 7 Chân trời sáng tạo tập 1

Đỉnh núi Ngọc Linh (Kon Tum) có độ cao khoảng bằng 0,78 lần đỉnh núi Phan Xi Păng. Đỉnh núi Bà Đen (Tây Ninh) cao khoảng bằng \(\dfrac{2}{5}\) lần đỉnh núi Ngọc Linh.

a) Đỉnh núi Bà Đen cao bằng bao nhiêu phần đỉnh núi Phan Xi Păng?

b) Đỉnh núi Bà Đen cao khoảng 980 m. Tính độ cao đỉnh núi Ngọc Linh và độ cao đỉnh núi Phan Xi Păng.

Hướng dẫn giải chi tiết Bài 12

Phương pháp giải

a) Ta đổi 0,78 ra phân số sau đó lấy số đó nhân với \(\dfrac{2}{5}\) sẽ ra được tỉ số giữa núi Bà Đen và đỉnh núi Phan Xi Păng

b)Tìm a biết \(\dfrac{m}{n}\) là b, ta tính: \(a = b:\dfrac{m}{n}\)

Lời giải chi tiết

a) Đỉnh núi Bà Đen cao bằng số phần phần đỉnh núi Phan Xi Păng là:

\(0,78.\dfrac{2}{5} = \dfrac{{39}}{{125}}\) (đỉnh núi Phan Xi Păng).

Vậy đỉnh núi Bà Đen cao bằng\(\dfrac{{39}}{{125}}\) đỉnh núi Phan Xi Păng.

b) Đỉnh núi Ngọc Linh có độ cao là:

\(980:\dfrac{2}{5} = 2450\) (m).

Đỉnh núi Phan Xi Păng có độ cao là:

2450 : 0,78 ≈ 3141 (m).

Vậy đỉnh núi Ngọc Linh cao 2 450 m và đỉnh núi Phan Xi Păng cao khoảng 3 141 m.