Giải bài tập Bài 4: Bất phương trình bậc hai một ẩn (C3 – Toán 10 Cánh diều)
Giải bài tập Bài 1 trang 54 SGK Toán 10 Cánh diều tập 1
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc hai một ẩn? Vì sao?
a) \( – 2x + 2 < 0\)
b) \(\frac{1}{2}{y^2} – \sqrt 2 \left( {y + 1} \right) \le 0\)
c) \({y^2} + {x^2} – 2x \ge 0\)
Phương pháp giải
– Xác định bậc của bất phương trình.
– Xác định số ẩn của bất phương trình.
Hướng dẫn giải
a) \( – 2x + 2 < 0\) không là bất phương trình bậc hai một ẩn vì bậc của bất phương trình này là bậc 1.
b) \(\frac{1}{2}{y^2} – \sqrt 2 \left( {y + 1} \right) \le 0\) là bất phương trình bậc hai một ẩn vì bậc của bất phương trình này là bậc 2 và có đúng 1 ẩn là y.
c) \({y^2} + {x^2} – 2x \ge 0\) không là bất phương trình bậc hai một ẩn vì có 2 ẩn là x và y.
Giải bài tập Bài 2 trang 54 SGK Toán 10 Cánh diều tập 1
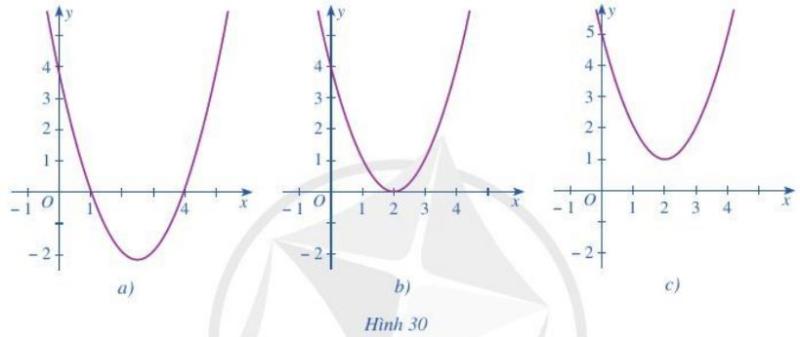
Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;\)\(f\left( x \right) \ge 0;f\left( x \right) \le 0\).

Phương pháp giải
– Quan sát đồ thị.
– Phần phía trên trục hoành biểu diễn tập nghiệm của bất phương trình \(f\left( x \right) > 0\)(không tính giao điểm với đồ thị)
– Phần phía dưới trục hoành biểu diễn tập nghiệm của bất phương trình \(f\left( x \right) < 0\)(không tính giao điểm với đồ thị)
Hướng dẫn giải
Hình 30a:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \left( { – \infty ;1} \right) \cup \left( {4; + \infty } \right)\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \left( {1;4} \right)\)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \left( { – \infty ;1} \right] \cup \left[ {4; + \infty } \right)\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left[ {1;4} \right]\)
Hình 30b:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left\{ 2 \right\}\)
Hình 30c:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \emptyset \)
Giải bài tập Bài 3 trang 54 SGK Toán 10 Cánh diều tập 1
Giải các bất phương trình bậc hai sau:
a) \(2{x^2} – 5x + 3 > 0\)
b) \( – {x^2} – 2x + 8 \le 0\)
c) \(4{x^2} – 12x + 9 < 0\)
d) \( – 3{x^2} + 7x – 4 \ge 0\)
Phương pháp giải
Giải bài tập Bất phương trình dạng \(f\left( x \right) > 0\).
Bước 1: Xác định dấu của hệ số a và tìm nghiệm của \(f\left( x \right)\)(nếu có)
Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho \(f\left( x \right)\) mang dấu “+”
Bước 3: Các bất phương trình bậc hai có dạng \(f\left( x \right) < 0,f\left( x \right) \ge 0,f\left( x \right) \le 0\) được Giải bài tập Bằng cách tương tự.
Hướng dẫn giải
a) Ta có \(a = 2 > 0\) và \(\Delta = {\left( { – 5} \right)^2} – 4.2.3 = 1 > 0\)
=> \(2{x^2} – 5x + 3 = 0\) có 2 nghiệm phân biệt \({x_1} = 1,{x_2} = \frac{3}{2}\).
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} – 5x + 3\) mang dấu “+” là \(\left( { – \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \(2{x^2} – 5x + 3 > 0\) là \(\left( { – \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)
b) Ta có \(a = – 1 < 0\) và \(\Delta ‘ = {\left( { – 1} \right)^2} – \left( { – 1} \right).8 = 9 > 0\)
=> \( – {x^2} – 2x + 8 = 0\)có 2 nghiệm phân biệt \({x_1} = – 4,{x_2} = 2\).
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( – {x^2} – 2x + 8\) mang dấu “-” là \(\left( { – \infty ; – 4} \right] \cup \left[ {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \( – {x^2} – 2x + 8 \le 0\) là \(\left( { – \infty ; – 4} \right] \cup \left[ {2; + \infty } \right)\)
c)
Ta có \(a = 4 > 0\) và \(\Delta ‘ = {\left( { – 6} \right)^2} – 4.9 = 0\)
=> \(4{x^2} – 12x + 9 = 0\) có nghiệm duy nhất \(x = \frac{3}{2}\).
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(4{x^2} – 12x + 9\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(4{x^2} – 12x + 9 < 0\) là \(\emptyset \)
d) \( – 3{x^2} + 7x – 4 \ge 0\)
Ta có \(a = – 3 < 0\) và \(\Delta = {7^2} – 4.\left( { – 3} \right).\left( { – 4} \right) = 1 > 0\)
=> \( – 3{x^2} + 7x – 4 = 0\) có 2 nghiệm phân biệt \({x_1} = 1;{x_2} = \frac{4}{3}\).
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( – 3{x^2} + 7x – 4\) mang dấu “+” là \(\left[ {1;\frac{4}{3}} \right]\)
Vậy tập nghiệm của bất phương trình \( – 3{x^2} + 7x – 4 \ge 0\) là \(\left[ {1;\frac{4}{3}} \right]\)
Giải bài tập Bài 4 trang 54 SGK Toán 10 Cánh diều tập 1
Tìm m để phương trình \(2{x^2} + \left( {m + 1} \right)x + m – 8 = 0\) có nghiệm.
Phương pháp giải
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có nghiệm khi và chỉ khi \(\Delta = {b^2} – 4ac \ge 0\).
Hướng dẫn giải
Ta có \(a = 2 > 0\),
\(\Delta = {\left( {m + 1} \right)^2} – 4.2.\left( {m – 8} \right)\)\( = {m^2} + 2m + 1 – 8m + 64\)\( = {m^2} – 6m + 65\)
Phương trình \(2{x^2} + \left( {m + 1} \right)x + m – 8 = 0\) có nghiệm khi và chỉ khi \(\Delta \ge 0\)
Vậy phương trình \(2{x^2} + \left( {m + 1} \right)x + m – 8 = 0\) có nghiệm với mọi số thực m.
Giải bài tập Bài 5 trang 54 SGK Toán 10 Cánh diều tập 1
Xét hệ toạ độ Oth trên mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,2) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8,5 m sau 1 giây và đạt độ cao 6 m sau 2 giây.
a) Hãy tìm hàm số bậc hai biểu thị quỹ đạo chuyển động của quả bóng.
b) Trong khoảng thời gian nào thì quả bóng vẫn chưa chạm đất?
Phương pháp giải
a) Đặt phương trình parabol là \(\left( P \right):h = a{t^2} + bt + c\)
Thay tọa độ điểm A, điểm (1;8,5) và điểm (2;6) vào tìm a, b và c.
b) Tìm t để h>0
Hướng dẫn giải
a) Đặt phương trình parabol là \(\left( P \right):h = a{t^2} + bt + c\)
Ta có quả bóng được đá lên từ điểm A(0; 0,2) nên \(0,2 = c\)
Ta có quả bóng đạt độ cao 8,5 m sau 1 giây có nghĩa là tại t=1 thì h=8,5. Khi đó
\(8,5 = a + b\)(1)
Ta có quả bóng đạt độ cao 6 m sau 2 giây có nghĩa là tại t=2 thì h=6.
=> \(6 = a{.2^2} + b.2\)\( \Leftrightarrow 4a + 2b = 6\left( 2 \right)\)
Từ (1) và (2) ta được hệ \(\left\{ \begin{array}{l}a + b = 8,5\\4a + 2b = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – 5,5\\b = 14\end{array} \right.\)
Vậy \(\left( P \right):h = – 5,5{t^2} + 14t\)
b) Để quả bóng không chạm đất thì \(h > 0\)
\(\begin{array}{l} \Leftrightarrow – 5,5{t^2} + 14t > 0\\ \Leftrightarrow t\left( { – 5,5t + 14} \right) > 0\\ \Leftrightarrow 0 < t < \frac{{28}}{{11}}\end{array}\)
Vậy trong khoảng thời gian từ lúc đá đến thời gian \(t = \frac{{28}}{{11}}\) thì quả bóng chưa chạm đất.
