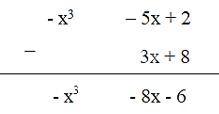
Giải bài tập Bài 26 Phép cộng và phép trừ đa thức một biến (Chương 7 Toán 7 Kết nối)
============
Giải bài 7.12 trang 33 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Tìm tổng của hai đa thức sau bằng cách nhóm các hạng tử cùng bậc: x2 – 3x + 2 và 4x3 – x2 + x – 1
Hướng dẫn giải chi tiết Giải bài 7.12
Phương pháp giải
Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Lời giải chi tiết
Ta có: (x2 – 3x + 2) + (4x3 – x2 + x – 1)
= x2 – 3x + 2 + 4x3 – x2 + x – 1
= 4x3 + (x2 – x2 ) + (-3x + x) + (2 – 1)
= 4x3 – 2x + 1
–>
— *****
Giải bài 7.13 trang 33 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Tìm hiệu sau theo cách đặt tính trừ: \(( – {\rm{ }}{x^3}–5x + 2)–\left( {3x + 8} \right)\)
Hướng dẫn giải chi tiết Giải bài 7.13
Phương pháp giải
Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.
Lời giải chi tiết
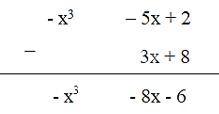
–>
— *****
Giải bài 7.14 trang 33 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Cho hai đa thức: \(A = 6{x^4} – 4{x^3} + x – \dfrac{1}{3};B = – 3{x^4} – 2{x^3} – 5{x^2} + x + \dfrac{2}{3}\). Tính A + B và A – B
Hướng dẫn giải chi tiết Giải bài 7.14
Phương pháp giải
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng (trừ) sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng (trừ ) theo từng cột.
Lời giải chi tiết
Cách 1:
\(\begin{array}{l}A + B = (6{x^4} – 4{x^3} + x – \dfrac{1}{3}) + ( – 3{x^4} – 2{x^3} – 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} – 4{x^3} + x – \dfrac{1}{3} – 3{x^4} – 2{x^3} – 5{x^2} + x + \dfrac{2}{3}\\ = (6{x^4} – 3{x^4}) + ( – 4{x^3} – 2{x^3}) – 5{x^2} + (x + x) + ( – \dfrac{1}{3} + \dfrac{2}{3})\\ = 3{x^4} – 6{x^3} – 5{x^2} + 2x + \dfrac{1}{3}\\A – B = (6{x^4} – 4{x^3} + x – \dfrac{1}{3}) – ( – 3{x^4} – 2{x^3} – 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} – 4{x^3} + x – \dfrac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} – x – \dfrac{2}{3}\\ = (6{x^4} + 3{x^4}) + ( – 4{x^3} + 2{x^3}) + 5{x^2} + (x – x) + ( – \dfrac{1}{3} – \dfrac{2}{3})\\ = 9{x^4} – 2{x^3} + 5{x^2} – 1\end{array}\)\(\begin{array}{l}A + B = (6{x^4} – 4{x^3} + x – \dfrac{1}{3}) + ( – 3{x^4} – 2{x^3} – 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} – 4{x^3} + x – \dfrac{1}{3} – 3{x^4} – 2{x^3} – 5{x^2} + x + \dfrac{2}{3}\\ = (6{x^4} – 3{x^4}) + ( – 4{x^3} – 2{x^3}) – 5{x^2} + (x + x) + ( – \dfrac{1}{3} + \dfrac{2}{3})\\ = 3{x^4} – 6{x^3} – 5{x^2} + 2x + \dfrac{1}{3}\\A – B = (6{x^4} – 4{x^3} + x – \dfrac{1}{3}) – ( – 3{x^4} – 2{x^3} – 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} – 4{x^3} + x – \dfrac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} – x – \dfrac{2}{3}\\ = (6{x^4} + 3{x^4}) + ( – 4{x^3} + 2{x^3}) + 5{x^2} + (x – x) + ( – \dfrac{1}{3} – \dfrac{2}{3})\\ = 9{x^4} – 2{x^3} + 5{x^2} – 1\end{array}\)
Cách 2:
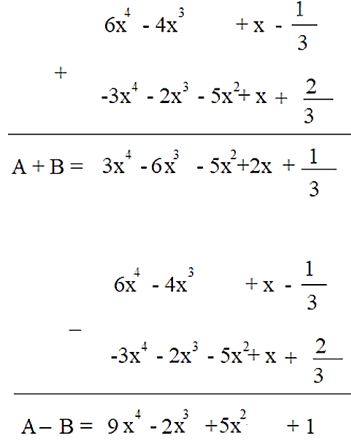
–>
— *****
Giải bài 7.15 trang 33 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Cho các đa thức: \(A = 3{x^4} – 2{x^3} – x + 1;B = – 2{x^3} + 4{x^2} + 5x;C = – 3{x^4} + 2{x^2} + 5\). Tính A + B + C; A – B + C và A – B – C
Hướng dẫn giải chi tiết Giải bài 7.15
Phương pháp giải
Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Lời giải chi tiết
\(\begin{array}{l}A + B + C = (3{x^4} – 2{x^3} – x + 1) + ( – 2{x^3} + 4{x^2} + 5x) + ( – 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} – 2{x^3} – x + 1 – 2{x^3} + 4{x^2} + 5x – 3{x^4} + 2{x^2} + 5\\ = (3{x^4} – 3{x^4}) + ( – 2{x^3} – 2{x^3}) + (4{x^2} + 2{x^2}) + ( – x + 5x) + (1 + 5)\\ = 0 + ( – 4{x^3}) + 6{x^2} + 4x + 6\\ = – 4{x^3} + 6{x^2} + 4x + 6\\A – B + C = (3{x^4} – 2{x^3} – x + 1) – ( – 2{x^3} + 4{x^2} + 5x) + ( – 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} – 2{x^3} – x + 1 + 2{x^3} – 4{x^2} – 5x – 3{x^4} + 2{x^2} + 5\\ = (3{x^4} – 3{x^4}) + ( – 2{x^3} + 2{x^3}) + ( – 4{x^2} + 2{x^2}) + ( – x – 5x) + (1 + 5)\\ = 0 + 0 + ( – 2{x^2}) – 6x + 6\\ = – 2{x^2} – 6x + 6\\A – B – C = (3{x^4} – 2{x^3} – x + 1) – ( – 2{x^3} + 4{x^2} + 5x) – ( – 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} – 2{x^3} – x + 1 + 2{x^3} – 4{x^2} – 5x + 3{x^4} – 2{x^2} – 5\\ = (3{x^4} + 3{x^4}) + ( – 2{x^3} + 2{x^3}) + ( – 4{x^2} – 2{x^2}) + ( – x – 5x) + (1 – 5)\\ = 6{x^4} + 0 + ( – 6{x^2}) – 6x + ( – 4)\\ = 6{x^4} – 6{x^2} – 6x – 4\end{array}\)
–>
— *****
Giải bài 7.16 trang 33 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
Bạn Nam được phân công mua một số sách làm quà tặng trong buổi tổng kết cuối năm học của lớp. Nam dự định mau ba loại sách với giá bán như bảng sau. Giả sử Nam cần mua x cuốn sách khoa học, x+8 cuốn sách tham khảo và x + 5 cuốn truyện tranh.
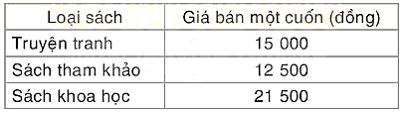
a) Viết các đa thức biểu thị số tiền Nam phải trả cho từng loại sách.
b) Tìm đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó.
Hướng dẫn giải chi tiết Giải bài 7.16
Phương pháp giải
Viết đa thức biểu thị số tiền
Tiền mua 1 loại sách = số cuốn . giá tiền một cuốn
Lời giải chi tiết
a) Đa thức biểu thị số tiền Nam phải trả cho truyện tranh là: A = (x +5). 15 000 = 15 000x + 75 000 ( đồng)
Đa thức biểu thị số tiền Nam phải trả cho sách tham khảo là: B = (x + 8) . 12 500 = 12 500x + 100 000 ( đồng)
Đa thức biểu thị số tiền Nam phải trả cho sách khoa học là: C = x . 21 500 (đồng)
b) Đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó là:
P = A + B + C = = 15 000x + 75 000 + 12 500x + 100 000 + x . 21 500
= (15 000 + 12 500 + 21 500)x + (75 000 + 100 000)
= 49 000x + 175 000 ( đồng)
–>
— *****
Giải bài 7.17 trang 33 SGK Toán 7 Kết nối tri thức tập 2 – KNTT
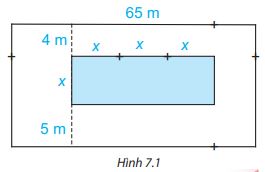
Trên một mảnh đất hình chữ nhật có chiều dài 65 m, người ta định làm một bể bơi có chiều rộng là x nét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) đươc cho trong Hình 7.1. Tìm đa thức ( biến x):
a) Biểu thị diện tích bể bơi
b) Biểu thị diện tích mảnh đất
c) Biểu thị diện tích phần đất xung quanh bể bơi.
Hướng dẫn giải chi tiết Giải bài 7.17
Phương pháp giải
+ Biểu thị chiều dài và chiều rộng của các hình chữ nhật
Diện tích hình chữ nhật = chiều dài . chiều rộng
Lời giải chi tiết
a) Bể bơi có chiều dài là 3x, chiều rộng là x nên đa thức biểu thị diện tích bể bơi là:
B = 3x. x = 3.x2
b) Mảnh đất có chiều dài là 65, chiều rộng là 5 + x + 4 = x + 9 nên đa thức biểu thị diện tích mảnh đất là:
D = 65. (x+9) = 65x + 585
c) Diện tích xung quanh bể bơi = diện tích mảnh đất – diện tích bể bơi nên đa thức biểu thị diện tích phần đất xung quanh bể bơi là:
Q = D – B = 65x + 585 – 3.x2 = -3.x2 +65x + 585
–>
— *****
