Giải bài tập Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng sogn song (C3 Toán 7 Kết nối)

Giải bài tập Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng sogn song (C3 Toán 7 Kết nối)
——————

Giải bài 3.17 trang 53 SGK Toán 7 KNTT tập 1

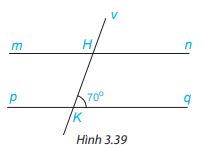
Cho Hình 3.39, biết rằng mn//pq. Tính số đo các góc Mhk, VHn.

Phương pháp giải

Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì:

Hai góc so le trong bằng nhau

Hai góc đồng vị bằng nhau

Lời giải chi tiết

Vì mn//pq nên

+) \(\widehat {mHK} = \widehat {HKq}\) ( 2 góc so le trong), mà \(\widehat {HKq} = 70^\circ  \Rightarrow \widehat {mHK} = 70^\circ \)

+) \(\widehat {vHn} = \widehat {HKq}\) ( 2 góc đồng vị). mà \(\widehat {HKq} = 70^\circ  \Rightarrow \widehat {vHn} = 70^\circ \)

Giải bài 3.18 trang 53 SGK Toán 7 KNTT tập 1

Cho Hình 3.40

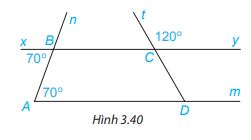
a) Giải thích tại sao Am//By

b) Tính \(\widehat {CDm}\)

Phương pháp giải

a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

b) Sử dụng tính chất của 2 đường thẳng song song

Lời giải chi tiết

a) Vì \(\widehat {xBA} = \widehat {BAD}( = 70^\circ )\), mà 2 góc này ở vị trí so le trong nên Am // By ( Dấu hiệu nhận biết 2 đường thẳng song song.)

b) Vì Am // By nên \(\widehat {CDm} = \widehat {tCy}\) ( 2 góc đồng vị), mà \(\widehat {tCy} = 120^\circ  \Rightarrow \widehat {CDm} = 120^\circ \).

Giải bài 3.19 trang 54 SGK Toán 7 KNTT tập 1

Cho Hình 3.41.

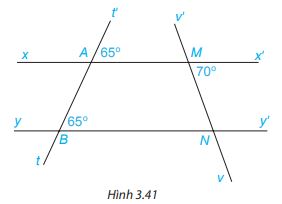
a) Giải thích tại sao xx’//yy’.

b) Tính số đo góc MNB.

Phương pháp giải

a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

b) Sử dụng tính chất của 2 đường thẳng song song

Lời giải chi tiết

a) Vì \(\widehat {t’AM} = \widehat {ABN}( = 65^\circ )\), mà 2 góc này ở vị trí đồng vị nên xx’//yy’ ( Dấu hiệu nhận biết 2 đường thẳng song song.)

b) Vì xx’//yy’ nên \(\widehat {x’MN} = \widehat {MNB}\)( 2 góc so le trong), mà \(\widehat {x’MN} = 70^\circ  \Rightarrow \widehat {MNB} = 70^\circ \)

Giải bài 3.20 trang 54 SGK Toán 7 KNTT tập 1

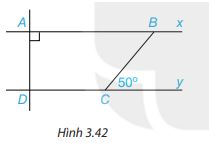
Cho Hình 3.42, biết rằng Ax//Dy, \(\widehat A = 90^\circ ,\widehat {BCy} = 50^\circ \). Tính số đo các góc ADC và ABC.

Phương pháp giải

Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì:

Hai góc so le trong bằng nhau

Hai góc đồng vị bằng nhau

Lời giải chi tiết

Vì Ax // Dy, mà AD \( \bot \) Ax nên AD \( \bot \) Dy. Do đó,

Vì Ax // Dy nên \(\widehat {ABC} = \widehat {BCy}\) ( 2 góc so le trong), mà \(\widehat {BCy} = 50^\circ  \Rightarrow \widehat {ABC} = 50^\circ \)

Giải bài 3.21 trang 54 SGK Toán 7 KNTT tập 1 – KNTT

Cho Hình 3.43. Giải thích tại sao:

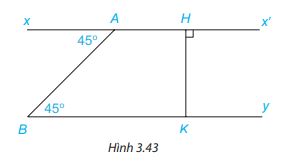
a) Ax’ // By    

b) By \( \bot \) HK

Phương pháp giải

a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

b) Sử dụng tính chất đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì vuông góc với đường thẳng kia

Lời giải chi tiết

a) Vì \(\widehat {xAB} = \widehat {ABy}( = 45^\circ )\), mà hai góc này ở vị trí so le trong nên Ax’ // By ( Dấu hiệu nhận biết 2 đường thẳng song song.)

b) Vì Ax’ // By, mà By \( \bot \) HK nên Ax’ \( \bot \) HK

Giải bài 3.22 trang 54 SGK Toán 7 KNTT tập 1

Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thằng b? Vì sao?

Phương pháp giải

Dựa vào tiên đề Euclid: Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.

Lời giải chi tiết

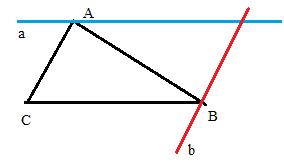
Theo Tiên đề Euclid:

+) Qua điểm A nằm ngoài đường thẳng BC, chỉ có một đường thẳng song song với đường thẳng BC. Đường thẳng đó là a

+) Qua điểm B nằm ngoài đường thẳng AC, chỉ có một đường thẳng song song với đường thẳng BC. Đường thẳng đó là b

Như vậy, có thể vẽ được 1 đường thẳng a, 1 đường thẳng b.

Giải bài 3.23 trang 54 SGK Toán 7 KNTT tập 1

Cho Hình 3.44. Giải thích tại sao:

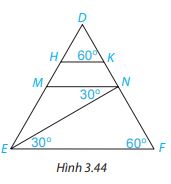
a) MN//EF

b) HK//EF

c) HK//MN

Phương pháp giải

Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

Sử dụng tính chất 2 đường thẳng cùng song song với 1 đường thẳng thứ ba thì chúng song song với nhau.

Lời giải chi tiết

a) Vì \(\widehat {MNE} = \widehat {NEF}( = 30^\circ )\), mà 2 góc này ở vị trí so le trong nên MN//EF ( Dấu hiệu nhận biết 2 đường thẳng song song.)

b) Vì \(\widehat {DKH} = \widehat {DFE}( = 60^\circ )\), mà 2 góc này ở vị trí đồng vị nên HK//EF ( Dấu hiệu nhận biết 2 đường thẳng song song.)

c) Vì MN//EF; HK//EF nên HK//MN