Giải Bài 3. Parabol – Chuyên đề Toán 10 CD

Giải CHI TIẾT Bài 3. Parabol – Chuyên đề Toán 10 CD
=================

Giải mục 1 trang 57 Chuyên đề học tập Toán 10 – Cánh diều>

Lựa chọn câu để xem lời giải nhanh hơn

• HĐ 1

HĐ 1

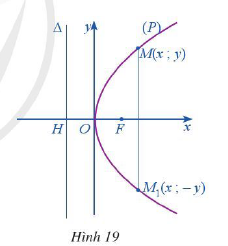
Trong mặt phẳng tọa độ \(Oxy\), ta xét parabol (P) với phương trình chính tắc \({y^2} = 2px\) trong đó \(p > 0\) (Hình 19)

 

a) Tìm tọa độ của tiêu điểm F của parabol (P)

b) Tìm tọa độ điểm H và viết phương trình đường chuẩn \(\Delta \) của parabol (P)

c) Cho điểm \(M\left( {x;y} \right)\) nằm trên parabol (P). Gọi \({M_1}\) là điểm đối xứng của M qua trục Ox. Điểm \({M_1}\) có nằm trên parabol (P) không? Tại sao?

Lời giải chi tiết:

a) Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)

b) Điểm H có tọa độ \(H\left( { – \frac{p}{2};0} \right)\). Đường chuẩn: \(\Delta : x =  – \frac{p}{2}\)

c) \({M_1}\) đối xứng với \(M(x;y)\) qua Ox nên \({M_1}(x; – y)\)

\({M_1}(x; – y) \in (P)\) vì \({( – y)^2} = 2px\)

Giải mục 1 trang 57 Chuyên đề học tập Toán 10 – Cánh diều

Giải mục 2 trang 58 Chuyên đề học tập Toán 10 – Cánh diều>

Lựa chọn câu để xem lời giải nhanh hơn

• HĐ 2
• Luyện tập

HĐ 2

Trong mặt phẳng tọa độ \(Oxy\), ta xét parabol (P) với phương trình chính tắc \({y^2} = 2px\) trong đó \(p > 0\) (Hình 20)

 

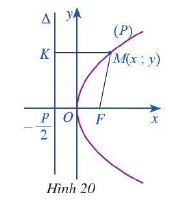
a) So sánh khoảng cách từ MF từ điểm M đến tiêu điểm F và khoảng cách MK từ điểm M đến đường thẳng \(\Delta \)

b) Tính độ dài đoạn thẳng MK. Từ đó tính độ dài đoạn thẳng MF

Phương pháp giải:

Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)

+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)

+ Đường chuẩn: \(\Delta : x =  – \frac{p}{2}\)

Lời giải chi tiết:

a) Khoảng cách MF từ điểm M đến tiêu điểm F bằng khoảng cách MK từ điểm M đến đường chuẩn \(\Delta \)

b) Ta có

\(MF = \sqrt {{{\left( {x – \frac{p}{2}} \right)}^2} + {y^2}}  = \sqrt {{x^2} – px + \frac{{{p^2}}}{4} + 2px}  = \sqrt {{x^2} + px + \frac{{{p^2}}}{4}}  = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}}  = x + \frac{p}{2}\)

Phương trình đường chuẩn \(\Delta : x =  – \frac{p}{2} \Rightarrow \Delta : x + 0y + \frac{p}{2} = 0\)

Khoảng cách MK từ điểm M đến đường thẳng \(\Delta \) là: \(MK = \frac{{\left| {x + 0y + \frac{p}{2}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \left| {x + \frac{p}{2}} \right| = x + \frac{p}{2}\)

Vậy \(MF = MK = x + \frac{p}{2}\)

 

Luyện tập

a) Lập phương trình chính tắc của parabol (P), biết phương trình đường chuẩn là \(x =  – 2\)

b) Tìm tọa độ tiêu điểm của parabol (P)

c) Tìm tọa độ điểm M thuộc parabol (P), biết khoảng cách từ M đến tiêu điểm bằng 6

Phương pháp giải:

Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)

+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)

+ Đường chuẩn: \(\Delta : x =  – \frac{p}{2}\)

Lời giải chi tiết:

a) Ta có phương trình đường chuẩn \(x =  – 2 \Rightarrow \frac{p}{2} = 2 \Rightarrow p = 4\)

Vậy phương trình chính tắc của parabol (P) là \({y^2} = 8x\)

b) Tiêu điểm của parabol (P) là \(F\left( {2;0} \right)\)

c) Khoảng cách từ M đến tiêu điểm \(F\left( {2;0} \right)\) bằng 6 nên \(x + \frac{p}{2} = 6 \Rightarrow x + 2 = 6 \Rightarrow x = 4 \Rightarrow {y^2} = 8.4 \Rightarrow y =  \pm 4\sqrt 2 \)

Vậy \(M\left( {4; \pm 4\sqrt 2 } \right)\)

Giải mục 2 trang 58 Chuyên đề học tập Toán 10 – Cánh diều
=============

Giải mục 3 trang 58 Chuyên đề học tập Toán 10 – Cánh diều>

Lựa chọn câu để xem lời giải nhanh hơn

• HĐ 3
• Luyện tập

HĐ 3

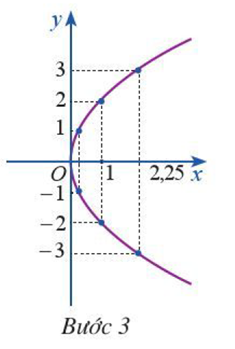
Vẽ parabol (P): \({y^2} = 4x\)

Lời giải chi tiết:

Để vẽ parabol (P): \({y^2} = 4x\) ta có thể làm như sau:

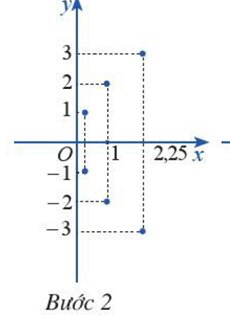
Bước 1: Lập bảng giá trị

x	0	0,25	0,25	1	1	2,25	2,25
y	0	-1	1	2	-2	-3	3

Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau

Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị

 

Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2

 

Luyện tập

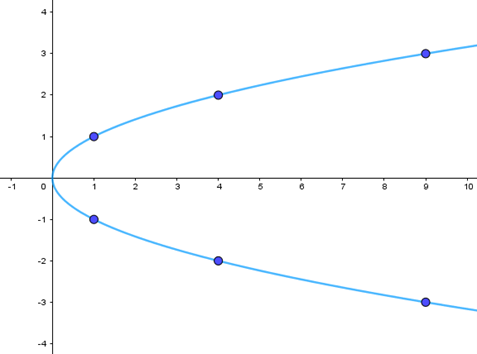
Vẽ parabol \({y^2} = 2px\) biết tiêu điểm của parabol là \(F\left( {\frac{1}{4};0} \right)\)

Phương pháp giải:

Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)

+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)

Lời giải chi tiết:

Ta có tiêu điểm của parabol là \(F\left( {\frac{1}{4};0} \right)\) nên \(\frac{p}{2} = \frac{1}{4} \Rightarrow p = \frac{1}{2} \Rightarrow {y^2} = x\)

Để vẽ parabol (P): \({y^2} = x\) ta có thể làm như sau:

Bước 1: Lập bảng giá trị

x	0	1	1	4	4	9	9
y	0	-1	1	2	-2	-3	3

Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau

Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị

Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2

 

Giải mục 3 trang 58 Chuyên đề học tập Toán 10 – Cánh diều
===============

Giải bài 1 trang 58 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Viết phương trình chính tắc của parabol (P) trong mỗi trường hợp sau:

a) Tiêu điểm là \({F_2}\left( {5;0} \right)\)

b) Phương trình đường chuẩn là \(x =  – 4\)

c) Parabol đi qua điểm \(A\left( {4;9} \right)\)

Phương pháp giải

Phương pháp

Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)

+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)

+ Đường chuẩn: \(\Delta : x =  – \frac{p}{2}\)

Lời giải chi tiết

a) Tiêu điểm là \({F_2}\left( {5;0} \right)\)

+ Parabol có tiêu điểm là \({F_2}\left( {5;0} \right) \Rightarrow \frac{p}{2} = 5 \Rightarrow p = 10\)

Khi đó phương trình chính tắc của parabol là: \({y^2} = 20x\)

b) Phương trình đường chuẩn là \(x =  – 4\)

+ Parabol có phương trình đường chuẩn là \(x =  – 4 \Rightarrow \frac{p}{2} = 4 \Rightarrow p = 8\)

Khi đó phương trình chính tắc của parabol là: \({y^2} = 16x\)

c) Parabol đi qua điểm \(A\left( {4;9} \right) \Rightarrow {9^2} = 2p.4 \Rightarrow 2p = \frac{{81}}{4}\)

Khi đó phương trình chính tắc của parabol là: \({y^2} = \frac{{81}}{4}x\)

Giải bài 1 trang 58 Chuyên đề học tập Toán 10 – Cánh diều

==============

Giải bài 2 trang 59 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Trong mặt phẳng tọa độ Oxy, cho parabol có phương trình chính tắc là \({y^2} = 8x\)

a) Xác định tọa độ tiêu điểm và phương trình đường chuẩn của parabol

b) Vẽ parabol

Phương pháp giải

Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)

+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)

+ Đường chuẩn: \(\Delta : x =  – \frac{p}{2}\)

Lời giải chi tiết

a) Ta có: \(2p = 8 \Rightarrow p = 4\)

Tiêu điểm của parabol (P) là \(F\left( {2;0} \right)\)

Đường chuẩn: \(\Delta : x =  – 2\)

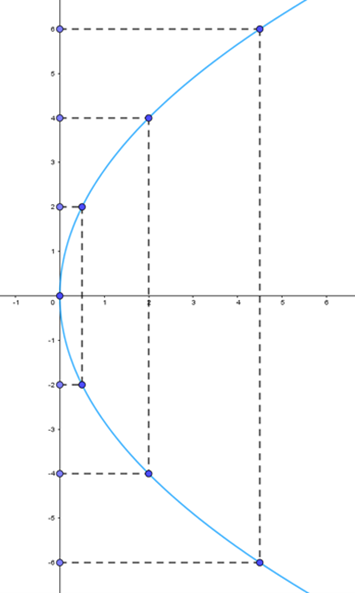
b) Vẽ parabol

Để vẽ parabol (P): \({y^2} = 4x\) ta có thể làm như sau:

Bước 1: Lập bảng giá trị

x	0	0,5	0,5	2	2	4,5	4,5
y	0	-2	2	-4	4	-6	6

Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau

Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị

Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2

 

Giải bài 2 trang 59 Chuyên đề học tập Toán 10 – Cánh diều
=============

Giải bài 3 trang 59 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Các vật liệu xây dựng đều có hệ số dãn nở. Vì thế, khi đặt dầm cầu, người ta thường đặt cố định một đầu dầu, đầu còn lại đặt trên một con lăn có thể di động được nhằm giải quyết sự dãn nở của vật liệu. Hình 21 minh họa một dầm cầu được đặt ở hai bờ kênh, giới hạn bởi hai cung parabol có cùng trục đối xứng. Người ta thiết kế các thanh giằng nối hai cung parabol đó sao cho các thanh giằng theo phương thẳng đứng cách đều nhau và cách đều hai đầu dầm.

Tính tổng độ dài của các thanh giằng theo phương thẳng đứng.

Lời giải chi tiết

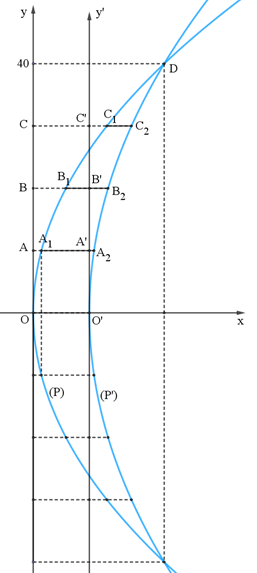
Ta chọn hai hệ trục toạ độ Oxy và O’xy’ sao cho đỉnh của mỗi parabol trùng với O và O’ (như hình vẽ, đơn vị trên các trục là mét).

 

Ta cần tính các đoạn \(OO’,{A_1}{A_2},{B_1}{B_2},{C_1}{C_2}\)

Dễ thấy OO’ = AA’ = BB’ = CC’ = 9.

+ Xét trong hệ trục toạ độ Oxy:

Giả sử parabol (P) có phương trình: \({y^2} = 2px\) trong đó \(p > 0\)

Khi đó D có toạ độ (21; 40) thuộc (P) nên \({40^2} = 2p.21 \Rightarrow 2p = \frac{{1600}}{{21}}\)

Vậy phương trình của (P) là \({y^2} = \frac{{1600}}{{21}}x\).

Với \(y = 10 \Rightarrow x = 1,3125 \Rightarrow A{A_1} = 1,3125\)

Với \(y = 20 \Rightarrow x = 5,25 \Rightarrow B{B_1} = 5,25\)

Với \(y = 30 \Rightarrow x = 11,8125 \Rightarrow C{C_1} = 11,8125\)

+ Xét trong hệ trục toạ độ O’xy’:

Giả sử parabol (P’) có phương trình: \(y{‘^2} = 2px\) trong đó \(p > 0\)

Khi đó D có toạ độ (12; 40) thuộc (P) nên \({40^2} = 2p.12 \Rightarrow 2p = \frac{{400}}{3}\)

Vậy phương trình của (P) là \(y{‘^2} = \frac{{400}}{3}x\).

Với \(y’ = 10 \Rightarrow x = 0,75 \Rightarrow A'{A_1} = 0,75\)

Với \(y’ = 20 \Rightarrow x = 3 \Rightarrow B'{B_1} = 3\)

Với \(y’ = 30 \Rightarrow x = 6,75 \Rightarrow C'{C_1} = 6,75\)

+ Tính các đoạn \(OO’,{A_1}{A_2},{B_1}{B_2},{C_1}{C_2}\):

\({A_1}{A_2} = A{A_2} – A{A_1} = \left( {AA’ + A'{A_2}} \right) – A{A_1} = \left( {9 + 0,75} \right) – 1,3125 = 8,3475\)

Tương tự, ta tính được \({B_1}{B_2} = 6,75;{C_1}{C_2} = 3,9375\)

Tổng độ dài của các thanh giằng theo phương thẳng đứng là: \(OO’ + 2{A_1}{A_2} + 2{B_1}{B_2} + 2{C_1}{C_2} = 9 + 2.8,3475 + 2.6,75 + 2.3,9375 = 47,07\)

Vậy tổng độ dài của các thanh giằng theo phương thẳng đứng là 47,07 mét

 

Giải bài 3 trang 59 Chuyên đề học tập Toán 10 – Cánh diều