Giải Bài 2. Nhị thức Newton – Chuyên đề Toán 10 (Chân trời)

Giải Bài 2. Nhị thức Newton – Chuyên đề Toán 10 (Chân trời)
==========

Giải mục 1 trang 34, 35, 36, 37 Chuyên đề học tập Toán 10

Lựa chọn câu để xem lời giải nhanh hơn

HĐ Khám phá 1

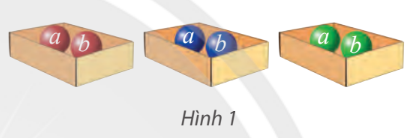
Có ba hộp, mỗi hộp đựng hai quả cầu được dán nhãn a và b (xem Hình 1). Lấy từ mỗi hộp một quả cầu. Có bao nhiêu cách lấy để trong ba quả cầu lấy ra:

a) có 3 quả cầu dán nhãn b?

b) có 2 quả cầu dán nhãn b?

c) có 1 quả cầu dán nhãn b?

d) không có quả cầu nào dán nhãn b?

 

Lời giải chi tiết:

a) Chỉ có 1 cách lấy 3 quả cầu đều là b (bằng \(C_3^3 = 1\))

b) Số cách lấy 2 quả cầu b từ 3 hộp (và 1 quả cầu a từ hộp còn lại) là \(C_3^2 = 3\)

c) Số cách lấy 1 quả cầu b từ 3 hộp (và 2 quả cầu a từ hộp còn lại) là \(C_3^1 = 3\)

d) Chỉ có 1 cách lấy 3 quả cầu mà khoongg có quả cầu b nào (bằng \(C_3^0 = 1\))

Thực hành 1

Hãy khai triển:

a) \({\left( {x – y} \right)^6}\)

b) \({\left( {1 + x} \right)^7}\)

Phương pháp giải:

a) \({(a + b)^6} = C_6^0{a^6} + C_6^1{a^5}b + C_6^2{a^4}{b^2} + C_6^3{a^3}{b^3} + C_6^4{a^2}{b^4} + C_6^5a{b^5} + C_6^6{b^6}\)

b) \({(a + b)^7} = C_7^0{a^7} + C_7^1{a^6}b + C_7^2{a^5}{b^2} + C_7^3{a^4}{b^3} + C_7^4{a^3}{b^4} + C_7^5{a^2}{b^5} + C_7^6a{b^6} + C_7^7{b^7}\)

Lời giải chi tiết:

a) Áp dụng công thức nhị thức Newton, ta có:

\(\begin{array}{l}{(x + ( – y))^6} = C_6^0{x^6} + C_6^1{x^5}( – y) + C_6^2{x^4}{( – y)^2} + C_6^3{x^3}{( – y)^3} + C_6^4{x^2}{( – y)^4} + C_6^5x{( – y)^5} + C_6^6{( – y)^6}\\ = {x^6} + 6{x^5}( – y) + 15{x^4}{( – y)^2} + 20{x^3}{( – y)^3} + 15{x^2}{( – y)^4} + 6x{( – y)^5} + {( – y)^6}\\ = {x^6} – 6{x^5}y + 15{x^4}{y^2} – 20{x^3}{y^3} + 15{x^2}{y^4} – 6x{y^5} + {y^6}\end{array}\)

b) Áp dụng công thức nhị thức Newton, ta có:

\(\begin{array}{l}{(1 + x)^7} = C_7^0{1^7} + C_7^1{1^6}x + C_7^2{1^5}{x^2} + C_7^3{1^4}{x^3} + C_7^4{1^3}{x^4} + C_7^5{1^2}{x^5} + C_7^61.{x^6} + C_7^7{x^7}\\ = 1 + 7x + 21{x^2} + 35{x^3} + 35{x^4} + 21{x^5} + 7{x^6} + {x^7}\end{array}\)

Giải mục 2 trang 35, 36, 37 Chuyên đề học tập Toán 10

Lựa chọn câu để xem lời giải nhanh hơn

HĐ Khám phá 2

Từ các đẳng thức như

\(\begin{array}{l}C_3^0 = C_3^3 = 1,\quad C_4^1 = C_4^3 = 4,\\C_3^0 + C_3^1 = C_4^1,\quad C_4^2 + C_4^3 = C_5^3,\end{array}\)

Có thể dự đoán rằng, với mỗi \(n \in \mathbb{N}*\),

\(\begin{array}{l}C_n^k = C_n^{n – k}\quad \quad \quad (0 \le k \le n)\quad (2)\\C_n^{k – 1} + C_n^k = C_{n + 1}^k\quad (1 \le k \le n)\quad (3)\end{array}\)

Hãy chứng minh các công thức trên.

Gợi ý: Sử dụng công thức \(C_n^k = \frac{{n!}}{{k!\left( {n – k} \right)!}},n \in \mathbb{N},0 \le k \le n.\)

Lời giải chi tiết:

\(C_n^k = \frac{{n!}}{{k!\left( {n – k} \right)!}} = \frac{{n!}}{{\left( {n – k} \right)!k!}} = \frac{{n!}}{{\left( {n – k} \right)!\left[ {n – (n – k)} \right]!}} = C_n^{n – k}\)

\(\begin{array}{l}C_n^{k – 1} + C_n^k = \frac{{n!}}{{(k – 1)!\left( {n – k + 1} \right)!}} + \frac{{n!}}{{k!\left( {n – k} \right)!}}\\ = \frac{{n!}}{{k!\left( {n + 1 – k} \right)!}}\left( {k + \left( {n + 1 – k} \right)} \right)\\ = \frac{{(n + 1)!}}{{k!\left( {n + 1 – k} \right)!}} = C_{n + 1}^k\end{array}\)

Thực hành 2

Sử dụng tam giác Pascal, hãy khai triển:

a) \({(2x + 1)^6}\)

b) \({(x – y)^7}\)

Phương pháp giải:

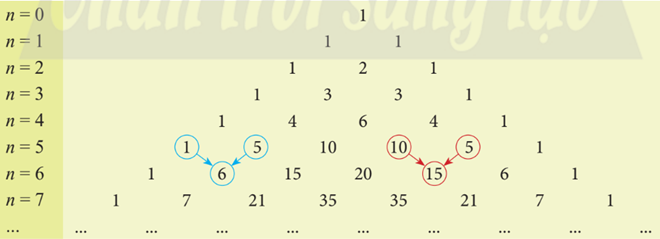
Lời giải chi tiết:

a) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(2x + 1)^6} = {\left( {2x} \right)^6} + 6{\left( {2x} \right)^5} + 15{\left( {2x} \right)^4} + 20{\left( {2x} \right)^3} + 15{\left( {2x} \right)^2} + 6.2x + 1\\ = 64{x^6} + 192{x^5} + 240{x^4} + 160{x^3} + 60{x^2} + 12x + 1\end{array}\)

b) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(x + ( – y))^7} = {x^7} + 7{x^6}( – y) + 21{x^5}{( – y)^2} + 35{x^4}{( – y)^3} + 35{x^3}{( – y)^4} + 21{x^2}{( – y)^5} + 7x{( – y)^6} + {( – y)^7}\\ = {x^7} – 7{x^6}y + 21{x^5}{y^2} – 35{x^4}{y^3} + 35{x^3}{y^4} – 21{x^2}{y^5} + 7x{y^6} – {y^7}\end{array}\)

 

Giải mục 3 trang 37, 38 Chuyên đề học tập Toán 10

Lựa chọn câu để xem lời giải nhanh hơn

Thực hành 3

Xác định hệ số của \({x^2}\) trong khai triển của \({(3x + 2)^9}\)

Phương pháp giải:

Công thức nhị thức Newton: \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Số hạng chứa \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{(ax)^k}{b^{n – k}}\)

Do đó hệ số của \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{a^k}{b^{n – k}}\)

Lời giải chi tiết:

Theo công thức nhị thức Newton, ta có:

\({(3x + 2)^9} = C_9^0{\left( {3x} \right)^9} + C_9^1{\left( {3x} \right)^8}2 + … + C_9^k{\left( {3x} \right)^{9 – k}}{2^k} + … + C_9^8\left( {3x} \right){2^8} + C_9^9{2^9}\)

Số hạng chứa \({x^2}\) ứng với \(9 – k = 2\) hay \(k = 7\). Do đó hệ số của \({x^2}\)  là

\(C_9^7{3^2}{2^7} = 36.9.128 = 41472\)

Thực hành 4

Biết rằng trong khai triển của \({(x + a)^6}\) với a là một số thực, hệ số của \({x^4}\) là 60. Tìm giá trị của a.

Phương pháp giải:

Công thức nhị thức Newton: \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Số hạng chứa \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{(ax)^k}{b^{n – k}}\)

Do đó hệ số của \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{a^k}{b^{n – k}}\)

Lời giải chi tiết:

Áp dụng công thức nhị thức Newton, ta có:

\({(x + a)^6} = C_6^0{x^6} + C_6^1{x^5}a + … + C_6^k{x^{6 – k}}{a^k} + … + C_6^6{a^6}\)

Số hạng chứa \({x^4}\) ứng với \(6 – k = 4\) hay \(k = 2\). Hệ số của số hạng chứa \({x^4}\)  là \(C_6^2{a^2}\)

Theo giả thiết ta có: \(C_6^2{a^2} = 60\)

\( \Leftrightarrow 15{a^2} = 60 \Leftrightarrow {a^2} = 4 \Leftrightarrow \left[ \begin{array}{l}a = 2\\a =  – 2\end{array} \right.\)

Vậy \(a = 2\) hoặc \(a =  – 2\).

Thực hành 5

Chứng minh rằng, với mọi \(n \in \mathbb{N}*\), ta có

\(C_n^0 – C_n^1 + C_n^2 – C_n^3 + … + {\left( { – 1} \right)^n}C_n^n = 0\)

Phương pháp giải:

Công thức nhị thức Newton: \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Lời giải chi tiết:

Áp dụng công thức nhị thức Newton, ta có:

\({(1 + x)^n} = C_n^0 + C_n^1x + C_n^2{x^2} + … + C_n^n{x^n}\)

Thay \(x =  – 1\) ta được:

\(0 = C_n^0 + ( – 1)C_n^1 + {( – 1)^2}C_n^2 + {( – 1)^3}C_n^3 + … + {\left( { – 1} \right)^n}C_n^n\)

Hay \(C_n^0 – C_n^1 + C_n^2 – C_n^3 + … + {\left( { – 1} \right)^n}C_n^n = 0\)

Vận dụng

Trong hộp A có 10 quả cầu được đánh số từ 1 đến 10. Người ta lấy một số quả cầu từ hộp A rồi cho vào hộp B. Có tất cả bao nhiêu cách lấy, tính cả trường hợp lấy 0 quả (tức là không lấy quả nào)?

Phương pháp giải:

Công thức nhị thức Newton: \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Lời giải chi tiết:

Giả sử lấy k quả cầu từ hộp A cho sáng hộp B. \((0 \le k \le 10)\)

Để lấy k quả cầu, có \(C_{10}^k\) cách lấy. (trường hợp không lấy quả nào được tính là 1 cách, bằng \(C_{10}^0\))

Vậy số cách lấy một số quả cầu (kể cả cách lấy 0 quả) từ hộp A cho sang hộp B là:

\(C_{10}^0 + C_{10}^1 + C_{10}^2 + … + C_{10}^{10} = {2^{10}} = 1024.\)

 

Giải bài 1 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Khai triển biểu thức:

a) \({(x – 2y)^6}\)

b) \({(3x – 1)^5}\)

Sử dụng công thức nhị thức Newton

\({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

hoặc tam giác Pascal

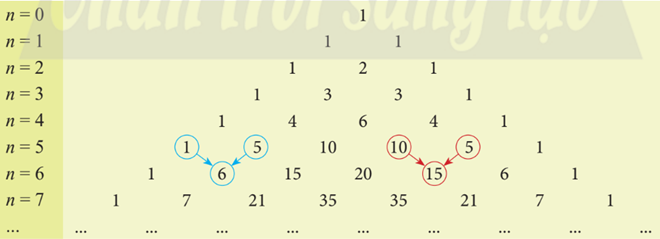
Lời giải chi tiết

a) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(x + ( – 2y))^6} = {x^6} + 6{x^5}( – 2y) + 15{x^4}{( – 2y)^2} + 20{x^3}{( – 2y)^3} + 15{x^2}{( – 2y)^4} + 6x{( – 2y)^5} + {( – 2y)^6}\\ = {x^6} – 12{x^5}y + 60{x^4}{y^2} – 160{x^3}{y^3} + 240{x^2}{y^4} – 192x{y^5} + 64{y^6}\end{array}\)

b) Sử dụng tam giác Pascal, ta có:

\(\begin{array}{l}{(3x – 1)^5} = {\left( {3x} \right)^5} + 5.{\left( {3x} \right)^4}( – 1) + 10.{\left( {3x} \right)^3}{( – 1)^2} + 10.{\left( {3x} \right)^2}{( – 1)^3} + 5.\left( {3x} \right){( – 1)^4} + {( – 1)^5}\\ = 243{x^5} – 405{x^4} + 270{x^3} – 90{x^2} + 15x – 1\end{array}\)

 

Giải bài 2 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Tìm hệ số của \({x^{10}}\) trong khai triển của biểu thức \({(2 – x)^{12}}\)

Công thức nhị thức Newton: \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Lời giải chi tiết

Theo công thức nhị thức Newton, ta có:

\(\begin{array}{l}{(2 – x)^{12}} = C_{12}^0{2^{12}} + C_{12}^1{2^{11}}\left( { – x} \right) + … + C_{12}^k{2^{12 – k}}{\left( { – x} \right)^k} + … + C_{12}^{12}{( – x)^{12}}\\ = C_{12}^0{2^{12}} – C_{12}^1{2^{11}}x + … + {( – 1)^k}C_{12}^k{2^{12 – k}}{x^k} + … + C_{12}^{12}{x^{12}}\end{array}\)

Số hạng chứa \({x^{10}}\) ứng với \(k = 10\). Do đó hệ số của \({x^{10}}\)  là

\(C_{12}^{10}{2^2}{( – 1)^{10}} = 66.4.1 = 264\)

Giải bài 3 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Biết rằng a là một số thực khác 0 và trong khai triển của \({(ax + 1)^6}\), hệ số của \({x^4}\) gấp 4 lần hệ số của \({x^4}\). Tìm giá trị của a.

Công thức nhị thức Newton: \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Số hạng chứa \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{(ax)^k}{b^{n – k}}\)

Do đó hệ số của \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{a^k}{b^{n – k}}\)

Lời giải chi tiết

Áp dụng công thức nhị thức Newton, ta có:

\({(ax + 1)^6} = C_6^0{\left( {ax} \right)^6} + C_6^1{\left( {ax} \right)^5} + … + C_6^k{\left( {ax} \right)^{6 – k}} + … + C_6^6\)

Số hạng chứa \({x^4}\) ứng với \(6 – k = 4\) hay \(k = 2\). Hệ số của số hạng chứa \({x^4}\)  là \(C_6^2{a^4}\)

Số hạng chứa \({x^2}\) ứng với \(6 – k = 2\) hay \(k = 4\). Hệ số của số hạng chứa \({x^2}\)  là \(C_6^4{a^2}\)

Theo giả thiết ta có: \(C_6^2{a^4} = 4C_6^4{a^2} \Leftrightarrow 15{a^4} = 4.15{a^2} \Leftrightarrow {a^2} = 4\) (do \(a \ne 0\))\( \Leftrightarrow \left[ \begin{array}{l}a = 2\\a =  – 2\end{array} \right.\)

Vậy \(a = 2\) hoặc \(a =  – 2\).

Giải bài 4 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Biết hệ số của \({x^2}\) trong khai triển của \({(1 + 3x)^n}\) là 90. Tìm giá trị của n.

Số hạng chứa \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{(ax)^k}{b^{n – k}}\)

Do đó hệ số của \({x^k}\) trong khai triển của \({(ax + b)^n}\) là \(C_n^{n – k}{a^k}{b^{n – k}}\)

Lời giải chi tiết

Áp dụng công thức nhị thức Newton, ta có:

\({(1 + 3x)^n} = C_n^0 + C_n^1\left( {3x} \right) + … + C_n^k{\left( {3x} \right)^k} + … + C_n^n{\left( {3x} \right)^n}\)

Số hạng chứa \({x^2}\) ứng với \(k = 2\), tức là số hạng \(C_n^2{(3x)^2}\). Do đó hệ số là \(9.C_n^2\)

Do đó \(9.C_n^2 = 90 \Leftrightarrow C_n^{n – 2} = 10 \Leftrightarrow \frac{{n!}}{{2!(n – 2)!}} = 10\)

 \( \Leftrightarrow \frac{{n(n – 1)}}{2} = 10 \Leftrightarrow {n^2} – n – 20 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n =  – 4\;(L)\end{array} \right.\)

Vậy \(n = 5\) thì hệ số của \({x^2}\) trong khai triển của \({(1 + 3x)^n}\) là 90.

Giải bài 5 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Chứng minh công thức nhị thức Newton (công thức (1) trang 35) bằn phương pháp quy nạp toán học.

Chứng minh mệnh đề đúng với \(n \ge p\) thì:

Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)

Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.

Lời giải chi tiết

Công thức nhị thức Newton: \({(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … + C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}\)

Ta chứng minh công thức nhị thức Newton bằng quy nạp theo n.

Bước 1: Với \(n = 1\) ta có \({(a + b)^1} = C_1^0a + C_1^1b\quad ( = a + b)\)

Như vậy công thức đúng cho trường hợp \(n = 1\)

Bước 2: Giả sử công thức đúng với \(n = k\), nghĩa là có:

\({(a + b)^k} = C_k^0{a^k} + C_k^1{a^{k – 1}}b + … + C_k^{k – 1}a{b^{k – 1}} + C_k^k{b^k}\)

Ta sẽ chứng minh công thức cũng đúng với \(n = k + 1\), nghĩa là cần chứng minh

\({(a + b)^{k + 1}} = C_{k + 1}^0{a^{k + 1}} + C_{k + 1}^1{a^k}b + … + C_{k + 1}^ka{b^k} + C_{k + 1}^{k + 1}{b^{k + 1}}\)

Thật vậy ta có

\(\begin{array}{l}{(a + b)^{k + 1}} = {(a + b)^k}(a + b) = \left( {C_k^0{a^k} + C_k^1{a^{k – 1}}b + … + C_k^{k – 1}a{b^{k – 1}} + C_k^k{b^k}} \right)(a + b)\\ = \left( {C_k^0{a^k} + C_k^1{a^{k – 1}}b + … + C_k^{k – 1}a{b^{k – 1}} + C_k^k{b^k}} \right)a + \left( {C_k^0{a^k} + C_k^1{a^{k – 1}}b + … + C_k^{k – 1}a{b^{k – 1}} + C_k^k{b^k}} \right)b\\ = \left( {C_k^0{a^{k + 1}} + C_k^1{a^k}b + … + C_k^{k – 1}{a^2}{b^{k – 1}} + C_k^ka{b^k}} \right) + \left( {C_k^0{a^k}b + C_k^1{a^{k – 1}}{b^2} + … + C_k^{k – 1}a{b^k} + C_k^k{b^{k + 1}}} \right)\\ = C_k^0{a^{k + 1}} + \left( {C_k^1 + C_k^0} \right){a^k}b + … + \left( {C_k^m + C_k^{m – 1}} \right){a^{k + 1 – m}}{b^m} + … + \left( {C_k^k + C_k^{k – 1}} \right)a{b^k} + C_k^k{b^{k + 1}}\end{array}\)

Mà \(C_k^m + C_k^{m – 1} = C_{k + 1}^m\;(0 \le m \le k),\;C_k^0 = C_{k + 1}^0 = 1,C_k^k = C_{k + 1}^{k + 1} = 1\)

\( \Rightarrow {(a + b)^{k + 1}} = C_{k + 1}^0{a^{k + 1}} + C_{k + 1}^1{a^k}b + … + C_{k + 1}^ka{b^k} + C_{k + 1}^{k + 1}{b^{k + 1}}\)

Vậy công thức đúng với mọi số tự nhiên \(n \ge 1\)

 

Giải bài 6 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Biết rằng \({(3x – 1)^7} = {a_0} + {a_1}x + {a_2}{x^2} + … + {a_7}{x^7}\). Hãy tính:

a) \({a_0} + {a_1} + {a_2} + … + {a_7}\)

b) \({a_0} + {a_2} + {a_4} + {a_6}\)

Lời giải chi tiết

Ta có:

\({(3x – 1)^7} = {a_0} + {a_1}x + {a_2}{x^2} + … + {a_7}{x^7}\)

a) Thay \(x = 1\) vào công thức khai triển trên ta được:

\({a_0} + {a_1} + {a_2} + … + {a_7} = {(3.1 – 1)^7} = {2^7} = 128\)

b) Thay \(x =  – 1\) vào công thức khai triển trên ta được:

\({a_0} – {a_1} + {a_2} – .. – {a_7} = {(3.( – 1) – 1)^7} = {( – 4)^7} =  – 16384\)

Cộng vế với vế đẳng thức trên và đẳng thức ở a), ta được:

\(\begin{array}{l}2\left( {{a_0} + {a_2} + {a_4} + {a_6}} \right) = 128 + ( – 16384) =  – 16256\\ \Rightarrow {a_0} + {a_2} + {a_4} + {a_6} =  – 8128\end{array}\)

Giải bài 7 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Mỗi tập hợp có 12 phần tử thì có tất cả bao nhiêu tập hợp con?

Lời giải chi tiết

Lời giải chi tiết

Cách 1:

Số tập hợp con có 0 phần tử là: \(1 = C_{12}^0\) (tập rỗng)

Số tập hợp con có 1 phần tử là: \(C_{12}^1\)

Số tập hợp con có k phần tử là: \(C_{12}^k\)

\( \Rightarrow \)Số tập hợp con của tập hợp có 12 phần tử là: \(C_{12}^0 + C_{12}^1 + C_{12}^2 + … + C_{12}^{12}\)

Theo công thức nhị thức Newton, ta có:

\({\left( {1 + x} \right)^{12}} = C_{12}^0 + C_{12}^1x + C_{12}^2{x^2} + … + C_{12}^{12}{x^{12}}\)

Thay \(x = 1\) ta được \(C_{12}^0 + C_{12}^1 + C_{12}^2 + … + C_{12}^{12} = {2^{12}} = 4096\)

Cách 2:

Ta chứng minh bằng quy nạp công thức: Tập hợp A có n phần tử thì có \({2^n}\) tập con.

Bước 1: Với \(n = 0\) ta có A là tập rỗng có duy nhất \(1 = {2^0}\) tập con là tập rỗng.

Như vậy mệnh đề đúng cho trường hợp \(n = 0\)

Bước 2: Giả sử mệnh đề đúng với \(n = k\), nghĩa là có:

Tập hợp A có k phần tử thì có \({2^k}\) tập con

Ta sẽ chứng minh mệnh đề cũng đúng với \(n = k + 1\), nghĩa là cần chứng minh

Tập hợp A có \(k + 1\) phần tử thì có \({2^{k + 1}}\) tập con

Thật vậy chọn ra k phần tử của A, từ đó tạo thành \({2^k}\) tập con theo giả thiết quy nạp. Ngoài ra, với mỗi tập trong  \({2^k}\)tập này, ta bổ sung thêm phần tử thứ k+1 còn lại vào mỗi tập. Ta thu được thêm \({2^k}\)tập nữa. Do đó ta được tất cả \({2^k} + {2^k} = {2.2^k} = {2^{k + 1}}\) tập con

Vậy mệnh đề đúng với mọi số tự nhiên \(n \in \mathbb{N}\)

Như vậy tập có 12 phần tử thì có tất cả \({2^{12}} = 4096\) tập con.

 

Giải bài 8 trang 39 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Từ 15 bút chì màu có màu khác nhau đôi một,

a) Có bao nhiêu cách chọn ra một số bút chì màu, tính cả trường trường hợp hợp không chọn cái nào?

b) Có bao nhiêu cách chọn ra ít nhất 8 bút chì màu?

Lời giải chi tiết

a)

Số cách chọn ra 0 bút chì màu là: \(1 = C_{15}^0\) (Không chọn cái nào là 1 cách)

Số cách chọn ra 1 bút chì màu là: \(C_{15}^1\)

Số cách chọn ra k bút chì màu là: \(C_{15}^k\)

\( \Rightarrow \)Tổng số cách chọn ra một số bút chì màu là: \(C_{15}^0 + C_{15}^1 + C_{15}^2 + … + C_{15}^{15}\)

Theo công thức nhị thức Newton, ta có:

\({\left( {1 + x} \right)^{15}} = C_{15}^0 + C_{15}^1x + C_{15}^2{x^2} + … + C_{15}^{15}{x^{15}}\)

Thay \(x = 1\) ta được \(C_{15}^0 + C_{15}^1 + C_{15}^2 + … + C_{15}^{15} = {2^{15}} = 32768\)

Vậy có 32768 cách chọn ra một số bút chì màu, tính cả trường hợp không chọn cái nào.

b) Số cách chọn ra k bút chì màu là: \(C_{15}^k\)

\( \Rightarrow \)Tổng số cách chọn ra ít nhất 8 bút chì màu là: \(C_{15}^8 + C_{15}^9 + C_{15}^{10} + … + C_{15}^{15}\)

Mà \(C_{15}^k = C_{15}^{15 – k},0 \le k \le 15\)

\(\begin{array}{l} \Rightarrow C_{15}^8 + C_{15}^9 + C_{15}^{10} + … + C_{15}^{15} = C_{15}^7 + C_{15}^6 + C_{15}^5 + … + C_{15}^0\\\frac{1}{2}\left( {C_{15}^0 + C_{15}^1 + C_{15}^2 + … + C_{15}^{15}} \right) = \frac{1}{2}{.2^{15}} = 16384\end{array}\)

Vậy có 16384 cách chọn ra ít nhất 8 bút chì màu.