ĐỀ THAM KHẢO THI HK2 môn TOÁN LỚP 12 (2022) – ĐỀ 5

Câu 2:

Cho hai hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(a < c < b\). Mệnh đề nào dưới đây sai?

• A.
  \(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx = \int\limits_a^b {f\left( x \right)dx}  + \int\limits_a^b {g\left( x \right)dx} } \) 
• B.
  \(\int\limits_a^b {k.f\left( x \right)dx = } k.\int\limits_a^b {f\left( x \right)dx} \)với \(k\) là hằng số 
• C.
  \(\int\limits_a^b {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}dx}  = \dfrac{{\int\limits_a^b {f\left( x \right)dx} }}{{\int\limits_a^b {g\left( x \right)dx} }}\) 
• D.
  \(\int\limits_a^b {f\left( x \right)dx}  = \int\limits_a^c {f\left( x \right)dx}  + \int\limits_c^b {f\left( x \right)dx} \) 

Câu 3:

Gọi \(S\) là diện tích của hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right),y = g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và các đường thẳng \(x = a,x = b\). Diện tích \(S\) được tính theo công thức nào dưới đây? 

• A.
  \(S = \int\limits_a^b {\left[ {g\left( x \right) – f\left( x \right)} \right]dx} \) 
• B.
  \(S = \int\limits_a^b {\left| {f\left( x \right) – g\left( x \right)} \right|dx} \) 
• C.
  \(S = \left| {\int\limits_a^b {\left[ {f\left( x \right) – g\left( x \right)} \right]dx} } \right|\) 
• D.
  \(S = \int\limits_a^b {\left[ {f\left( x \right) – g\left( x \right)} \right]dx} \) 

Câu 4:

Trong không gian \(Oxyz\), gọi \(\varphi \) là góc tạo bởi hai vecto \(\overrightarrow a  = \left( {3; – 1;2} \right)\) và \(\overrightarrow b  = \left( {1;1; – 1} \right)\). Mệnh đề nào dưới đây đúng? 

• A.
  \(\varphi  = 30^\circ \) 
• B.
  \(\varphi  = 45^\circ \) 
• C.
  \(\varphi  = 90^\circ \) 
• D.
  \(\varphi  = 60^\circ \) 

Câu 5:

Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {1;3} \right]\), \(F\left( 1 \right) = 3,F\left( 3 \right) = 5\) và \(\int\limits_1^3 {\left( {{x^4} – 8x} \right)f\left( x \right)dx}  = 12\). Tính \(I = \int\limits_1^3 {\left( {{x^3} – 2} \right)F\left( x \right)dx} \). 

• A.
  \(I = \dfrac{{147}}{2}\) 
• B.
  \(I = \dfrac{{147}}{3}\) 
• C.
  \(I =  – \dfrac{{147}}{2}\) 
• D.
  \(I = 147\) 

Câu 6:

Trong không gian \(Oxyz\), cho đường thẳng \(d:\dfrac{{x – 3}}{2} = \dfrac{{y – 1}}{{ – 1}} = \dfrac{{z + 5}}{3}\). Tìm tọa độ một véc tơ chỉ phương của đường thẳng \(d.\) 

• A.
  \(\overrightarrow a  = \left( {2; – 1;3} \right)\) 
• B.
  \(\overrightarrow b  = \left( {2;1;3} \right)\) 
• C.
  \(\overrightarrow u  = \left( {3;1; – 5} \right)\) 
• D.
  \(\overrightarrow q  = \left( { – 3;1;5} \right)\) 

Câu 7:

Biết \(\int\limits_1^3 {f\left( x \right)dx}  = 9,\int\limits_1^3 {g\left( x \right)dx}  =  – 5\). Tính \(K = \int\limits_1^3 {\left[ {2f\left( x \right) – 3g\left( x \right)} \right]dx} \). 

• A.
  \(K = 3\) 
• B.
  \(K = 33\) 
• C.
  \(K = 4\) 
• D.
  \(K = 14\) 

Câu 8:

Biết \(\int {f\left( t \right)dt}  = {t^2} + 3t + C.\) Tính \(\int {f\left( {\sin 2x} \right)\cos 2xdx} \) 

• A.
  \(\int {f\left( {\sin 2x} \right)\cos 2xdx}  = 2{\sin ^2}x + 6\sin x + C\) 
• B.
  \(\int {f\left( {\sin 2x} \right)\cos 2xdx}  = 2{\sin ^2}2x + 6\sin 2x + C\) 
• C.
  \(\int {f\left( {\sin 2x} \right)\cos 2xdx}  = \dfrac{1}{2}{\sin ^2}2x + \dfrac{3}{2}\sin 2x + C\) 
• D.
  \(\int {f\left( {\sin 2x} \right)\cos 2xdx}  = {\sin ^2}2x + 3\sin 2x + C\) 

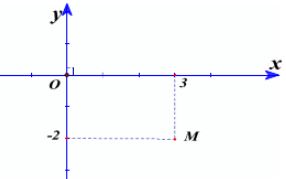
Câu 9:

Điểm \(M\) trong hình vẽ bên là điểm biểu diễn của số phức nào dưới đây?

• A.
  \(z =  – 2 + 3i\) 
• B.
  \(z = 3 + 2i\) 
• C.
  \(z = 2 – 3i\) 
• D.
  \(z = 3 – 2i\) 

Câu 10:

Tìm số phức \(\overline z \) , biết \(\left( {2 – 5i} \right)z – 3 + 2i = 5 + 7i\).

• A.
  \(\overline z  =  – \dfrac{9}{{29}} + \dfrac{{50}}{{29}}i\) 
• B.
  \(\overline z  =  – \dfrac{9}{{29}} – \dfrac{{50}}{{29}}i\) 
• C.
  \(\overline z  = \dfrac{9}{{29}} – \dfrac{{50}}{{29}}i\) 
• D.
  \(\overline z  = \dfrac{9}{{29}} + \dfrac{{50}}{{29}}i\) 

Câu 11:

Gọi \({z_1},{z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 3 = 0\) . Tính \(P = 2\left| {{z_1}} \right| + 5\left| {{z_2}} \right|\). 

• A.
  \(P = \sqrt 3 \) 
• B.
  \(P = 5\sqrt 3 \) 
• C.
  \(P = 3\sqrt 3 \) 
• D.
  \(P = 7\sqrt 3 \) 

Câu 12:

Cho hai số phức \({z_1} = 3 – 4i\) và \({z_2} =  – 2 + i\). Tìm số phức liên hợp của \({z_1} + {z_2}.\) 

• A.
  \(1 + 3i\)
• B.
  \(1 – 3i\) 
• C.
  \( – 1 + 3i\) 
• D.
  \( – 1 – 3i\) 

Câu 13:

Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \dfrac{1}{{2x + 3}}\) và \(F\left( 0 \right) = 0\). Tính \(F\left( 2 \right)\). 

• A.
  \(F\left( 2 \right) = \ln \dfrac{7}{3}\) 
• B.
  \(F\left( 2 \right) =  – \dfrac{1}{2}\ln 3\) 
• C.
  \(F\left( 2 \right) = \dfrac{1}{2}\ln \dfrac{7}{3}\) 
• D.
  \(F\left( 2 \right) = \ln 21\) 

Câu 14:

Trong không gian \(Oxyz\), cho điểm \(A\left( {3;5;2} \right)\). Phương trình nào dưới đây là phương trình mặt phẳng đi qua các điểm là hình chiếu của điểm \(A\) trên các mặt phẳng tọa độ? 

• A.
  \(10x + 6y + 15z – 90 = 0\) 
• B.
  \(10x + 6y + 15z – 60 = 0\) 
• C.
  \(3x + 5y + 2z – 60 = 0\) 
• D.
  \(\dfrac{x}{3} + \dfrac{y}{5} + \dfrac{z}{2} = 1\) 

Câu 15:

Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\). Mệnh đề nào dưới đây đúng? 

• A.
  \(\int\limits_a^b {f\left( x \right)dx}  = F\left( a \right) – F\left( b \right)\) 
• B.
  \(\int\limits_a^b {f\left( x \right)dx}  = F\left( b \right) – F\left( a \right)\) 
• C.
  \(\int\limits_a^b {f\left( x \right)dx}  = F\left( b \right) + F\left( a \right)\) 
• D.
  \(\int\limits_a^b {f\left( x \right)dx}  = F’\left( b \right) – F’\left( a \right)\) 

Câu 16:

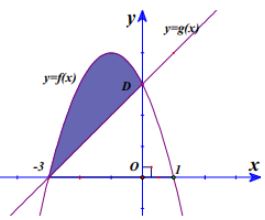
Cho hình phẳng \(D\) giới hạn bởi đồ thị của hai hàm số \(y = f\left( x \right),y = g\left( x \right)\) (phần tô đậm trong hình vẽ). Gọi \(S\) là diện tích của hình phẳng \(D\). Mệnh đề nào dưới đây đúng?

• A.
  \(S = \int\limits_{ – 3}^0 {\left[ {f\left( x \right) – g\left( x \right)} \right]dx} \) 
• B.
  \(S = \int\limits_{ – 3}^0 {\left[ {g\left( x \right) – f\left( x \right)} \right]dx} \) 
• C.
  \(S = \int\limits_{ – 3}^0 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} \) 
• D.
  \(S = \int\limits_{ – 3}^1 {{{\left[ {f\left( x \right) – g\left( x \right)} \right]}^2}dx} \) 

Câu 17:

Tìm phần thực \(a\) và phần ảo \(b\) của số phức \(z = \sqrt 5  – 2i\). 

• A.
  \(a =  – 2,b = \sqrt 5 \) 
• B.
  \(a = \sqrt 5 ,b = 2\) 
• C.
  \(a = \sqrt 5 ,b =  – 2\) 
• D.
  \(a = \sqrt 5 ,b =  – 2i\) 

Câu 18:

Gọi D là phần hình phảng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right],\) trục hoành và hai đường thẳng \(x = a;x = b.\) Thể tích \(V\) của khối tròn xoay tạo thành khi quay hình D xung quanh trục \(Ox\) được tính theo công thức nào dưới đây? 

• A.
  \(V = {\pi ^2}\int\limits_a^b {f\left( x \right)dx} \) 
• B.
  \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \) 
• C.
  \(V = {\left( {\pi \int\limits_a^b {f\left( x \right)dx} } \right)^2}\) 
• D.
  \(V = 2\pi \int\limits_a^b {{f^2}\left( x \right)dx} \) 

Câu 19:

Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \sin 2x\) và \(F\left( {\dfrac{\pi }{4}} \right) =  – 1\). Tính \(F\left( {\dfrac{\pi }{6}} \right)\). 

• A.
  \(F\left( {\dfrac{\pi }{6}} \right) = \dfrac{5}{4}\) 
• B.
  \(F\left( {\dfrac{\pi }{6}} \right) =  – \dfrac{{\sqrt 3 }}{4} – 1\) 
• C.
  \(F\left( {\dfrac{\pi }{6}} \right) = \sqrt 3  – 1\) 
• D.
  \(F\left( {\dfrac{\pi }{6}} \right) =  – \dfrac{5}{4}\) 

Câu 20:

Trên mặt phẳng tọa dộ, tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn \(\left| z \right| = \sqrt 7 .\) 

• A.
  Đường tròn tâm \(O\left( {0;0} \right)\) , bán kính \(R = \dfrac{7}{2}.\)  
• B.
  Đường tròn tâm \(O\left( {0;0} \right)\), bán kính \(R = 7\) 
• C.
  Đường tròn tâm \(O\left( {0;0} \right),\) bán kính \(R = 49\) 
• D.
  Đường tròn tâm \(O\left( {0;0} \right)\), bán kính \(R = \sqrt 7 \) 

Câu 21:

Trong không gian \(Oxyz\), cho tam giác \(ABC\) biết \(C\left( {1;1;1} \right)\) và trọng tâm \(G\left( {2;5;8} \right)\). Tìm tọa độ các đỉnh \(A\) và \(B\) biết \(A\) thuộc mặt phẳng \(\left( {Oxy} \right)\) và \(B\) thuộc trục \(Oz\). 

• A.
  \(A\left( {3;9;0} \right)\)và \(B\left( {0;0;15} \right)\) 
• B.
  \(A\left( {6;15;0} \right)\)và \(B\left( {0;0;24} \right)\) 
• C.
  \(A\left( {7;16;0} \right)\)và \(B\left( {0;0;25} \right)\) 
• D.
  \(A\left( {5;14;0} \right)\)và \(B\left( {0;0;23} \right)\) 

Câu 22:

Cho số phức \({z_1} = 1 – 2i\) và \({z_2} = 3 + 4i.\) Tìm điểm \(M\) biểu diễn số phức \({z_1}.{z_2}\) trên mặt phẳng tọa độ. 

• A.
  \(M\left( { – 2;11} \right)\) 
• B.
  \(M\left( {11;2} \right)\) 
• C.
  \(M\left( {11; – 2} \right)\) 
• D.
  \(M\left( { – 2; – 11} \right)\) 

Câu 23:

Trong không gian Oxyz, tìm tọa độ của vectơ \(\overrightarrow a \) biết \(\overrightarrow a  = 3\overrightarrow i  – 5\overrightarrow k \). 

• A.
  \(\overrightarrow a  = \left( {0;3; – 5} \right)\) 
• B.
  \(\overrightarrow a  = \left( {3;0;5} \right)\) 
• C.
  \(\overrightarrow a  = \left( {3; – 5;0} \right)\) 
• D.
  \(\overrightarrow a  = \left( {3;0; – 5} \right)\) 

Câu 24:

Tính \(\int {{3^{2018x}}dx} \) 

• A.
  \(\int {{3^{2018x}}dx}  = \dfrac{{{3^{2018x}}}}{{\ln 3}} + C\) 
• B.
  \(\int {{3^{2018x}}dx}  = \dfrac{{{3^{2018x}}}}{{\ln 2018}} + C\) 
• C.
  \(\int {{3^{2018x}}dx}  = \dfrac{{{3^{2018x}}}}{{2018\ln 3}} + C\) 
• D.
  \(\int {{3^{2018x}}dx}  = \dfrac{{{3^{2018x}}}}{{2019}} + C\) 

Câu 25:

Tính môđun của số phức \(z\) thỏa mãn \(\left( {1 + i} \right)z\left| z \right| – 1 = \left( {i – 2} \right)\left| z \right|\). 

• A.
  \(\left| z \right| = 1\) 
• B.
  \(\left| z \right| = 4\) 
• C.
  \(\left| z \right| = 2\) 
• D.
  \(\left| z \right| = 3\) 

Câu 26:

Biết \(F\left( x \right) =  – \dfrac{1}{{{x^2}}}\) là một nguyên hàm của hàm số \(y = \dfrac{{f\left( x \right)}}{x}.\) Tính \(\int {f’\left( x \right)\ln xdx.} \) 

• A.
  \(\int {f’\left( x \right)\ln xdx}  =  – \dfrac{{2\ln x}}{{{x^2}}} + \dfrac{1}{{{x^2}}} + C\) 
• B.
  \(\int {f’\left( x \right)\ln xdx}  = \dfrac{{2\ln x}}{{{x^2}}} + \dfrac{1}{{{x^2}}} + C\) 
• C.
  \(\int {f’\left( x \right)\ln xdx}  = \dfrac{{2\ln x}}{{{x^2}}} – \dfrac{1}{{{x^2}}} + C\) 
• D.
  \(\int {f’\left( x \right)\ln xdx}  =  – \dfrac{{2\ln x}}{{{x^2}}} – \dfrac{1}{{{x^2}}} + C\) 

Câu 27:

Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = \cos x + 2\), trục hoành và các đường thẳng \(x = 0,x = \dfrac{\pi }{4}\). 

• A.
  \(S = \dfrac{\pi }{2} – \dfrac{{\sqrt 2 }}{2}\) 
• B.
  \(S = \dfrac{\pi }{4} + \dfrac{7}{{10}}\) 
• C.
  \(S = \dfrac{\pi }{2} + \dfrac{{\sqrt 2 }}{2}\) 
• D.
  \(S = \dfrac{\pi }{4} + \dfrac{{\sqrt 2 }}{2}\) 

Câu 28:

Tìm tọa độ của điểm biểu diễn số phức \(z = \dfrac{{3 + 4i}}{{1 – i}}\) trên mặt phẳng tọa độ. 

• A.
  \(Q\left( {\dfrac{1}{2}; – \dfrac{7}{2}} \right)\) 
• B.
  \(N\left( {\dfrac{1}{2};\dfrac{7}{2}} \right)\) 
• C.
  \(P\left( { – \dfrac{1}{2};\dfrac{7}{2}} \right)\) 
• D.
  \(M\left( { – \dfrac{1}{2}; – \dfrac{7}{2}} \right)\) 

Câu 29:

Biết \(\int\limits_0^1 {\sqrt {{x^2} + 4} .xdx}  = \dfrac{1}{a}\left( {\sqrt {{b^3}}  – c} \right)\). Tính \(Q = abc\). 

• A.
  \(Q = 120\) 
• B.
  \(Q = 15\) 
• C.
  \(Q =  – 120\) 
• D.
  \(Q = 40\) 

Câu 30:

Cho hai hàm số \(f\left( x \right)\) và \(g\left( x \right)\) liên tục trên \(K\) (với \(K\) là khoảng hoặc đoạn hoặc nửa khoảng của \(\mathbb{R}\)). Mệnh đề nào dưới đây sai? 

• A.
  \(\int {\left[ {f\left( x \right) – g\left( x \right)} \right]dx}  = \int {f\left( x \right)dx}  – \int {g\left( x \right)dx} \) 
• B.
  \(\int {f\left( x \right).g\left( x \right)dx}  = \int {f\left( x \right)dx} .\int {g\left( x \right)dx} \) 
• C.
  \(\int {kf\left( x \right)dx}  = k\int {f\left( x \right)dx} \)  với \(k\) là hằng số khác \(0\) 
• D.
  \(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx}  = \int {f\left( x \right)dx}  + \int {g\left( x \right)dx} \) 

Câu 31:

Tìm một căn bậc hai của \( – 5\). 

• A.
  \(i\sqrt 5 \) 
• B.
  \(i\sqrt { – 5} \) 
• C.
  \(\sqrt {5i} \) 
• D.
  \( – \sqrt {5i} \) 

Câu 32:

Cho hình phẳng D giới hạn bởi các đường \(y = x + 2,y = 0,x = 1\) và \(x = 3.\) Tính thể tích \(V\) của khối tròn xoay tạo thành khi quay hình D xung quanh trục \(Ox.\)

• A.
  \(V = \dfrac{{98}}{3}\) 
• B.
  \(V = 8\pi \)
• C.
  \(V = \dfrac{{98\pi }}{3}\)
• D.
  \(V = \dfrac{{98{\pi ^2}}}{3}\) 

Câu 33:

Gọi \({z_1}\) và \({z_2}\) là hai nghiệm phức của phương trình \({z^2} – 2z + 5 = 0\), trong đó \({z_2}\) có phần ảo âm. Tìm phần ảo \(b\) của số phức \(w = {\left[ {\left( {{z_1} – i} \right)\left( {{z_2} + 2i} \right)} \right]^{2018}}\). 

• A.
  \(b = {2^{1009}}\) 
• B.
  \(b = {2^{2017}}\) 
• C.
   \(b =  – {2^{2018}}\)
• D.
  \(b = {2^{2018}}\) 

Câu 34:

Trong không gian \(Oxyz,\) phương trình nào dưới đây là phương trình của mặt phẳng đi qua điểm \(M\left( {2;3; – 1} \right)\) và có véc tơ pháp tuyến \(\overrightarrow n  = \left( {2; – 2;5} \right)?\) 

• A.
  \(2x – 2y + 5z + 15 = 0\) 
• B.
  \(2x – 2y + 5z + 7 = 0\) 
• C.
  \(2x + 3y – z + 7 = 0\) 
• D.
  \(2x + 3y – z + 15 = 0\) 

Câu 35:

Biết \(\int {\left( {3{x^3} + 5{x^4}} \right)dx}  = A.{x^\alpha } + B.{x^\beta } + C\). Tính \(P = A.\alpha  + B.\beta \) 

• A.
  \(P = 37\) 
• B.
  \(P = 4\) 
• C.
  \(P = 29\) 
• D.
  \(P = 8\) 

Câu 36:

Trong không gian \(Oxyz,\) cho hai điểm \(A\left( {7; – 2;2} \right)\) và \(B\left( {1;2;4} \right)\). Phương trình nào dưới đây là  phương trình mặt cầu đường kính \(AB?\) 

• A.
  \({\left( {x – 4} \right)^2} + {y^2} + {\left( {z – 3} \right)^2} = 2\sqrt {14} \) 
• B.
  \({\left( {x – 4} \right)^2} + {y^2} + {\left( {z – 3} \right)^2} = 14\) 
• C.
  \({\left( {x – 4} \right)^2} + {y^2} + {\left( {z – 3} \right)^2} = 56\) 
• D.
  \({\left( {x – 7} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z – 2} \right)^2} = 14\) 

Câu 37:

Trong không gian Oxyz, cho điểm \(P\left( {3;1;3} \right)\) và đường thẳng \(d:\dfrac{{x – 3}}{1} = \dfrac{{y + 4}}{3} = \dfrac{{z – 2}}{3}\). Phương trình nào dưới đây là phương trình của mặt phẳng đi qua điểm \(P\) và vuông góc với đường thẳng \(d\)? 

• A.
  \(x – 4y + 3z + 3 = 0\) 
• B.
  \(x + 3y + 3z – 3 = 0\)

   

• C.
  \(3x + y + 3z – 15 = 0\) 
• D.
  \(x + 3y + 3z – 15 = 0\) 

Câu 38:

Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):5x + 3y – 2z + 1 = 0\). Tìm tọa độ một véc tơ pháp tuyến của mặt phẳng \(\left( P \right).\) 

• A.
  \(\overrightarrow u  = \left( {5;3; – 2} \right)\) 
• B.
  \(\overrightarrow n  = \left( {5;3;2} \right)\) 
• C.
  \(\overrightarrow p  = \left( {5; – 3; – 2} \right)\) 
• D.
  \(\overrightarrow q  = \left( { – 5; – 3;1} \right)\) 

Câu 39:

Trong không gian Oxyz, cho hai điểm \(A\left( {5;0;4} \right)\) và \(B\left( {3;4;2} \right)\). Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng \(AB\)? 

• A.
  \(4x + 2y + 3z – 11 = 0\) 
• B.
  \(x – 2y + z – 11 = 0\) 
• C.
  \(4x + 2y + 3z – 3 = 0\) 
• D.
  \(x – 2y + z – 3 = 0\) 

Câu 40:

Trong không gian \(Oxyz,\) cho ba điểm \(A\left( {2;0;0} \right),B\left( {0;0;3} \right)\) và \(C\left( {0;5;0} \right).\) Phương trình nào dưới đây là phương trình của mặt phẳng \(\left( {ABC} \right)?\) 

• A.
  \(\dfrac{x}{2} + \dfrac{y}{5} + \dfrac{z}{3} =  – 1\) 
• B.
  \(\dfrac{x}{2} + \dfrac{y}{5} + \dfrac{z}{3} = 1\) 
• C.
  \(\dfrac{x}{2} + \dfrac{y}{3} + \dfrac{z}{5} = 1\) 
• D.
  \(\dfrac{x}{2} + \dfrac{y}{3} + \dfrac{z}{5} = 0\)