GIẢI CHI TIẾT Giải SBT Bài CUỐI Chương 3 – SBT Toán 7 TẬP 1 – Cánh diều
================
Giải bài 16 trang 94 SBT Toán 7 Cánh diều tập 1 – CD
Trong các phát biểu sau, phát biểu nào đúng?
A. Hình lăng trụ đứng tứ giác có 6 mặt, 8 đỉnh, 8 cạnh.
B. Hình lăng trụ đứng tứ giác có 4 mặt, 6 đỉnh, 8 cạnh.
C. Hình lăng trụ đứng tứ giác có 4 mặt, 8 đỉnh, 12 cạnh.
D. Hình lăng trụ đứng tứ giác có 6 mặt, 8 đỉnh, 12 cạnh.
Phương pháp giải:
Ta xem hình lăng trụ đứng tứ giác để biết hình lăng trụ đứng có mấy mặt, mấy đỉnh, mấy cạnh và nhận xét phát biểu đúng hay sai.
Lời giải chi tiết:
Đáp án: D. Hình lăng trụ đứng tứ giác có 6 mặt, 8 đỉnh, 12 cạnh.
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
Giải bài 17 trang 94 SBT Toán 7 Cánh diều tập 1 – CD
Một hình lập phương có thể tích là \(125{\rm{ }}{{\rm{m}}^3}\). Diện tích xung quanh của hình lập phương đó là:
A. \(125{\rm{ }}{{\rm{m}}^2}\).
B. \({\rm{500 }}{{\rm{m}}^2}\).
C. \(150{\rm{ }}{{\rm{m}}^2}\).
D. \(100{\rm{ }}{{\rm{m}}^2}\).
Phương pháp giải:
Muốn tính diện tích xung quanh của hình lập phương ta cần biết độ dài cạnh của hình lập phương.
Bước 1: Tính cạnh của hình lập phương
Bước 2: Diện tích xung quanh hình lập phương cạnh a là: \(S_{xq}=4.a.a\)
Lời giải chi tiết:
Thể tích của hình lập phương là \(125{\rm{ }}{{\rm{m}}^3}\), suy ra cạnh của hình lập phương \(\sqrt[3]{{125}} = 5{\rm{ m}}\).
Vậy diện tích xung quanh của hình lập phương đó là:
\(4.5{\rm{ }}{\rm{. 5 }}{\rm{ = 100 (}}{{\rm{m}}^2})\).
Đáp án: D. \(100{\rm{ }}{{\rm{m}}^2}\).
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
Giải bài 18 trang 94 SBT Toán 7 Cánh diều tập 1 – CD
Một bể rỗng không chứa nước có dạng hình hộp chữ nhật với chiều dài là 2,4 m, chiều rộng là 1,5 m. chiều cao là 1 m. Người ta sử dụng một máy bơm nước có công suất 30l/phút để bơm đầy bể đó. Số giờ để bể đó đầy nước là:
A. \(\dfrac{{13}}{3}\) giờ. B. 120 giờ. C. 2 giờ. D. \(\dfrac{{49}}{{18}}\) giờ.
Phương pháp giải:
Muốn tính số giờ đầy bể, ta cần biết dung tích hay thể tích của bể là bao nhiêu.
Thể tích hình hộp chữ nhật kích thước a,b,c là: \(V =a.b.c\)
Lời giải chi tiết:
Thể tích của bể có dạng hình hộp chữ nhật là:
\(2,4{\rm{ }}{\rm{. 1,5 }}{\rm{. 1 = 3,6 (}}{{\rm{m}}^3}) = 3600{\rm{ (d}}{{\rm{m}}^3}) = 3600l\).
Vậy thời gian để bể đầy nước là:
\(3600:30 = 120\) (phút) = 2 giờ.
Đáp án: C. 2 giờ.
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
Giải bài 19 trang 94 SBT Toán 7 Cánh diều tập 1 – CD
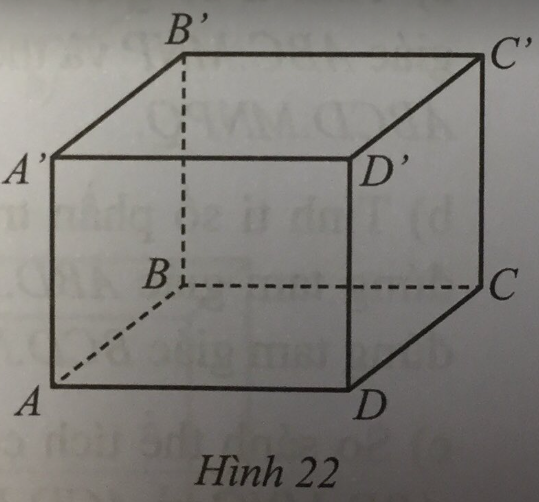
Cho hình hộp chữ nhật ABCD.A’B’C’D’ với các kích thước \(AB = 20{\rm{ cm}}\), \(BC = 15{\rm{ cm}}\), \(CC’ = 12{\rm{ cm}}\) (Hình 22). Tính tỉ số diện tích xung quanh và tổng diện tích hai đáy của hình hộp chữ nhật đó là:

A. \(\dfrac{5}{{14}}\) B. \(\dfrac{7}{5}\).
C. \(\dfrac{5}{7}\). D. \(\dfrac{{14}}{5}\).
Phương pháp giải:
Muốn tính tỉ số diện tích xung quanh và tổng diện tích hai đáy của hình hộp chữ nhật đó, ta cần tính diện tích xung quanh và tổng diện tích hai đáy của hình đó.
Lời giải chi tiết:
Diện tích xung quanh của hình hộp chữ nhật là:
\(2.(20+15).12 = 840 (cm^2)\).
Tổng diện tích hai đáy của hình hộp chữ nhật là:
\(20{\rm{ }}{\rm{. 15 }}{\rm{. 2 = 600 (c}}{{\rm{m}}^2})\).
Vậy tỉ số diện tích xung quanh và tổng diện tích hai đáy của hình hộp chữ nhật đó là:
\(\dfrac{{840}}{{600}} = \dfrac{7}{5}\).
Đáp án: B. \(\dfrac{7}{5}\).
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
Giải bài 20 trang 94 SBT Toán 7 Cánh diều tập 1 – CD
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Diện tích xung quanh của hình hộp chữ nhật bằng một nửa tổng diện tích các mặt.
b) Thể tích của hình hộp chữ nhật bằng tích chiều dài nhân với chiều rộng rồi nhân với chiều cao.
c) Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 6.
d) Thể tích của hình lập phương bằng diện tích của cạnh nhân cạnh rồi nhân với cạnh.
Phương pháp giải:
Ta xét từng phát biểu để xét tính đúng – sai.
Lưu ý phân biệt giữa diện tích xung quanh và diện tích toàn phần của hình.
Lời giải chi tiết:
Phát biểu a) sai: Diện tích xung quanh của hình hộp chữ nhật bằng tổng diện tích các mặt trừ đi tổng diện tích hai đáy.
Phát biểu b) đúng: Thể tích của hình hộp chữ nhật bằng tích chiều dài nhân với chiều rộng rồi nhân với chiều cao.
Phát biểu c) sai: Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 4.
Phát biểu d) đúng: Thể tích của hình lập phương bằng diện tích của cạnh nhân cạnh rồi nhân với cạnh.
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
Giải bài 21 trang 94 SBT Toán 7 Cánh diều tập 1 – CD
a) Một hình lập phương có thể tích là \(216{\rm{ d}}{{\rm{m}}^3}\). Tính diện tích xung quanh của hình lập phương đó.
b) Hình hộp chữ nhật thứ nhất có các kích thước: chiều dài, chiều rộng, chiều cao lần lượt bằng a (m), b (m), c (m), Hình hộp chữ nhật thứ hai có các kích thước: chiều dài, chiều rộng, chiều cao lần lượt bằng 3a (m), 2b (m), 4c (m). Tính tỉ số giữa thể tích của hình hộp chữ nhật thứ hai và thể tích của hình hộp chữ nhật thứ nhất.
Phương pháp giải:
a) Muốn tính diện tích xung quanh của hình lập phương, ta cần tính độ dài cạnh của hình lập phương đó.
b) Muốn tính tỉ số giữa thể tích hình hộp chữ nhật thứ hai và thể tích hình hộp chữ nhật thứ nhất, ta cần tính thể tích của hai hình hộp chữ nhật.
Lời giải chi tiết:
a) Thể tích của hình lập phương là \({\rm{216 d}}{{\rm{m}}^3}\), suy ra cạnh của hình lập phương \(\sqrt[3]{{216}} = 6{\rm{ dm}}\).
Vậy diện tích xung quanh của hình lập phương đó là:
\({\rm{6 }}{\rm{. 6 }}{\rm{. 4 = 144 (d}}{{\rm{m}}^2})\).
b) Thể tích của hình hộp chữ nhật thứ hai là:
\(3a{\rm{ }}.{\rm{ }}2b{\rm{ }}.{\rm{ }}4c = 24abc{\rm{ (}}{{\rm{m}}^3})\).
Thể tích của hình hộp chữ nhật thứ nhất là:
\(a{\rm{ }}.{\rm{ }}b{\rm{ }}.{\rm{ }}c = abc{\rm{ (}}{{\rm{m}}^3})\).
Vậy tỉ số giữa thể tích của hình hộp chữ nhật thứ hai và thể tích của hình hộp chữ nhật thứ nhất là:
\(\dfrac{{24abc}}{{abc}} = 24\).
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
Giải bài 22 trang 95 SBT Toán 7 Cánh diều tập 1 – CD
Một hình lăng trụ đứng tứ giác có chu vi đáy là 12 dm. Nếu tăng chiều cao thêm 2 dm và giảm chu vi đáy đi 4 dm thì diện tích xung quanh của hình lăng trụ đứng đã cho giảm \(2{\rm{0 d}}{{\rm{m}}^2}\). Tính diện tích xung quanh của hình lăng trụ đứng ban đầu.
Phương pháp giải:
Muốn tính diện tích xung quanh của hình lăng trụ đứng ban đầu, ta cần tính độ dài cạnh bên của hình lăng trụ đó.
Lời giải chi tiết:
Gọi độ dài cạnh bên của hình lăng trụ đứng tứ giác ban đầu là x (dm) (x > 0).
Khi đó, diện tích xung quanh của hình lăng trụ ban đầu là: \(12x{\rm{ (d}}{{\rm{m}}^2})\).
Diện tích xung quanh của hình lăng trụ sau khi tăng chiều cao thêm 2 dm và giảm chu vi đáy đi 4 dm là:
\((12 – 4).(x – 2) = 8x + 16{\rm{ (d}}{{\rm{m}}^2})\).
Mà khi tăng chiều cao thêm 2 dm và giảm chu vi đáy đi 4 dm thì diện tích xung quanh của hình lăng trụ đứng đã cho giảm \(2{\rm{0 d}}{{\rm{m}}^2}\) nên suy ra:
\(\begin{array}{l}8x + 16 = 12x – 20\\ \Rightarrow 20 + 16 = 12x – 8x\\ \Rightarrow 36 = 4x\\ \Rightarrow x = 9\end{array}\)
Suy ra cạnh bên của hình lăng trụ đứng tứ giác là 9 dm.
Vậy diện tích xung quanh của hình lăng trụ ban đầu là:
\(12{\rm{ }}{\rm{. 9 = 108 (d}}{{\rm{m}}^2})\).
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
Giải bài 23 trang 95 SBT Toán 7 Cánh diều tập 1 – CD
a) Một hình lăng trụ đứng tam giác có độ dài cạnh bên bằng 16 cm và đáy là tam giác với độ dài các cạnh lần lượt là 4 cm, 8 cm, 11 cm. Tính diện tích xung quanh của hình lăng trụ đó.
b) Một hình lăng trụ đứng tứ giác có đáy là hình thoi với độ dài cạnh đáy bằng 17 cm. Tính chiều cao của hình lăng trụ đó, biết các đường chéo của đáy lần lượt bằng 16 cm, 30 cm và diện tích toàn phần của hình lăng trụ (tức tổng diện tích các mặt) bằng 1 840 \({\rm{c}}{{\rm{m}}^2}\).
c) Một hình lăng trụ đứng tứ giác có độ dài cạnh bên là 12 cm và đáy là hình thang với độ dài đáy bé, đáy lớn, đường cao lần lượt là 15 cm, 17 cm, 13 cm. Tính thể tích của hình lăng trụ đó.
Phương pháp giải:
a) Diện tích xung quanh của hình lăng trụ bằng chu vi đáy nhân với cạnh bên.
b) Muốn tính chiều cao của hình lăng trụ, ta cần tính diện tích xung quanh của hình lăng trụ đó.
c) Thể tích của hình lăng trụ tứ giác bằng diện tích đáy nhân cạnh bên.
Lời giải chi tiết:
a) Diện tích xung quanh của hình lăng trụ đứng tam giác đó là:
\((4 + 8 + 11){\rm{ }}.{\rm{ }}16 = 368{\rm{ (c}}{{\rm{m}}^2})\).
b) Diện tích hai mặt đáy của hình lăng trụ đứng tứ giác là:
\(2{\rm{ }}.{\rm{ }}\dfrac{{16{\rm{ }}.{\rm{ }}30}}{2} = 480{\rm{ (c}}{{\rm{m}}^2})\).
Diện tích xung quanh của hình lăng trụ đứng tứ giác đó là:
\(1{\rm{ }}840 – 480 = 1{\rm{ }}360{\rm{ (c}}{{\rm{m}}^2})\).
Chiều cao của hình lăng trụ đứng tứ giác đó là:
\(1{\rm{ 360 : (4 }}{\rm{. 17) = 20 (cm)}}\).
c) Thể tích của hình lăng trụ tứ giác đó là:
\(\dfrac{{(15 + 17){\rm{ }}.{\rm{ }}13}}{2}{\rm{ }}.{\rm{ }}12 = 2{\rm{ }}496{\rm{ (c}}{{\rm{m}}^3})\).
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
Giải bài 24 trang 95 SBT Toán 7 Cánh diều tập 1 – CD
Hình 23 minh họa các mặt của một hình được ghép bởi nhiều khối lập phương nhỏ cạnh 1 cm.
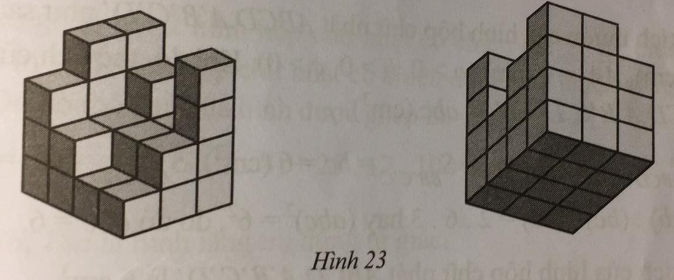
a) Hình được ghép có bao nhiêu khối lập phương nhỏ cạnh 1 cm?
b) Tính thể tích của hình được ghép.
c) Người ta sơn màu lên bề ngoài của hình được ghép. Có bao nhiêu khối lập phương nhỏ cạnh 1 cm không được sơn mặt nào?
Phương pháp giải:
a) Muốn biết hình được ghép từ bao nhiêu khối lập phương, ta tính theo các lớp cấu thành nên hình đó.
b) Mỗi khối lập phương nhỏ có thể tích là \(1{\rm{ c}}{{\rm{m}}^3}\) nên thể tích của các hình được ghép bằng số khối lập phương nhân với thể tích mỗi khối lập phương nhỏ.
c) Quan sát hình được ghép và các mặt của các khối lập phương nhỏ.
Lời giải chi tiết:
a) Hình được ghép từ 4 lớp tính từ dưới lên:
Lớp dưới cùng (lớp thứ nhất) có: \(4{\rm{ }}{\rm{. 3 = 12}}\) khối lập phương nhỏ cạnh 1 cm;
Lớp thứ hai có: \(12 – 2 = 10\) khối lập phương nhỏ cạnh 1 cm;
Lớp thứ ba có 5 khối lập phương nhỏ cạnh 1 cm;
Lớp trên cúng (lớp thứ tư) có 3 khối lập phương nhỏ cạnh 1 cm.
Vậy hình được ghép bởi: \(12 + 10 + 5 + 3 = 30\) khối lập phương nhỏ cạnh 1 cm.
b) Thể tích của hình được ghép bằng số khối lập phương nhân với thể tích mỗi khối lập phương.
Mà thể tích mỗi khối lập phương cạnh 1 cm là \(1{\rm{ c}}{{\rm{m}}^3}\) nên thể tích của hình được ghép là:
\(30{\rm{ }}{\rm{. 1 = 30 (c}}{{\rm{m}}^3})\).
c) Do sơn màu lên bề ngoài của hình được ghép nên khối lập phương nhỏ nào cũng có mặt được sơn.
Vậy số khối lập phương nhỏ cạnh 1 cm không được sơn mặt nào là: 0.
Giải bài tập Toán 7 Cánh diều Bài tập cuối chương 3
=============
