Giải bài 10.1 trang 63 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
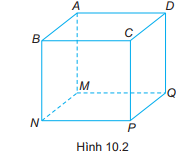
Gọi tên các đỉnh, cạnh, đường chéo, mặt của hình lập phương trong Hình 10.2.

Phương pháp giải:
Hình lập phương có 6 đỉnh, 12 cạnh, 4 đường chéo, 6 mặt.
Lời giải chi tiết:
-Các đỉnh: A, B, C, D, A’, B’, C’, D’
-Cạnh: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’; AA’; BB’; CC’; DD’.
-Các đường chéo: AC’; BD’; CA’; DB’.
-Các mặt: ABCD, A’B’C’D’, ABB’A’, BCC’B’, CDD’C’, ADD’A’.
–>
— *****
Giải bài 10.2 trang 63 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Hộp đựng khối rubik có dạng một hình lập phương có cạnh 3cm, được làm bằng bìa cứng. Tính thể tích của chiếc hộp và diện tích bìa cứng để làm chiếc hộp đó.
Phương pháp giải:
-Thể tích hình lập phương có cạnh a là: V = a3
-Diện tích bìa cứng = diện tích toàn phần = 6 . Diện tích 1 mặt = 6 . a2
Lời giải chi tiết:
Thể tích của chiếc hộp là:
V = a3 = 33 = 27 (cm3)
Diện tích bìa cứng dùng để làm chiếc hộp là:
S = 6.32 = 54 (cm2)
–>
— *****
Giải bài 10.3 trang 63 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Một cái bể chứa nước có dạng hình hộp chữ nhật dài 2 m, rộng 1,5 m, cao 1,2 m. Lúc đầu bể chứa đầy nước, sau đó người ta lấy ra 45 thùng nước, mỗi thùng 20 lít. Hỏi sau khi lấy nước ra, mực nước trong bể cao bao nhiêu?
Phương pháp giải:
-Tính thể tích hình hộp chữ nhật
-Tính lượng nước lấy ra
-Tính lượng nước còn lại trong bể
-V = Sđáy . chiều cao \( \Rightarrow h = \dfrac{V}{{{S_{day}}}}\)
Lời giải chi tiết:
Thể tích của bể chứa (hình hộp chữ nhật) là:
\(V = 2 \cdot 1,5 \cdot 1,2 = 3,6\left( {{m^3}} \right)\)
Đổi \(3,6{m^3} = 3\,600d{m^3} = 3\,600\,l\)
Lượng nước lấy ra là: 20 . 45 = 900 (l)
Lượng nước còn lại trong bể là: 3 600 – 900 = 2 700 (l)
Đổi 2 700 l = 2,7 m3.
Diện tích đáy bể là: 2 . 1,5 = 3 (m2)
Mực nước trong bể cao là: 2,7 : 3 = 0,9 (m)
–>
— *****
Giải bài 10.4 trang 63 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Tính thể tích của một hình lập phương, biết tổng diện tích các mặt của nó là 216 cm2.
Phương pháp giải:
Tính diện tích 1 mặt từ đó suy ra cạnh của hình lập phương.
Lời giải chi tiết:
Hình lập phương có 6 mặt bằng nhau
Diện tích một mặt của hình lập phương là: 216 : 6 = 36 (cm2)
Gọi độ dài cạnh hình lập phương là a. Ta có: \({a^2} = 36 \Rightarrow a = 6\)
Thể tích hình lập phương là: \(V = {a^3} = {6^3} = 216\left( {c{m^3}} \right)\)
–>
— *****
Giải bài 10.5 trang 63 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Một bể nước dạng hình hộp chữ nhật có chiều dài 2m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước trong bể cao 0,8 m.
a)Tính chiều rộng của bể nước.
b)Người ta đổ thêm vào bể 60 thùng nước nữa thì đầy bể. Hỏi bể nước cao bao nhiêu mét?
Phương pháp giải:
a)
-Tính thể tích nước đổ vào bể
-\(V = a.b.h \Rightarrow b = \dfrac{V}{{a.h}}\)
b)
– Tính lượng nước khi đầy bể (thể tích của bể).
-\(V = a.b.h \Rightarrow h = \dfrac{V}{{a.b}}\)
Lời giải chi tiết:
a)
Thể tích nước đổ vào bể là: V = 120 . 20 = 2 400 (l).
Đổi 2 400 (l) = 2 400 dm3 = 2,4 (m3)
Ta có: \(V = a.b.h \Rightarrow b = \dfrac{V}{{a.h}}\)
Chiều rộng của bể là: \(b = \dfrac{{2,4}}{{2 \cdot 0,8}} = 1,5\left( m \right)\).
b)
Tổng số thùng nước để đầy bể là: 120 + 60 = 180 (thùng nước)
Lượng nước khi đầy bể (thể tích của bể) là: 180 . 20 = 3 600 (l)
Đổi 3 600 l = 3,6 (m3)
Ta có: \(V = a.b.h \Rightarrow h = \dfrac{V}{{a.b}}\)
Chiều cao của bể là:\(h = \dfrac{{3,6}}{{2.1,5}} = 1,2\left( m \right)\)
–>
— *****
Giải bài 10.6 trang 63 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
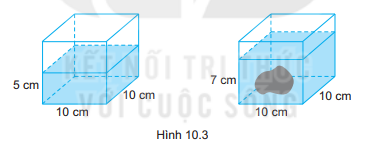
Bạn Hà có một bể cá có dạng hình lập phương có độ dài cạnh 10 cm. Ban đầu nước trong bể có độ cao 5 cm. Bạn Hà bỏ thêm vào trong bể một hòn đá trang trí chìm trong nước thì nước trong bể có độ cao 7cm (H.10.3). Hỏi hòn đá bạn Hà bỏ vào bể có thể tích bao nhiêu cm3 ?
Phương pháp giải:
-Tính tổng thể tích của nước và hòn đá.
-Tính thể tích nước trong bể ban đầu.
Lời giải chi tiết:
Tổng thể tích của nước và hòn đá là:
\({V_1} = 10 \cdot 10 \cdot 7 = 700\left( {c{m^3}} \right)\)
Thể tích nước trong bể ban đầu là:
\({V_2} = 10 \cdot 10 \cdot 5 = 500\left( {c{m^3}} \right)\)
Thể tích hòn đá là:
\(V = {V_1} – {V_2} = 700 – 500 = 200\left( {c{m^3}} \right)\)
–>
— *****
Giải bài 10.7 trang 63 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Một bể nước hình hộp chữ nhật có kích thước đáy là 2 m x 3 m chưa có nước. Mở vòi nước chảy vào bể trong 8 giờ, mỗi giờ vòi chảy được 500 lít nước. Hỏi khi đó mực nước trong bể cao bao nhiêu mét?
Phương pháp giải:
-Tính lượng nước vòi chảy vào bể trong 8 giờ.
-Áp dụng công thức: \(V = a.b.h \Rightarrow h = \dfrac{V}{{a.b}}\)
Lời giải chi tiết:
Đổi 500 lít = 500 dm3 = 0,5 m3
Lượng nước vòi chảy vào bể trong 8 giờ là: 0,5 . 8 = 4 (m3)
Gọi h là chiều cao nước trong bể, ta có: \(2.3.h = 4 \Rightarrow h = \dfrac{4}{{2.3}} = \dfrac{2}{3}\left( m \right)\)
Vậy mực nước trong bể cao \(\dfrac{2}{3}m\)
–>
— *****
Giải bài 10.8 trang 63 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Tính thể tích của hình hộp chữ nhật biết nó có diện tích xung quanh là 10 000 cm2, chiều cao bằng 50 cm và chiều dài hơn chiều rộng 12 cm.
Phương pháp giải:
-\({S_{xq}} = {C_{{\rm{d}}ay}}.h \Rightarrow {C_{day}} = \dfrac{{{S_{xq}}}}{h}\)
-Tính tổng chiều dài và rộng (nửa chu vi đáy)
-Tính chiều dài, chiều rộng
Số lớn = (tổng + hiệu ) : 2
Số bé = (tổng – hiệu) : 2
Lời giải chi tiết:
Chu vi đáy của hình hộp chữ nhật là:
\({S_{xq}} = {C_{{\rm{d}}ay}}.h \Rightarrow {C_{day}} = \dfrac{{{S_{xq}}}}{h} = \dfrac{{10\,000}}{{50}} = 200\left( {cm} \right)\)
Nửa chu vi đáy của hình hộp chữ nhật là: 200 : 2 = 100 (cm)
Chiều dài của hình hộp chữ nhật là: (100 + 12) : 2 = 56 (cm)
Chiều rộng của hình hộp chữ nhật là: 100 – 56 = 44 (cm)
Thể tích của hình hộp chữ nhật là: V = a.b.h = 56 . 44. 50 = 123 200 (cm3)
–>
— *****
