Giải Câu hỏi 1 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Hình hộp chữ nhật có bao nhiêu mặt?
A.5
B.6
C.7
D.8
Phương pháp giải:
Hình hộp chữ nhật có 6 mặt
Lời giải chi tiết:
Chọn B
–>
— *****
Giải Câu hỏi 2 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Hình lập phương có bao nhiêu đỉnh?
A.2
B.4
C.6
D.8
Phương pháp giải:
Hình lập phương có 8 đỉnh
Lời giải chi tiết:
Chọn D
–>
— *****
Giải Câu hỏi 3 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Hình hộp chữ nhật có bao nhiêu cạnh?
A.4
B.12
C.10
D.8
Phương pháp giải:
Hình hộp chữ nhật có 12 cạnh
Lời giải chi tiết:
Chọn B
–>
— *****
Giải Câu hỏi 4 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Hình lập phương có bao nhiêu đường chéo?
A.2
B.3
C.4
D.5
Phương pháp giải:
Hình lập phương có 4 đường chéo.
Lời giải chi tiết:
Chọn C
–>
— *****
Giải Câu hỏi 5 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Mặt bên của hình lăng trụ đứng tam giác là:
A.Hình tam giác
B.Hình thoi
C.Hình chữ nhật
D.Hình lục giác đều
Phương pháp giải:
Mặt bên của hình lăng trụ đứng tam giác là hình chữ nhật.
Lời giải chi tiết:
Chọn C
–>
— *****
Giải Câu hỏi 6 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Các cạnh bên của hình lăng trụ đứng:
A.Song song và không bằng nhau
B.Cắt nhau
C.Vuông góc với nhau
D.Song song và bằng nhau
Phương pháp giải:
Các cạnh bên của hình lăng trụ đứng: Song song và bằng nhau
Lời giải chi tiết:
Chọn D
–>
— *****
Giải Câu hỏi 7 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Thể tích hình lập phương có cạnh dài 5 cm là:
A.25 cm3
B. 125 cm2
C. 125 cm3
D. 20 cm2
Phương pháp giải:
Thể tích hình lập phương cạnh a(cm) là: \(a.a.a (cm^3)\)
Lời giải chi tiết:
Thể tích hình lập phương là: 5 . 5 . 5 = 125 cm3.
Chọn C
–>
— *****
Giải Câu hỏi 8 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Hình lăng trụ đứng tam giác có đáy là tam giác đều cạnh 3 cm, chiều cao hình lăng trụ bằng 10 cm. Diện tích xung quanh của hình lăng trụ đó là:
A.30 cm2
B.90 cm2
C. 90 cm3
D. 13 cm2
Phương pháp giải:
Diện tích xung quanh lăng trụ = chu vi đáy . chiều cao
Lời giải chi tiết:
Diện tích xung quanh của hình lăng trụ đó là: \({S_{xq}} = {C_{day}} \cdot h = \left( {3 + 3 + 3} \right).10 = 9 \cdot 10 = 90\left( {c{m^2}} \right)\).
Chọn C
–>
— *****
Giải Câu hỏi 9 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Một hình lăng trụ đứng, đáy là hình thang, chiều cao hình lăng trụ bằng 5 cm. Thể tích của hình lăng trụ nói trên bằng 50 cm3. Diện tích một đáy lăng trụ bằng:
A.10 cm2
B.250 cm2
C.55 cm2
D.10 cm3
Phương pháp giải:
Diện tích đáy lăng trụ = Thể tích lăng trụ : chiều cao
Lời giải chi tiết:
Diện tích đáy hình lăng trụ là:
\(V = {S_{day}} \cdot h \Rightarrow {S_{day}} = \frac{V}{h} = \frac{{50}}{5} = 10\left( {c{m^2}} \right)\)
Chọn A
–>
— *****
Giải Câu hỏi 10 trang 67 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Một hình hộp chữ nhật có đáy là hình vuông có thể tích 150 cm3. Chiều cao của hình hộp bằng 6 cm. Chu vi đáy của hình hộp chữ nhật là:
A.25 cm
B.20 cm2
C. 20 cm
D. 900 cm
Phương pháp giải:
Bước 1: Tính cạnh đáy của hình hộp chữ nhật
Bước 2: Tính chu vi đáy của hình hộp
Lời giải chi tiết:
Gọi chiều dài đáy là a, chiều rộng đáy là b.
Mà đáy là hình vuông nên a = b
Ta có: \(V = {S_{day}} \cdot h \Rightarrow {S_{day}} = \frac{{150}}{6} = 25 \Rightarrow ab = 25 \Rightarrow {a^2} = 25 \Rightarrow a = 5\)
Vậy chu vi đáy của hình hộp chữ nhật là: 4.5 = 20 (cm).
–>
— *****
Giải bài 10.16 trang 68 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
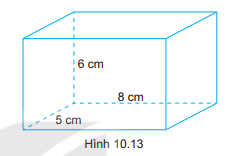
Cho hình hộp chữ nhật có kích thước như Hình 10.13. Tính thể tích, diện tích xung quanh của hình hộp chữ nhật.

Phương pháp giải:
-Thể tích: \(V = a.b.h\)
-Diện tích xung quanh: \({S_{day}} = {C_{day}}.h\)
Lời giải chi tiết:
Thể tích hình hộp chữ nhật là: \(V = a.b.h = 8.5.6 = 240\left( {c{m^3}} \right)\)
Chu vi đáy hình hộp chữ nhật là: \(C = 2.\left( {a + b} \right) = 2.\left( {8 + 5} \right) = 13.2 = 26\left( {cm} \right)\)
Diện tích xung quanh của hình hộp chữ nhật là: \(S = {C_{day}}.h = 26.6 = 156\left( {c{m^2}} \right)\).
–>
— *****
Giải bài 10.17 trang 68 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Một thùng đựng hàng có nắp dạng hình hộp chữ nhật có chiều dài 3m, chiều rộng 2m và chiều cao 1,8m. Người thợ cần bao nhiêu kilogam sơn để đủ sơn toàn bộ mặt ngoài của chiếc thùng đó, biết rằng mỗi kilogam sơn có thể sơn được 5 m2 mặt thùng.
Phương pháp giải:
Diện tích sơn cần dùng chính là tính diện tích toàn phần của thùng hàng.
\(S_{tp} = S_{xq} + S _{2đáy}\)
Lời giải chi tiết:
Diện tích xung quanh của thùng đựng hàng đó là:
\({S_{xq}} = {C_{đáy}}.h = 2.\left( {a + b} \right).h = \left( {3 + 2} \right).2.1,8 = 18\left( {{m^2}} \right)\)
Diện tích hai đáy của thùng đựng hàng là:
\({S_{2đáy}} = 2.a.b = 2.3.2 = 12\left( {{m^2}} \right)\)
Diện tích toàn phần của thùng đựng hàng đó là:
\({S_{xq}} = {S_{xq}} + 2{S_{đáy}} = 18 + 12 = 30\left( {{m^2}} \right)\)
Số kilogam sơn cần dùng là: 30 : 5 = 6 (kg)
–>
— *****
Giải bài 10.18 trang 68 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75 m. Hỏi người thợ phải dùng bao nhiêu viên gạch men hình chữ nhật để lát đáy và xung quanh thành bể đó? Biết rằng diện tích mạch vữa lát không đáng kể và mỗi viên gạch có chiều dài 25 cm, chiều rộng 20 cm.
Phương pháp giải:
-Diện tích cần lát gạch = diện tích xung quanh + diện tích đáy bể.
-Diện tích 1 viên gạch.
Lời giải chi tiết:
Diện tích xung quanh của bể là:
\({S_{xq}} = {C_{day}}.h = 2\left( {a + b} \right).h = 2.\left( {12 + 5} \right).2,75 = 93,5\left( {{m^2}} \right)\)
Diện tích đáy bể (hình chữ nhật) là:
\({S_{day}} = a.b = 12.5 = 60\left( {{m^2}} \right)\)
Diện tích cần lát gạch là:
\(S = {S_{xq}} + {S_{day}} = 93,5 + 60 = 153,5\left( {c{m^2}} \right)\)
Diện tích một viên gạch men là:
\({S_{viengach}} = 20.25 = 500\left( {c{m^2}} \right)\)
Đổi \(500c{m^2} = 0,05{m^2}\)
Số viên gạch men cần dùng là: \(153,5:0,05 = 3\,070\) (viên)
–>
— *****
Giải bài 10.19 trang 68 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Thiết bị máy được xếp vào các hình lập phương có diện tích toàn phần bằng 96 dm2. Người ta xếp các hộp đó vào trong một thùng hình lập phương làm bằng tôn không có nắp. Khi gò một thùng như thế hết 3,2 m2 tôn (diện tích các mép hàn không đáng kể). Hỏi mỗi thùng đựng được bao nhiêu hộp thiết bị nói trên?
Phương pháp giải:
-Tính thể tích của một hộp đựng thiết bị: Tính độ dài cạnh (Hình lập phương có 6 cạnh)
-Tính thể tích thùng đựng hàng: Tính độ dài cạnh (Thùng đựng hàng có 5 mặt)
-Tính số hộp thiết bị đựng trong một thùng: Lấy thể tích thùng đựng hàng : thể tích của 1 hộp đựng thiết bị.
Lời giải chi tiết:
Đổi \(3,2{m^2} = 320d{m^2}\)
Diện tích một mặt của hộp thiết bị là: \(96:6 = 16\left( {d{m^2}} \right)\) (hình lập phương có 6 mặt)
Cạnh của hộp thiết bị là: \(4\) (vì \(4.4 = 16\))
Thể tích của một hộp đựng thiết bị là: \({4^3} = 64\left( {d{m^3}} \right)\)
Diện tích một mặt của thùng đựng hàng là: \(320:5 = 64\left( {d{m^2}} \right)\) (thùng lập phương k có lắp nên có 5 mặt)
Cạnh của thùng đựng hàng là: 8 (vì \({8^2} = 64\))
Thể tích thùng đựng hàng là: \({8^3} = 512\left( {d{m^3}} \right)\)
Số hộp thiết bị đựng trong một thùng là: \(512:64 = 8\) (hộp).
–>
— *****
Giải bài 10.20 trang 68 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
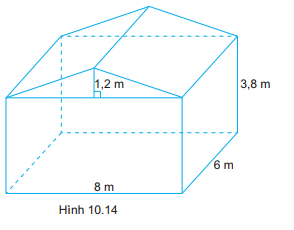
Một nhà kính trồng hoa có hình dạng và kích thước như Hình 10.14. Nhà kính có hình dạng gồm một hình lăng trụ đứng tam giác và một hình hộp chữ nhật. Tính thể tích của nhà kính.
Phương pháp giải:
Thể tích nhà kính = thể tích hình lăng trụ tam giác + thể tích hình hộp chữ nhật.
Lời giải chi tiết:
Thể tích hình lăng trụ đứng tam giác là: \({V_1} = {S_1}.h = \left( {\frac{1}{2} \cdot 1,2 \cdot 8} \right) \cdot 6 = 28,8\left( {{m^3}} \right)\)
Thể tích hình hộp chữ nhật là: \({V_2} = {S_2}.h = \left( {8 \cdot 6} \right) \cdot 3,8 = 182,4\left( {{m^3}} \right)\)
Thể tích của nhà kính là: \(V = {V_1} + {V_2} = 28,8 + 182,4 = 211,2\left( {{m^3}} \right)\)
–>
— *****
