Giải bài 3.10 trang 39 SBT Toán 10 – KN

Giải bài 3.10 trang 39 SBT Toán 10 – KN – KẾT NỐI TRI THỨC
CỦA BÀI HỌC: Bài 6. Hệ thức lượng trong tam giác – SBT Toán 10 KNTT

=======

Đề bài

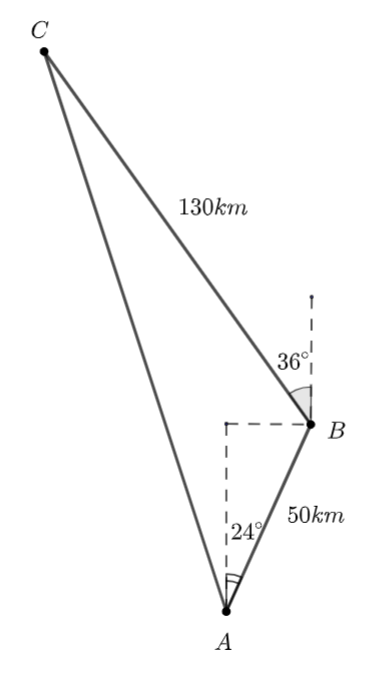
Một tàu các xuất phát từ đảo \(A,\) chạy 50 km theo hướng \(N{24^ \circ }E\) đến đảo \(B\) để lấy thêm ngư cụ, rồi chuyển hướng \(N{36^ \circ }W\) chạy tiếp 130 km đến ngư trường \(C.\)

a) Tính khoảng cách từ vị trí xuất phát từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị đo ki lô mét).

b) Tìm hướng từ A đến C ( đơn vị đến hàng đơn vị, theo đơn vị độ).

Phương pháp giải

– Tính \(\widehat B\)

– Áp dụng định lý cosin để tính độ dài \(AC:\) \(A{C^2} = A{B^2} + B{C^2} – 2AB.BC.\cos B\)

– Tính \(\widehat {CAB}\) dựa vào định lý sin \(\frac{{CB}}{{\sin CAB}} = \frac{{AC}}{{\sin ABC}}\)

– Tính góc AC chếch về hương tây

Lời giải chi tiết

Ta có: \(\widehat B = \left( {{{90}^ \circ } – {{36}^ \circ }} \right) + \left( {{{90}^ \circ } – {{24}^ \circ }} \right) = {120^ \circ }.\)

a) Độ dài đoạn thẳng AC là:

Áp dụng định lý cosin, ta có:

\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} – 2AB.BC.\cos B\\A{C^2} = {50^2} + {130^2} – 2.50.130.\cos {120^ \circ }\\A{C^2} = 2500 + 16900 + 6500 = 25900\\ \Rightarrow \,\,AC = \sqrt {25900}  = 10\sqrt {259}  \approx 161\,\,km\end{array}\)

b) Áp dụng định lý sin, ta có:

\(\begin{array}{l}\frac{{CB}}{{\sin CAB}} = \frac{{AC}}{{\sin ABC}}\,\, \Rightarrow \,\,\frac{{130}}{{\sin CAB}} = \frac{{161}}{{\sin {{120}^ \circ }}}\\ \Rightarrow \,\,\sin CAB = \frac{{130.\sin {{120}^ \circ }}}{{161}} \approx 0,6993\\ \Rightarrow \,\,\widehat {CAB} \approx {44^ \circ }\end{array}\)

Góc AC chếch về hướng tây một góc \({44^ \circ } – {24^ \circ } = {20^ \circ }.\)

Vậy hướng từ A đến C là: \(N{20^ \circ }W\)

============

Thuộc chủ đề:Giải sách bài tập toán 10 – Kết nối