Giải bài 3.14 trang 39 SBT Toán 10 – KN

Giải bài 3.14 trang 39 SBT Toán 10 – KN – KẾT NỐI TRI THỨC
CỦA BÀI HỌC: Bài 6. Hệ thức lượng trong tam giác – SBT Toán 10 KNTT

=======

Đề bài

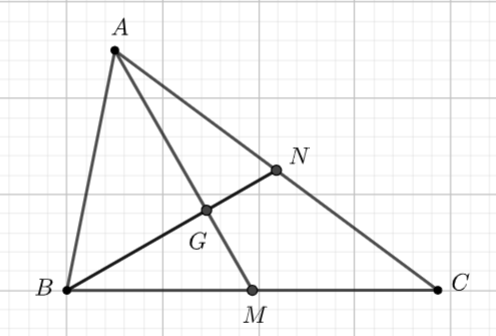
Cho tam giác \(ABC\) có hai trung tuyến kẻ từ \(A\) và \(B\) vuông góc. Chứng minh rằng:

a) \({a^2} + {b^2} = 5{c^2}.\)

b) \(\cot C = 2\left( {\cot A + cotB} \right).\)

Phương pháp giải

– Sử dụng định lý Pi-ta-go để tính \({c^2}\) và tích chất trọng tâm

– Áp dụng tính chất đường trung tuyến của tam giác

–  Sử dụng định lý cosin và diện tích của tam giác

Lời giải chi tiết

a)      \({a^2} + {b^2} = 5{c^2}.\)

Xét \(\Delta AGB\) vuông tại \(G\) có:

\(\begin{array}{l}{c^2} = A{B^2} = A{G^2} + B{G^2}\\{c^2} = {\left( {\frac{2}{3}AM} \right)^2} + {\left( {\frac{2}{3}BN} \right)^2}\\{c^2} = \frac{4}{9}\left( {\frac{{{b^2} + {c^2}}}{2} – \frac{{{a^2}}}{4}} \right) + \frac{4}{9}\left( {\frac{{{a^2} + {c^2}}}{2} – \frac{{{b^2}}}{4}} \right)\\{c^2} = \frac{4}{9}\left( {\frac{{{a^2} + {b^2} + 2{c^2}}}{2} – \frac{{{a^2} + {b^2}}}{4}} \right)\\{c^2} = \frac{4}{9}.\frac{{{a^2} + {b^2} + 4{c^2}}}{4}\\ \Leftrightarrow \,\,9{c^2} = {a^2} + {b^2} + 4{c^2}\\ \Leftrightarrow \,\,{a^2} + {b^2} = 5{c^2}\,\,\left( {dpcm} \right)\end{array}\)

b)     \(\cot C = 2\left( {\cot A + cotB} \right).\)

\(\begin{array}{l}\cot C = \frac{{\cos C}}{{\sin C}} = \frac{{\frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}}}{{\frac{{2S}}{{ab}}}} = \frac{{{a^2} + {b^2} – {c^2}}}{{4S}} = \frac{{{c^2}}}{S}\\2\left( {\cot A + \cot B} \right) = 2\left( {\frac{{\cos A}}{{\sin A}} + \frac{{\cos B}}{{\sin B}}} \right) = 2\left( {\frac{{{b^2} + {c^2} – {a^2}}}{{4S}} + \frac{{{a^2} + {c^2} – {b^2}}}{{4S}}} \right) = \frac{{2.2{c^2}}}{{4S}} = \frac{{{c^2}}}{{S}}\\ \Rightarrow \,\,\cot C = 2\left( {\cot A + \cot B} \right)\,\,\left( {dpcm} \right)\end{array}\)

 

============

Thuộc chủ đề:Giải sách bài tập toán 10 – Kết nối