Giải bài tập Ôn chương 8 (Chân trời)

Giải bài tập Ôn chương 8 (Chân trời)
========

Giải bài 1 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2

Phương pháp giải

a) Sử dụng tổ hợp, chọn 1 bạn từ 15 bạn học sinh

b) Chọn 3 bạn. Trong đó, mỗi lớp 1 bạn học sinh

c) Sử dụng quy tắc cộng và quy tắc nhân

Lời giải chi tiết

a) Số cách chọn 1 bạn từ nhóm 15 bạn là tổ hợp chập 1 của 15 \(C_{15}^1 = 15\) cách

b) Việc chọn 3 thành viên của nhóm đang học ở ba lớp khác nhau gồm 3 công đoạn:

Công đoạn 1: Chọn 1 bạn từ lớp 10A có 4 cách

Công đoạn 2: Chọn 1 bạn từ lớp 10B có 5 cách

Công đoạn 3: Chọn 1 bạn từ lớp 10C có 6 cách

Áp dụng quy tắc nhân, ta có \(4.5.6 = 120\) cách chọn 3 thành viên của nhóm đang học ở ba lớp khác nhau

c) Việc chọn 2 thành viên của nhóm đang học ở hai lớp khác nhau có 3 trường hợp:

TH1: 2 bạn đang học ở lớp 10A và 10B có \(4.5 = 20\) cách

TH2: 2 bạn đang học ở lớp 10A và 10C có \(4.6 = 24\) cách

TH3: 2 bạn đang học ở lớp 10C và 10B có \(6.5 = 30\) cách

Áp dụng quy tắc cộng, ta có \(20 + 24 + 30 = 74\) cách chọn 2 thành viên của nhóm đang học ở hai lớp khác nhau

Giải bài 2 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2

Phương pháp giải

Xác định số cách chọn 1 chữ số cho mật mã

Lời giải chi tiết

Mỗi cách chọn 1 chữ số cho mật mã là 1 trong 10 cách chọn các chữ số từ 0 đến 9. Vậy có tổng cả 10 cách chọn cho mỗi chữ số

Dãy mật mã có 3 chữ số nên có \({10^3}\) cách chọn mật mã cho khóa

Giải bài 3 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2

Phương pháp giải

Mỗi cách lây k phần tử của A và sắp xếp chúng theo một thứ tự gọi là một cchỉnh hợp chập k của n phần tử đó.

Kí hiệu \(A_n^k\) là số chỉnh hợp chập k của n phần tử.

Số các chỉnh hợp chập k của n phân tử \(1 \le k \le n\) bằng

\(A_n^k = n\left( {n – 1} \right)\left( {n – 2} \right)…\left( {n – k + 1} \right) = \frac{{n!}}{{\left( {n – k} \right)!}}\).

Lời giải chi tiết

a) Mỗi số tự nhiên có 6 chữ số được tạo ra từ 6 thẻ số trên là mỗi cách sắp xếp 6 tấm thẻ số

Vậy có \(6!\) số tự nhiên có 6 chữ số được tạo thành từ 6 tấm thẻ số đã cho

b) Để số tạo thành là số lẻ thì chữ số tận cùng là chữ số lẻ (1, 3, 5) có 3 cách chọn

Sắp xếp 5 chữ số còn lại có \(5!\) cách

Áp dụng quy tắc nhân, ta có \(3.5!\) số lẻ có 6 chữ số được tạo thành từ 6 tấm thẻ số

c) Mỗi số tự nhiên có 5 chữ số được tạo thành từ 6 thẻ số là mỗi cách chọn 5 tấm thẻ và sắp xếp chúng.

Vậy có \(A_6^5\) số có 5 chữ số được tạo thành từ 6 thẻ số đã cho

d) Để số tạo thành lớn hơn 50 000 thì chữ số đầu tiên phải là 6 hoặc 5

Sắp xếp 4 chữ số còn lại có \(A_5^4\) cách

Vậy có \(2.A_5^4\) số có 5 chữ số được tạo ra từ 6 thẻ số đã cho và lớn hơn 50 000

Giải bài 4 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2

Phương pháp giải

Cho tập hợp A có n phân tử (\(n \ge 1\))

Mỗi tập con gồm k phần tử (\(1 \le k \le n\)) của A được gọi là một tổ hợp chập k của n phân tử.

Số các tổ hợp chập k của n phần tử \(1 \le k \le n\) bằng

\(C_n^k = \frac{{n!}}{{k!\left( {n – k} \right)!}}\)

Lời giải chi tiết

Để chọn được bữa cơm đủ món theo yêu cầu cần thực hiện 3 công đoạn

Công đoạn 1: Chọn 2 món mặn từ 6 món mặn có \(C_6^2\) cách

Công đoạn 2: Chọn 2 món rau từ 5 món có \(C_5^2\) cách

Công đoạn 3: Chọn 1 món canh từ 3 món canh có 3 cách

Áp dụng quy tắc nhân, ta có \(3.C_5^2.C_6^2 = 450\) cách chọn bữa cơm gồm cơm, 2 món mặn, 2 món rau và 1 món canh

Giải bài 5 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2

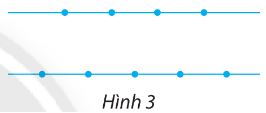
Phương pháp giải

Tam giác được tạo thành từ 3 điểm không thẳng hàng

=> chọn 2 điểm ở đường này và 1 điểm ở đường kia.

Lời giải chi tiết

Cách 1:

TH 1: Chọn 2 điểm thuộc đường thẳng có 4 điểm

Chọn 2 điểm từ đường thẳng trên có \(C_4^2\) cách

Chọn 1 điểm từ đường thẳng còn lại có 5 cách

=> Số tam giác tạo thành là \(5.C_4^2 = 30\)

TH 2: Chọn 2 điểm thuộc đường thẳng có 5 điểm

Chọn 2 điểm từ đường thẳng dưới có \(C_5^2\) cách

Chọn 1 điểm từ đường thẳng còn lại có 4 cách

=> Số tam giác tạo thành là \(4.C_5^2 = 40\)

Vậy có tất cả 70 tam giác được tạo thành.

Cách 2: 

Số cách chọn 3 điểm bất kì là:  \(C_9^3 = 84\) cách

Số cách chọn 3 điểm thẳng hàng là: \(C_4^3 +C_5^3 =14 \) cách

=> Số cách chọn 3 điểm không thẳng hàng là: 84 – 14 = 70 (cách)

Do đó ta có thể có 70 tam giác.

Giải bài 6 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2

Phương pháp giải

Áp dụng công thức nhị thức Newton \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n – k}}{b^k}} \)

Lời giải chi tiết

a) Áp dụng công thức nhị thức Newton, ta có:

\(\begin{array}{l}{\left( {a – \frac{b}{2}} \right)^4} = {a^4} + C_4^1.{a^3}\left( { – \frac{b}{2}} \right) + C_4^2.{a^2}{\left( { – \frac{b}{2}} \right)^2} + C_4^3.a{\left( { – \frac{b}{2}} \right)^3} + C_4^4.{\left( { – \frac{b}{2}} \right)^4}\\ = {a^4} – 2{a^3}b + \frac{3}{2}{a^2}{b^2} – \frac{1}{2}a{b^3} + \frac{1}{16}{b^4}\end{array}\)

b) Áp dụng công thức nhị thức Newton, ta có:

\(\begin{array}{l}{\left( {2{x^2} + 1} \right)^5} = {\left( {2{x^2}} \right)^5} + C_5^1.{\left( {2{x^2}} \right)^4}.1 + C_5^2.{\left( {2{x^2}} \right)^3}{.1^2} + C_5^3.{\left( {2{x^2}} \right)^2}{.1^3} + C_5^4.\left( {2{x^2}} \right){.1^4} + {1^5}\\ = 32{x^{10}} + 80{x^8} + 80{x^6} + 40{x^4} + 10{x^2} + 1\end{array}\)

Giải bài 7 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2

Phương pháp giải

Áp dụng công thức nhị thức Newton \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n – k}}{b^k}} \)

Lời giải chi tiết

a) Áp dụng công thức nhị thức Newton, ta có:

\(\begin{array}{l}{\left( {1 + x} \right)^4} = {1^4} + C_4^1{.1^3}x + C_4^2{.1^2}{x^2} + C_4^3.1{x^3} + C_4^4{x^4}\\ = 1 + 4x + 6{x^2} + 4{x^3} + {x^4}\end{array}\)

\(\begin{array}{l}{\left( {1 – x} \right)^4} = {1^4} + C_4^1{.1^3}\left( { – x} \right) + C_4^2{.1^2}{\left( { – x} \right)^2} + C_4^3.1{\left( { – x} \right)^3} + C_4^4{\left( { – x} \right)^4}\\ = 1 – 4x + 6{x^2} – 4{x^3} + {x^4}\end{array}\)

Suy ra

\(\begin{array}{l}{\left( {1 + x} \right)^4} + {\left( {1 – x} \right)^4} = 1 + 4x + 6{x^2} + 4{x^3} + {x^4} + 1 – 4x + 6{x^2} – 4{x^3} + {x^4}\\ = 2 + 12{x^2} + 2{x^4}\end{array}\)

Vậy \({\left( {1 + x} \right)^4} + {\left( {1 – x} \right)^4} = 2 + 12{x^2} + 2{x^4}\)

Ta có: \(1,{05^4} + 0,{95^4} = {\left( {1 + 0,5} \right)^4} + {\left( {1 – 0,5} \right)^4}\)

Áp dụng biểu thức vừa chứng minh \({\left( {1 + x} \right)^4} + {\left( {1 – x} \right)^4} = 2 + 12{x^2} + 2{x^4}\) ta có:

\(\begin{array}{l}1,{05^4} + 0,{95^4} = {\left( {1 + 0,5} \right)^4} + {\left( {1 – 0,5} \right)^4} = 2 + 12.0,{5^2} + 2.0,{5^4}\\ = 5,125\end{array}\)