Giải bài tập Bài 3: Phương trình quy về bậc hai (Chân trời)

Giải bài tập Bài 3: Phương trình quy về bậc hai (Chân trời)

=========

Giải bài 1 trang 17 SGK Toán 10 Chân trời sáng tạo tập 2

Giải các phương trình sau:

a) \(\sqrt {11{x^2} – 14x – 12}  = \sqrt {3{x^2} + 4x – 7} \)

b) \(\sqrt {{x^2} + x – 42}  = \sqrt {2x – 30} \)

c) \(2\sqrt {{x^2} – x – 1}  = \sqrt {{x^2} + 2x + 5} \)

d) \(3\sqrt {{x^2} + x – 1}  – \sqrt {7{x^2} + 2x – 5}  = 0\)

Phương pháp giải

Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn

Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn

Bước 3: Giải phương trình nhận được ở bước 2

Bước 4: Thử lại nghiệm và kết luận

Lời giải chi tiết

a) \(\sqrt {11{x^2} – 14x – 12}  = \sqrt {3{x^2} + 4x – 7} \)

\(\begin{array}{l} \Rightarrow 11{x^2} – 14x – 12 = 3{x^2} + 4x – 7\\ \Rightarrow 8{x^2} – 18x – 5 = 0\end{array}\)

\( \Rightarrow x =  – \frac{1}{4}\) và \(x = \frac{5}{2}\)

Thay nghiệm vừa tìm được vào phương trình \(\sqrt {11{x^2} – 14x – 12}  = \sqrt {3{x^2} + 4x – 7} \) ta thấy chỉ có nghiệm \(x = \frac{5}{2}\) thảo mãn phương trình

Vậy nhiệm của phương trình đã cho là \(x = \frac{5}{2}\)

b) \(\sqrt {{x^2} + x – 42}  = \sqrt {2x – 30} \)

\(\begin{array}{l} \Rightarrow {x^2} + x – 42 = 2x – 3\\ \Rightarrow {x^2} – x – 12 = 0\end{array}\)

\( \Rightarrow x =  – 3\) và \(x = 4\)

Thay vào phương trình \(\sqrt {{x^2} + x – 42}  = \sqrt {2x – 30} \)  ta thấy  không có nghiệm nào thỏa mãn

Vậy phương trình đã cho vô nghiệm

c) \(2\sqrt {{x^2} – x – 1}  = \sqrt {{x^2} + 2x + 5} \)

\(\begin{array}{l} \Rightarrow 4.\left( {{x^2} – x – 1} \right) = {x^2} + 2x + 5\\ \Rightarrow 3{x^2} – 6x – 9 = 0\end{array}\)

\( \Rightarrow x =  – 1\) và \(x = 3\)

Thay hai nghiệm trên vào phương trình \(2\sqrt {{x^2} – x – 1}  = \sqrt {{x^2} + 2x + 5} \) ta thấy cả hai nghiệm đếu thỏa mãn phương trình

Vậy nghiệm của phương trình \(2\sqrt {{x^2} – x – 1}  = \sqrt {{x^2} + 2x + 5} \) là \(x =  – 1\) và \(x = 3\)

d) \(3\sqrt {{x^2} + x – 1}  – \sqrt {7{x^2} + 2x – 5}  = 0\)

\(\begin{array}{l} \Rightarrow 3\sqrt {{x^2} + x – 1}  = \sqrt {7{x^2} + 2x – 5} \\ \Rightarrow 9.\left( {{x^2} + x – 1} \right) = 7{x^2} + 2x – 5\\ \Rightarrow 2{x^2} + 7x – 4 = 0\end{array}\)

\( \Rightarrow x =  – 4\) và \(x = \frac{1}{2}\)

Thay hai nghiệm trên vào phương trình \(3\sqrt {{x^2} + x – 1}  – \sqrt {7{x^2} + 2x – 5}  = 0\) ta thấy chỉ có nghiệm \(x =  – 4\) thỏa mãn phương trình 

Vậy nghiệm của phương trình trên là \(x =  – 4\)

Giải bài 2 trang 17 SGK Toán 10 Chân trời sáng tạo tập 2

Giải các phương trình sau:

a) \(\sqrt {{x^2} + 3x + 1}  = 3\)

b) \(\sqrt {{x^2} – x – 4}  = x + 2\)

c) \(2 + \sqrt {12 – 2x}  = x\)

d) \(\sqrt {2{x^2} – 3x – 10}  =  – 5\)

Phương pháp giải

Bước 1: Chuyển biểu thức có căn về một vế

Bước 2: Bình phương hai vế của phương trình để làm mất dấu căn

Bước 3: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn

Bước 4: Giải phương trình nhận được ở bước 2

Bước 5: Thử lại nghiệm và kết luận

Lời giải chi tiết

a) \(\sqrt {{x^2} + 3x + 1}  = 3\)

\(\begin{array}{l} \Rightarrow {x^2} + 3x + 1 = 9\\ \Rightarrow {x^2} + 3x – 8 = 0\end{array}\)

\( \Rightarrow x = \frac{{ – 3 – \sqrt {41} }}{2}\) và \(x = \frac{{ – 3 + \sqrt {41} }}{2}\)

Thay hai nghiệm trên vào phương trình \(\sqrt {{x^2} + 3x + 1}  = 3\) ta thấy cả hai nghiệm đều thỏa mãn phương trình

Vậy nghiệm của phương trình đã cho là \(x = \frac{{ – 3 – \sqrt {41} }}{2}\) và \(x = \frac{{ – 3 + \sqrt {41} }}{2}\)

b) \(\sqrt {{x^2} – x – 4}  = x + 2\)

\(\begin{array}{l} \Rightarrow {x^2} – x – 4 = {\left( {x + 2} \right)^2}\\ \Rightarrow {x^2} – x – 4 = {x^2} + 4x + 4\\ \Rightarrow 5x =  – 8\\ \Rightarrow x =  – \frac{8}{5}\end{array}\)

Thay \(x =  – \frac{8}{5}\) và phương trình \(\sqrt {{x^2} – x – 4}  = x + 2\) ta thấy thỏa mãn phương trình

Vậy nghiệm của phương trình đã cho là \(x =  – \frac{8}{5}\)

c) \(2 + \sqrt {12 – 2x}  = x\)

\(\begin{array}{l} \Rightarrow \sqrt {12 – 2x}  = x – 2\\ \Rightarrow 12 – 2x = {\left( {x – 2} \right)^2}\\ \Rightarrow 12 – 2x = {x^2} – 4x + 4\\ \Rightarrow {x^2} – 2x – 8 = 0\end{array}\)

\( \Rightarrow x =  – 2\) và \(x = 4\)

Thay hai nghiệm vừa tìm được vào phương trình \(2 + \sqrt {12 – 2x}  = x\) thì thấy chỉ có \(x = 4\) thỏa mãn

Vậy \(x = 4\) là nghiệm của phương trình đã cho.

d) Ta có biểu thức căn bậc hai luôn không âm nên \(\sqrt {2{x^2} – 3x – 10}  \ge 0\forall x \in \mathbb{R}\)

\( \Rightarrow \sqrt {2{x^2} – 3x – 10}  =  – 5\) (vô lí)

Vậy phương trình đã cho vô nghiệm

Giải bài 3 trang 17 SGK Toán 10 Chân trời sáng tạo tập 2

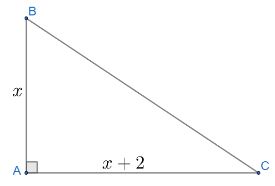
Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2 cm.

a) Biểu diễn độ dài cạnh huyền BC theo AB

b) Biết chu vi của tam giác ABC là 24 cm. Tính độ dài ba cạnh của tam giác đó.

Phương pháp giải

a) Bước 1: Đặt độ dài cạnh AB là x (\(x > 0\)), biểu diễn AC theo AB

Bước 2: Áp dụng định lý Pitago biểu diễn cạnh BC

b) Bước 1: Lập biểu thức tính chu vi của tam giác

Bước 2: Giải phương trình vừa tìm được

Lời giải chi tiết

a) Đặt độ dài cạnh AB là x (\(x > 0\))

Theo giả thiết ta có độ dài \(AC = AB + 2 = x + 2\)

Áp dụng định lý pitago trong tam giác vuông ta có

\(BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{x^2} + {{\left( {x + 2} \right)}^2}}  = \sqrt {2{x^2} + 4x + 4} \)

b) Chu vi của tam giác là \(C = AB + AC + BC\)

\( \Rightarrow C = x + \left( {x + 2} \right) + \sqrt {2{x^2} + 4x + 4}  = 2x + 2 + \sqrt {2{x^2} + 4x + 4} \)

Theo giả thiết ta có

\(\begin{array}{l}C = 24 \Leftrightarrow 2x + 2 + \sqrt {2{x^2} + 4x + 4}  = 24\\ \Leftrightarrow \sqrt {2{x^2} + 4x + 4}  = 22 – 2x\\ \Rightarrow 2{x^2} + 4x + 4 = {\left( {22 – 2x} \right)^2}\\ \Rightarrow 2{x^2} + 4x + 4 = 4{x^2} – 88x + 484\\ \Rightarrow 2{x^2} – 92x + 480 = 0\end{array}\)

\( \Rightarrow x = 6\) hoặc \(x = 40\)

Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} + 4x + 4}  = 22 – 2x\) ta thấy chỉ có  \(x = 6\) thỏa mãn phương trình

Vậy độ dài ba cạnh của tam giác là \(AB = 6;AC = 8\) và \(BC = 10\)(cm)

Giải bài 4 trang 17 SGK Toán 10 Chân trời sáng tạo tập 2

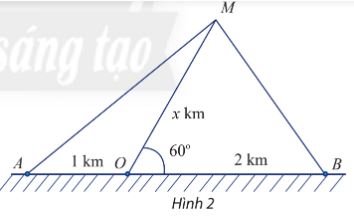
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc \(60^\circ \). Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng 1km và 2km (Hình 2).

a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.

b) Tìm x để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A

c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.

Lưu ý: Làm tròn kết quả đến hàng phần trăm. 

Phương pháp giải

a) Sử dụng định lý cosin \({a^2} = {b^2} + {c^2} + 2bc\cos A\)

b) Lập phương trình \(MB = \frac{4}{5}MA\), và giải phương trình lập được

c) Lập phương trình \(MB = MO – 0,5\), và giải phương trình lập được

Lời giải chi tiết

a) Đặt độ dài của MO là x km \(\left( {x > 0} \right)\)

Ta có: \(\widehat {MOA} + \widehat {MOB} = 180^\circ \) (hai góc bù nhau) \( \Rightarrow \widehat {MOA} = 120^\circ \)

Áp dụng định lý Cosin trong tam giác ta tính được:

+) Khoảng cách từ tàu đến B là \(MB = \sqrt {{x^2} + {2^2} – 2.2.x.\cos 60^\circ }  = \sqrt {{x^2} – 2x + 4} \)

+) Khoảng cách từ tàu đến A là \(MA = \sqrt {{x^2} + {1^2} – 2.1.x.\cos 120^\circ }  = \sqrt {{x^2} + x + 1} \)

b) Theo giải thiết ta có phương trình \(MB = \frac{4}{5}MA \Rightarrow \sqrt {{x^2} – 2x + 4}  = \frac{4}{5}\sqrt {{x^2} + x + 1} \)

\(\begin{array}{l} \Rightarrow {x^2} – 2x + 4 = \frac{{16}}{{25}}\left( {{x^2} + x + 1} \right)\\ \Rightarrow \frac{9}{{25}}{x^2} – \frac{{66}}{{25}}x + \frac{{84}}{{25}} = 0\end{array}\)

\( \Rightarrow x \simeq 1,64\) và \(x \simeq 5,69\)

Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {{x^2} – 2x + 4}  = \frac{4}{5}\sqrt {{x^2} + x + 1} \) ta thấy cả hai nghiệm đều thỏa mãn phương trình

Vậy khi  \(x \simeq 1,64\) hoặc \(x \simeq 5,69\) thì khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A

c) Đổi 500 m = 0,5 km

Theo giả thiết ta có phương trình sau:

\(\begin{array}{l}MB = MO – 0,5 \Rightarrow \sqrt {{x^2} – 2x + 4}  = x – 0,5\\ \Rightarrow {x^2} – 2x + 4 = {\left( {x – 0,5} \right)^2}\\ \Rightarrow {x^2} – 2x + 4 = {x^2} – x + \frac{1}{4}\\ \Rightarrow x = \frac{{15}}{4}\end{array}\)

Thay \(x = \frac{{15}}{4}\) vào phương trình \(\sqrt {{x^2} – 2x + 4}  = x – 0,5\) ta thấy thỏa mãn phương trình

Vậy khi \(x = \frac{{15}}{4}\) thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.